
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад розв’язку завдання 3 ⇐ ПредыдущаяСтр 6 из 6
А. Виробництво продовольчих товарів в Україні
Середнє значення рівня ряду:
n – число рівнів ряду.
Таблиця 6.3.5 Показники аналізу ряду динаміки, обчислені ланцюговим і базисним методом
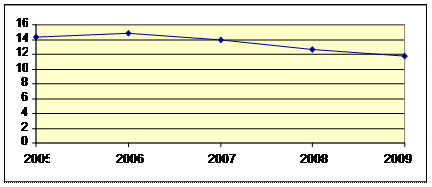
Динаміку виробництва умовної продукції Ж7 представимо графічно:
Рис.6.3.2. Графічне зображення динаміки виробництва продукції Ж7.
Таблиця 6.3.6 (Б) Дані про витрати на рекламу підприємства „Авіс”
На основі даних підприємств про витрати на рекламу за три роки проведемо аналіз сезонних коливань витрат на рекламу трьома методами: 1. Середньої арифметичної. Полягає в обчисленні середніх за збільшеними інтервалами. 2. Плинної середньої. Полягає в обчисленні середніх за збільшеними інтервалами при поступовому переміщенні інтервалу на один крок. 3. Методом аналітичного вирівнювання. Вирівнювання здійснюється за рівнянням прямої. Таблиця 6.3.7 Вирівнювання динамічного ряду
Параметри рівняння прямої визначаємо методом найменших квадратів за допомогою системи рівнянь.
Звідси:
Поступово підставляючи в рівняння прямої значення порядкового номеру періода, ми отримали новий вирівняний ряд значень.
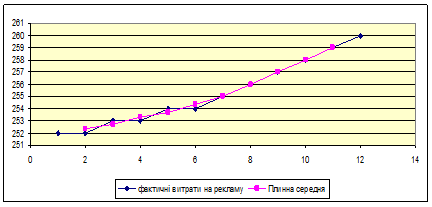
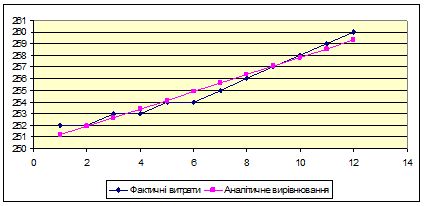
Представимо графічно отримані ряди:
Рис. 6.3.3. Плинна середня.
Рис. 6.3.4. Середня арифметична
Рис. 6.3.5. Аналітичне вирівнювання
Виявити і виміряти ступінь сезонних коливань можна за допомогою індекса сезонності:
Аналіз сезонних коливань витрат на рекламу за допомогою індекса сезонності представлено в наступній таблиці.
Таблиця 6.3.8 Аналіз сезонних коливань
Визначаємо середні витрати на рекламу для кожного року: Базовий (252+252+253+253)/4=252,5 Минулий (254+254+255+256)/4=254,75 Звітний (257+258+259+260)/4=258,5
Рис.6.3.6 Сезонна хвиля
Для розрахунків характеристик сезонності побудуємо допоміжну таблицю.
Таблиця 6.3.9 Дані для обчислення характеристик сезонності
Сезонне значення індекса сезонності:
І = 12,000/12 = 1 Узагальнюючі характеристики сезонних коливань: Амплітуда коливань: Середнє лінійне відхилення:
Середнє квадратичне відхилення: Дисперсія сезонних коливань:
Коефіцієнт варіації:
Висновок: На графіку динамічного ряду видно, що протягом 2005-2006 років обсяги випуску продукції Ж7 збільшився, а починаючи із 2006 року почав зменшуватися. На графіку витрат на рекламу можна побачити, що витрати на рекламу значно зросли за звітний період. Методичні рекомендації до завдання 4 Та приклад розв’язку Статистичний індекс – це узагальнюючий показник порівняння двох сукупностей, що складаються з елементів, які не підлягають безпосередньому підсумовуванню. Розраховуються індекси для характеристики зміни обсягів виробленої, реалізованої чи спожитої продукції в натурально–речовій формі; зміни загального рівня цін, собівартості виробництва продукції, продуктивності праці, врожайності та ін. Як відносні показники можуть виражатися у вигляді коефіцієнтів (якщо базовий рівень приймати за 1) або у вигляді процентів (коли він прийнятий за 100). Коли індекс більше 1 (або 100%), то рівень індексного явища, яке вивчається, зростає, а якщо менше 1 (або 100%) – знижується. Статистичні індекси класифікують за рядом ознак.
Класифікація індексів
1. Індивідуальні
2. Зведені
Зведені в свою чергу поділяються на 1. Індекси кількісних показників (з вагами базисного періоду). Наприклад індекси фізичного обсягу, розміру і структури посівів, чисельності та ін.
Основні умовні позначення показників, зміна яких може бути визначена за допомогою індексів:
0 – показники базисного періоду; 1 – показник поточного періоду; q – кількість виробленої, реалізованої чи спожитої продукції певного виду в натуральному вираженні; р – ціна одиниці товару чи продукції; z – собівартість одиниці продукції; t – трудомісткість продукції; у – урожайність певної культури; n – розмір посівної площі; рq – товарообіг або вартість виготовленої продукції; zq – загальна собівартість продукції певного виду, тобто витрати на її виробництво; tq – загальні витрати робочого часу (праці) на виробництво певного виду продукції; yn – валовий збір певної сільськогосподарської культури. Індивідуальні індекси (і) дають порівняльну характеристику окремих елементів тієї чи іншої сукупності. Зведені індекси позначаються буквою І і порядковий знак вказує на показник, зміну якого характеризує даний індекс. При розрахунку зведеного індексу, перш за все, додається несумарність елементів явища, що вивчається. Це досягається шляхом введення в індекс деякого додаткового і, при тому, незмінного показника, економічно тісно пов’язаного з індексованим показником. Окремі показники утворюються в результаті множення двох і більше показників (вартість виробленої продукції дорівнює добутку витрат праці на їх продуктивність і ін.).
Тому і зміна складних економічних явищ відбувається під впливом окремих факторів (співмножників). Так, наприклад, зміна товарообороту може бути викликана як зміною цін на окремі товари, так і зміною кількості реалізованих товарів. В кожному конкретному випадку необхідно визначити зміст фактора-співмножника. Як правило,один фактор, а саме якісний, виступає як інтенсивний (продуктивність, ціна, собівартість і т.д.), а другий, а саме об’єктивний, - як екстенсивний (витрати праці, кількість продукції і т.д.). Для вивчення впливу одного з факторів-співмножників на зміну явища, інші залишають умовно незмінним фіксованими на рівні одного з періодів. Якщо незмінними є екстенсивний показник, то він виступає в ролі вагів, а якщо інтенсивний – то в ролі сумірника. Правило: Інтенсивні фактори-співмножники фіксуються на рівні базисного періоду, а екстенсивний – на рівні поточного. Якщо позначити через х – інтенсивний фактор, а через у екстенсивний то розрахункові формули матимуть вигляд:
Іх – зведений індекс інтенсивного показника; Іу – зведений індекс екстенсивного показника; Іху – індекс зміни явища за рахунок впливу двох факторів одночасно. Така форма побудови зведених індексів називається агрегатною, тобто це відносна зміна індексованого показника. Між вище наведеними індексами існує зв’язок:
Оцінка абсолютної зміни індексованого показника, може відображатися так: загальний абсолютний приріст показника який вивчається, визначається таким чином
При цьому абсолютний приріст за рахунок інтенсивного фактора становитиме
А приріст за рахунок екстенсивного фактора становитиме
Тобто
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.111.9 (0.064 с.) |
 , де:
, де: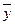 – досліджувані рівні динамічного ряду;
– досліджувані рівні динамічного ряду;
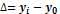

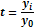
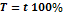 -ланцюговий
-ланцюговий
 -ланцюговий
-ланцюговий
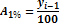
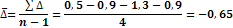
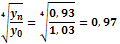



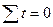
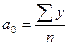
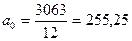

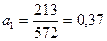
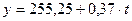

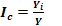

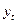


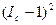
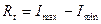 = 1,006-0,994 = 0,012
= 1,006-0,994 = 0,012 = 0,036/12 = 0,003
= 0,036/12 = 0,003
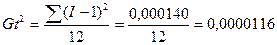
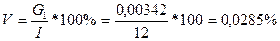
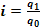 (6.40)
(6.40)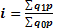 (6.41)
(6.41)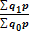 ;
;  і ін. (6.42)
і ін. (6.42)
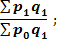
 і ін. (6.43)
і ін. (6.43)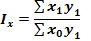 (6.44)
(6.44)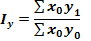 (6.45)
(6.45)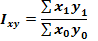 (6.46)
(6.46) (6.47)
(6.47)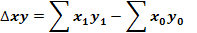 (6.48)
(6.48)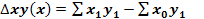 (6.49)
(6.49)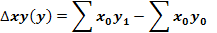 (6.50)
(6.50)



