
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие методические указания к решению задачи 9Содержание книги
Поиск на нашем сайте
По пункту 1. Статистические характеристики –
а)
где
i – величина интервала; А – условно заданная величина не равная 0; б) где
в) среднеквадратическое отклонение s определяется посредством извлечения корня квадратного из дисперсии Ниже для иллюстрации приводится последовательность расчетов и полученные результаты, выполненные по индивидуальным данным информационной базовой табл. 22. Примем А = 7500; i = 1000. Таблица 22 Промежуточная таблица
Таким образом,
и далее
где М1 – центральный момент 1-го порядка; М2 – центральный момент
При проведении расчетов по групповым данным имеем: А = 7672,00 Таблица 23
S = 1……K; K – число групп,
Согласно приведенным формулам получаем:
Не трудно видеть, что средние величины, рассчитанные по индивидуальным и групповым данным полностью совпали между собой. Между дисперсиями имеется незначительное различие. В общем случае систематическая ошибка в дисперсии или ошибка Ф. Шепарда составляет 1/12 квадрата величины интервала, т. е. скорректированная дисперсия σ = (1/12) i2. Ее применение, однако, допустимо при определенных условиях: а) группировка должна формироваться на основе большого числа наблюдений (n > 500); б) характеризоваться тесной близостью с осью абсцисс на концах кривой. По пункту 2 в интервальном вариационном ряду М0, Ме ДКД рассчитываются по следующей формуле:
где М0 – мода, наиболее часто повторяющееся значение признака; X
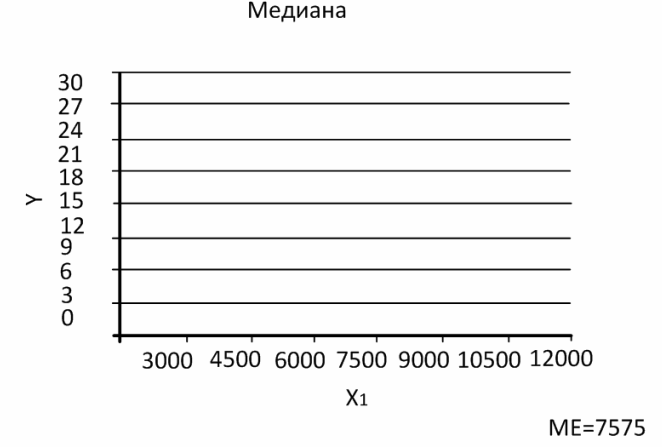
где Ме – медиана, серединное значение признака; Х Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является во всех случаях модальным и его вершины соединяются с вершинами предшествующего и последующего прямоугольников. Абсцисса точек пересечения этих прямых и будет модой ряда распределения. Медиана рассчитывается по кумуляте. Для чего из точки на шкале постоянных частот, соответствующей 50 %, проводится прямая параллельная оси абсцисс до пересечения с асимптотой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс и медиана определена
ДКД = где ДКД – децильный коэффициент дифференциации; Дециль в общем случае делит ранжированный ряд на 10 равных частей. 1-я дециль делит ряд в соотношении 1 и 9, 2-я дециль = 2 и 8 и т. д., 1-я дециль – это значение признака Х1 – которое отсекает 10 % единиц наблюдения, имеющих наименьшие численные значения признака. 9-я дециль – это значение признака Х1, которое отсекает 10 % единиц наблюдения, имеющих наибольшие численные значения признака. Расчеты децилей производятся по формулам медианы, с учетом того, что совокупность делится не пополам, а на 10 равных частей в названных соотношениях
где
где Расчеты по вышеприведенным формулам не представляют каких-либо трудностей. Применительно к нашему примеру имеем следующее (табл. 24).
Таблица 24
Графически мода и медиана представляется следующим образом
Рис. 4. Мода
Рис. 5. Медиана
ДКД По пункту 3 задачи. Для сравнительного анализа степени ассиметрии изучаемого вариационного ряда рассчитывается относительный показатель ассиметрии
Величина показателя ассиметрии может быть положительной и отрицательной, что указывает на наличие правосторонней или левосторонней ассиметрии. Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна 0)
Если отношение Для симметричных распределений рассчитывается показатель эксцесса (островершинности)
Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины нормального распределения. В нормальном распределении отношение Оценки существенности показателей ассиметрии и эксцесса позволяют сделать вывод о том, что можно отнести данное эмпирическое распределение к типу кривых нормального распределения. Определение вышеназванных коэффициентов предполагает расчет условных моментов 3-го и 4-го порядка
и переход центральным моментам 3-го и 4-го порядка. Приведем используемые в статистике формулы перехода от условных моментов к центральным:
и далее
Ниже приводится последовательность расчетов и полученные результаты по пункту 3 данной задачи (табл. 25). Таблица 25
m3 = –0,5807; m4 = 9,0574 M3 = 698142919,9; M4 = 4,5341E+13; As = 0,079; E = –0,53.
Задача 10 Проанализируйте полученные результаты решения, представленные в задачах 8, 9. Примите гипотезу о нормальном распределении частот рассматриваемого вариационного ряда. Произведите его математическое выравнивание с помощью кривой нормального распределения. Рассчитайте критерии согласия Пирсона, Романовского и Колмогорова. Сопоставьте полученные результаты с их табличными значениями. Сформулируйте выводы. Изобразите на графике (совместно) эмпирический и теоретический ряды распределения (рис. 6).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.163.167 (0.01 с.) |

 ,
,  и
и  были рассчитаны обычным способом в задачах 2 (по индивидуальным данным) и 3
были рассчитаны обычным способом в задачах 2 (по индивидуальным данным) и 3 
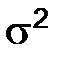

 ,
, – условный момент 1-го порядка:
– условный момент 1-го порядка: – для индивидуальных данных;
– для индивидуальных данных; – для групповых данных;
– для групповых данных;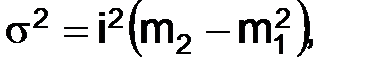
 – условный момент 2-го порядка
– условный момент 2-го порядка ;
;  ;
; .
.

 ;
;  ;
; ;
;  ;
;
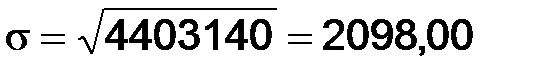 ,
,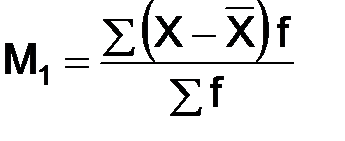 ;
;  .
.



 ;
;  .
.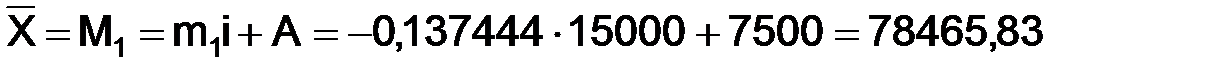 ;
; ;
; .
.
 – нижняя граница значения интервала содержащего моду; i – величина интервала;
– нижняя граница значения интервала содержащего моду; i – величина интервала;  – частота модального интервала;
– частота модального интервала;  – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;  – частота интервала, следующего за модальным
– частота интервала, следующего за модальным ,
, – нижняя граница значения интервала содержащего медиану; i – величина интервала;
– нижняя граница значения интервала содержащего медиану; i – величина интервала; – сумма частот;
– сумма частот;  – сумма накопленных частот предшествующих медианному интервалу;
– сумма накопленных частот предшествующих медианному интервалу;  – частота медианного интервала.
– частота медианного интервала.
 – 9-я дециль;
– 9-я дециль;  – 1-я дециль.
– 1-я дециль.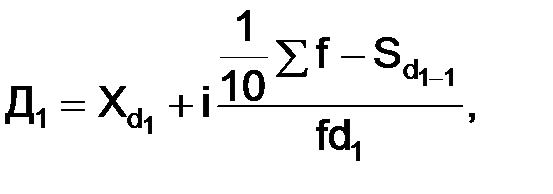
 – нижняя граница интервала группы, содержащую 1-ю дециль,
– нижняя граница интервала группы, содержащую 1-ю дециль, – сумма частот;
– сумма частот;  – накопленная сумма частот, предшествующую интервалу, содержащая 1-ю дециль;
– накопленная сумма частот, предшествующую интервалу, содержащая 1-ю дециль;  – частота интервала, содержащая 1 дециль
– частота интервала, содержащая 1 дециль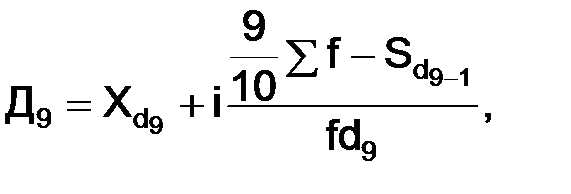
 – нижняя граница интервала группы, содержащую 9-ю дециль;
– нижняя граница интервала группы, содержащую 9-ю дециль;  – сумма частот;
– сумма частот;  – накопленная сумма частот, предшествующая интервалу, содержащую 9-ю дециль;
– накопленная сумма частот, предшествующая интервалу, содержащую 9-ю дециль;  – частота интервала, содержащую 9-ю дециль.
– частота интервала, содержащую 9-ю дециль. i = 1500;
i = 1500; 






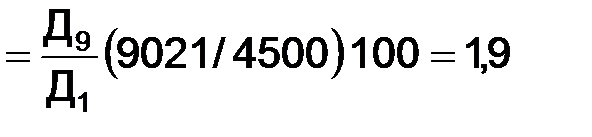 раза.
раза.

 ассиметрия существенна, если же
ассиметрия существенна, если же 


 ;
; 













