
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Висновок за аналогією має ймовірний характер.Содержание книги
Поиск на нашем сайте
Види аналогії: проста аналогія, строга аналогія, нестрога аналогія. Проста аналогія – аналогія, в якій на підставі подібності предметів за одними якими-небудь ознаками роблять висновок про їх подібність в інших ознаках. Строга аналогія – аналогія, що ґрунтується на знанні залежності ознак предметів, які порівнюються. Нестрога аналогія – аналогія, в результаті якої робиться висновок від подібності двох предметів в одних ознаках до подібності їх за такою ознакою, про зв’язок якої з першими нічого не відомо.
Питання для самоперевірки знань: 1. Чим умовиводи відрізняються від інших форм мислення? 2. Чим відрізняються безпосередні умовиводи від опосередкованих? 3. Які умовиводи називаються безпосередніми? 4. Що таке обернення? 5. Що називається протиставлення? 6. У чому полягає логічна підстава для здійснення операцій перетворення та обернення? 7. Що характерне для дедуктивних умовиводів? 8. Які визначення простого категоричного силогізму ви знаєте і в чому полягає перевага кожного з них? 9. Як встановити структуру силогізму? 10. Чому люди часто вдаються до ентимем? 11. Які види ентимем ви знаєте? 12. Який силогізм називається складним? 13. Які види полісилогізмів (складних силогізмів) ви знаєте? 14. Що таке дилема, трилема, полілема? 15. Які є види умовиводів? 16. Чим індуктивні умовиводи відрізняються від дедуктивних? 17. Які умовиводи називаються ймовірними? 18. Що характерне для повної індукції? 19. В чому полягає сутність математичної індукції? 20. Яка індукція називається неповною? 21. Що характерне для популярної індукції? 22. Яка індукція називається науковою? 23. Які ви знаєте методи встановлення причинних зв’язків між явищами? 24. Що таке аналогія? 25. Які види аналогії ви знаєте?
Вправи та задачі для контрольної перевірки знань: 1. Які з цих умовиводів безпосередні, а які опосередковані (обґрунтуйте свої твердження). а) Всі адвокати – юристи. Отже, деякі юристи – адвокати; б) Деякі батьки – спортсмени. Отже, деякі спортсмени – батьки; в) Якщо цю ділянку землі удобрювати, то вона дасть добрий урожай. Названу ділянку землі не вдобрювали. Вона гн дала доброго урожаю; г) Деякі люди – дальтоніки. Отже, деякі люди не є недальтониками; д) Відомо, що судження „Всі метали - електропровідні” – істинне. Отже, суперечне йому судження „Деякі метали не є електропровідними” – хибне; е) Всі паралелограми – чотирикутники. Отже, жоден не чотирикутник не є паралелограмом; є) Всі люди – мислячі істоти. Отже, Петренко – мисляча істота. 2. Перетворіть такі судження: а) Люди мають естетичні почуття; б) Жоден патріот не зневажає культуру свого народу; в) Деякі люди – митці; г) Деякі метали не тонуть у воді. 3. Оберніть такі судження: а) Кожна людина має право на свободу; б) Жоден гуманіст не визнає права будь-якого на приниження людської гідності особи; в) Деякі тварини – альбіноси; г) Деякі люди – інженери. 4. Чи правильно здійснено протиставлення предикатові в таких прикладах (свої твердження обґрунтуйте): а) Всі рослини – живі організми. Отже, деякі живі організми не є не рослинами; б) Жоден патріот не відмовляється від мови своєї нації. Отже, деякі з тих, хто не відмовляється від мови своєї нації, є патріотами; в) Деякі рослини не бояться посухи. Отже, деякі з тих, що не бояться посухи, є рослинами; г) Деякі вчені і тільки вчені здатні передбачати майбутнє. Отже, всі, хто здатен передбачати майбутнє, є вченими; д) Всі люди і тільки люди мають свідомість. Отже, всі, хто не має свідомості, не є людьми; е) Жодна людина не бажає загибелі життя на Землі. Отже, жоден з тих, хто бажає загибелі життя на Землі, не є людиною. 5. Поняття умовиводу, його структура і форми. 6. Правила забезпечення правильного умовиводу. 7. Категоричний силогізм, його різновиди. 8. Поняття модусів та фігур. 9. Операції перетворення, обернення та протиставлення предикату. 10. Здійснити операції перетворення, обернення та протиставлення предикату в судженні: «Всі люди смертні». 11. Зробіть (якщо це можливо) висновок з кожної пари засновків і аргументуйте власну відповідь: - Тому, хто лисий, гребінець не потрібний. Жодна ящірка не має волосся. - Картопля — не ананас. Всі ананаси приємні на смак. - Займайтесь своєю справою. Ця сварка — не ваша справа. - Жодна шпилька не має честолюбних намірів. Жодна голка не є шпилькою. - Жодна жаба не пише книжок. Деякі люди користуються чорнилом, коли пишуть книжки. - Жодна коцюба не є м'якою. Всі подушки — м'які. - Всі оси не є товариськими. Всі цуцики є товариськими. - Жодна з моїх кузин не є справедливою. Всі судді справедливі. - Всі мої кузини несправедливі. Жоден суддя не є справедливим. - Він сказав мені, що ви пішли. Він ніколи не говорив ні слова правди. Література: 1. Арутюнов В. X., Кирик Д. П., Мішин В. М. Логіка: Навч. посібник для економістів. — К.: КНЕУ, 2000. – 144 с. 2. Гетманова А.Д. Логика для юристов. – М.: Омега- Л., 2005. – 418 с. 3. Грядовой Д.И. Логика: Практический курс основ формальной логики. – М.:Щит-М, 2004 – 255с. 4. Далидов И.В. Логика: Учебник. – М.: Дащков и К, 2004. – 347 с. 5. Ивин А.А. Логика: Учебник. – М.: Гардарики, 2004. – 347 с. 6. Петровська І.Р. Логіка. – Львів: Нац. ун-т „Львів. політехніка”, 2004. – 147с. 7. Гладунский В.Н. Логіка: Навч. посібник. – Львів: Афіша, 2002. – 358 с. 8. Бандурка О.М. Курс логіки: Підручник. – К.: Літера, 2002. – 159 с. Тема 5. Закони логіки План: 1. Закон тотожності. 2. Закон суперечності. 3. Закон виключеного третього. 4. Закон достатньої підстави. 5. Закон подвійного заперечення. 6. Закон ідемпотентності. 7. Закон комутативності. 8. Закон асоціативності. 9. Закон дистрибутивності. 10. Закон де Моргана. 11. Закони контра позиції. 12. Закони складної контра позиції.
Основний зміст логіки становлять її закони: тотожності, суперечності, виключеного третього, достатньої підстави та ін. Автором перших трьох законів вважається Аристотель, автором четвертого закону – Г. –В.Лейбниц. Перші чотири закони прийнято називати основними законами на тій підставі, що вони виражають такі корінні риси логічно правильного мислення як визначеність, послідовність, несперечливість і обґрунтованість думки; відбивають найпростіші і найзагальніші відношення в явищах об’єктивної дійсності. Їх дотримання обов’язкове. Закони логіки – це внутрішній, необхідний, істотний зв’язок між думками. Закон тотожності: кожна думка має бути чіткою за обсягом, ясною за змістом і залишатися незмінною в ході одного й того ж міркування. Схема закону: А→А („Якщо А, то А”); А↔А („А тоді і тільки тоді, коли А”). Закон суперечності: два судження, в одному з яких щось стверджується, а в другому те саме, в той же час і в тому відношенні заперечується, не можуть бути одночасно істинними. Схема закону: в сучасній логіці Закон виключеного третього: із двох суперечних суджень одне неодмінно є істинним, друге – хибним, а третього і бути не може. Схема закону: Закон достатньої підстави: достовірною треба вважати тільки ту думку, істинність якої достатньо обґрунтована. Закон подвійного заперечення: заперечення заперечення дає твердження, із твердження випливає його подвійне заперечення, а подвійне заперечення рівносильне твердженню. Схема закону: Закон ідемпотентності (з лат. – зберігаючи той самий ступінь): повторення будь-якого висловлення через „і” (кон’юнкція) чи „або” (диз’юнкція) рівнозначне самому висловленню. Схема закону для кон’юнкції: (А٨А) ↔ А („А і А тоді і тільки тоді, коли А”). Схема закону для диз’юнкції: (А٧А) ↔ А („А або А тоді і тільки тоді, коли А”). Закон комутативності (з лат. – зміна): дозволено міняти місцями висловлювання, зв’язані логічними сполучниками „і” (конюнкція) та „або” (диз’юнкція). Схема закону для кон’юнкції: (А٨А) ↔ (А٧А) („А і В тоді і тільки тоді, коли В і А”). Схема закону для диз’юнкції: (А٧В) ↔ (В٧А) („А або В тоді і тільки тоді, коли В або А”). Закон асоціативності (з лат. - з’єднує): дозволено по-різному поєднувати вимолювання, з’єднані з допомогою логічних сполучників „і” (кон’юнкція), „або”(диз’юнкція) тощо. Схема закону для кон’юнкції: ((А٨В)٨С) ↔ (А٨ (В٨С)) („(А і В) і С тоді, і тільки тоді, коли А і (В і С)”). Схема закону для диз’юнкції: (А٧В)٧С) ↔ (А٧(В٧С)) („(А або В) або С тоді і тільки тоді, коли А або (В або С)”). Закон дистрибутивності: (з лат. – розділяю, розподіляю): дозволено розподіляти один логічний сполучник стосовно іншого. Схема закону для кон’юнкції: (А٨(В٧С) ↔ ((А٨В)٧(А٨С) („А і (В або С), якщо і тільки якщо (А і В) або (А і С)”). Схема закону для диз’юнкції: (А٧(В٨С) ↔ ((А٧В)٨(А٧С)) („А або (В і С), якщо і тільки якщо (А або В) і (А або С)”). Закон де Моргана – логічні закони, які пов’язують заперечення, кон’юнкцію і диз’юнкцію. Перший закон де Моргана: заперечення кон’юнкції, еквівалентне диз’юнкції заперечень. Схема закону де Моргана: Другий закон де Моргана: заперечення диз’юнкції еквівалентне кон’юнкції заперечень. Схема закону: Закони контра позиції (з лат. - протиставлення): Перший закон простої контра позиції: якщо з першого висловлення впливає друге висловлювання, то із заперечення другого висловлювання випливає заперечення першого висловлювання. Схема закону: (А→В) → Другий закон простої контра позиції: якщо із заперечення першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає перше висловлювання. Схема закону: Третій закон простої контра позиції: якщо з першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає заперечення першого висловлювання. Схема закону: Четвертий закон простої контра позиції: якщо із заперечення першого висловлювання випливає друге висловлювання, то із заперечення другого висловлювання випливає перше висловлювання. Схема закону:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.149 (0.009 с.) |

 („Хибно, що А і не-А одночасно істинні”).
(„Хибно, що А і не-А одночасно істинні”). („або А, або не-А”).
(„або А, або не-А”).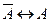 („Хибно, що не-А тоді, тільки тоді коли А ”).
(„Хибно, що не-А тоді, тільки тоді коли А ”). ↔
↔  („Хибно, що А і В тоді і тільки тоді, коли хибно, що А, або хибно, що В”).
(„Хибно, що А і В тоді і тільки тоді, коли хибно, що А, або хибно, що В”). ↔
↔  („Хибно, що А або В і тільки тоді, коли хибно, що А і хибно, що В”).
(„Хибно, що А або В і тільки тоді, коли хибно, що А і хибно, що В”). (”Коли відомо, що якщо А, то В, то якщо не-В, то не-А”).
(”Коли відомо, що якщо А, то В, то якщо не-В, то не-А”). → (В→А). („Коли відомо, що якщо не-А, то не-В, то якщо В, то А”).
→ (В→А). („Коли відомо, що якщо не-А, то не-В, то якщо В, то А”).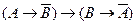 („Коли відомо, що якщо А, то не-В, то якщо В, то не-А”).
(„Коли відомо, що якщо А, то не-В, то якщо В, то не-А”). („Коли відомо, що якщо не-А, то В, то якщо не-В, то А”).
(„Коли відомо, що якщо не-А, то В, то якщо не-В, то А”).


