
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разностью отношений r и s называется множество кортежей, принадлежащих r, но не принадлежащих S. Для этой операции также требуется одинаковая арность отношений.Содержание книги
Поиск на нашем сайте
r – s
Заметим, что с помощью операции разности может быть реализовано удаление кортежа из имеющегося отношения. В этом случае r – исходное отношение, s – отношение, содержащее один удаляемый кортеж.
Декартово произведение r ´ s Пусть r и s – отношения арности k1 и k2 соответственно. Декартовым произведением r´s называется множество кортежей длины k1+k2, первые k1 компонентов которых образуют кортежи, принадлежащие r, а последние k2 – кортежи, принадлежащие s. r ´ s
Проекция Проекция Другими словами, это операция построения «вертикального» подмножества, получаемого путем выбора определенных атрибутов и исключения остальных. Повторяющиеся кортежи исключаются.
Выбор (селекция) sF (r) Пусть F – формула, образованная: операндами, являющимися константами или именами атрибутов, арифметическими операторами сравнения, логическими операторами (и, или, не), тогда выбором (селекцией) sF называется множество кортежей, компоненты которого удовлетворяют условию, заданному формулой F.
Здесь F:(1)=(3) – содержимое первого столбца равно содержимому третьего столбца. Приведем ряд примеров представления запросов с помощью формальных операций для реляционной модели (СТУДЕНТ, ФАКУЛЬТЕТ, СПЕЦИАЛЬНОСТЬ), рассмотренной выше.
Пример 1. Сформировать список студентов (фамилия). Рассмотрим схему отношения СТУДЕНТ. Атрибут «Фамилия» обозначен здесь А 1 Для ответа на запрос необходимо взять проекцию отношения r 1 на столбец А 1. .
Пример 2. Выдать список фамилий и дат рождений студентов, которым на текущую дату (tek_date) больше 35 лет. Рассмотрим то же отношение r 1. Сначала выбираем студентов, которым больше 35 лет:
Затем берем проекцию полученного отношения на столбцы
. Заметим, что можно было бы выполнить эти две операции в другой последовательности – сначала проекция, а затем селекция. Предлагается оценить, какой из этих вариантов лучше по оценке числа выполняемых элементарных действий и объему требуемой памяти.
Пример 3. Выдать список фамилий студентов, обучающихся по специальности «Информационные технологии». Название специальности является атрибутом отношения r 3. Если бы в этом отношении присутствовал атрибут «фамилия», то задача решалась бы аналогично примеру 2. В отношении r 3 присутствует атрибут «код студента», а «фамилия» присутствует в отношении r 1. Для ответа на этот запрос необходимо связывать по «код студента»отношение r 3и отношение r 1. Сначала выберем из отношения r 3кортежи с названием специальности «Информационные технологии». Обозначим полученное отношение rp 1. (Дальнейшие промежуточные отношения будем обозначать последовательно rp 1, rp 2, rp 3и т.д.).
Далее нас будет интересовать только атрибуты A 1 – «код студента» . Поэтому возьмем проекцию на эти столбцы.
Далее необходимо связать отношения отношения r 1 и rp 2(склеить таблицы). Для склейки таблиц используется операция «декартово произведение»:
В отношении Rr 3 присутствуют два одинаковых столбца: A 1 из отношенийя r 1 и A 1 из отношения rp 2. Выбирая из отношения rp 3строки, в которых значения в соответствующих столбцах совпадают, получим сведения о студентов, обучающихся по специальности «Информационные технологии»
R 4 = sentrant. entrant_id = R2. entrant_id (R 3), где A 1 × r 1 и A 1 × rp 2 обозначают соответственно столбец A 1 соответствующей первой и второй составной части декартова произведения. Теперь осталось только выбрать фамилии соответствующих студентов
Получаем требуемый результат. Заметим, что для экономии действий и памяти, перед тем как склеивать таблицы, целесообразно было сделать операцию проекции отношения отношения r 1 на столбцы столбцы A 1, A 2. (чтобы не включать в декартово произведение лишние столбцы).
Введенные пять основных операций реляционной алгебры позволяют реализовать любой запрос к реляционной базе данных. Однако наряду с основными операциями достаточно часто удобно использовать так называемые дополнительные операции реляционной алгебры (которые могут быть выражены через основные).
Пересечение r Ç s Пересечением отношений r и s называется множество кортежей, принадлежащих как r, так и s. Пересечение может быть выражено через операции разности
r Ç s = r – (r – s).
q -соединение q-соединение r и s по столбцам Ai и Aj представляет собой множество таких кортежей в декартовом произведении r и s, что i-й компонент r находится в отношении q c j-м компонентом s, где q – арифметический оператор сравнения. Если q является оператором равенства, то эта операция называется эквисоединением
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.168 (0.009 с.) |




 .
. .
. .
.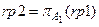 .
. .
. ,
, .
.
 ,
,


