
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скольжение во фрикционной передачеСодержание книги Поиск на нашем сайте 2 вида скольжения Упругое скольженик, геометрическое скольжение. Упругое скольжение возникает из-за упругих деформаций в зоне контакта роликов, зависит от упругих свойств материала из каторыхизгатовлены ролики и велечины крутящих моментов. V1 скорость ведущего ролика V2 скорость ведомого ролика Вариатр позволяет изменять передаточное число. Основы расчета прочности фрикционных передач. Критерии работоспособности Контактные напряжения передач с контактом по линии определяют по формуле Герца
где Q — сила прижатия катков;
К — коэффициент запаса сцепления (коэффициент нагрузки), К= 1,25...2;
Для передач от одного вала к другому вращающего момента необходимо за счёт силы трения приложить к ведомому катку окружную силу
где k – коэффициент запаса сцепления (k = 1,3…1,4); Из вышеприведённой формулы определим силу притяжения катков:Q = kF1/f = 2kT1/(fD1) (2.2.4) Из этой формулы видно, что сила притяжения больше окружной силы в k/f раз, что при k = 1,4, f = 0,04 даёт k/f = 1,4/0,04 = 35 раз. Большие силы притяжения катков создают значительные радиальные нагрузки на опоры валов и вызывают появление больших контактных напряжений на рабочих поверхностях катков, что делает силовые фрикционные передачи громоздкими, а их нагрузочную способность сравнительно невысокой. Для уменьшения в несколько раз силы притяжения применяют катки с клинчатым ободом, трение в которых аналогично трению в клинчатом ползуне, рассмотренному в теоретической механике. Однако в таких катках возникает значительное геометрическое скольжение, существенно уменьшающее срок их службы. Коэффициент полезного действия фрикционных передач в основном определяется потерями в опорах валов. Экспериментально установлено, что для закрытых передач Ременные передачи Ременные передачи – относятся к передачам фрикционного типа. Состоит из двух шкивов охваченных бесконечным ремнём. Достоинство передачи: 1) Возможность передачи вращения между валами, на значительном расстоянии. 2) 3) Недостатки: 1) Большие геометрические размеры 2) Непостоянство передаточного отношения 3) Значительные нагрузки на валы. Типы: 1) В зависимости от сечения ремня различают: · Плоскоременные передачи · Клиновидный ремень (Тяговая способность при прочих равных условиях прим. в 3 раза выше чем у плоскоременной)
· Поликлиновая передача Все преимущества плоско клиноременной ·
Кинематические и геометрические параметры ременных передач
Известные: d1, d2, U, n1, n2 Определяемые: β- угол между ветвями, α- угол обхвата на меньшем шкиве; а- межосевое расстояние; l- длина ремня.
Силы и силовые зависимости в ременной передаче
Т=0Т>0
λ+∆
F0 F1 1) Передача стоит: F0- Усилие от предварительного натяжения ремня 2) Передача работает: 3) F1- Усилие ведущей ветви ремня F2- Усилие ведомой оси ремня
Получим систему из двух уравнений с тремя неизвестными.
α duφ
F+dfF
1)Из условия равновесия элемен. сектора dφ получим следующее ур-ие
Спроецируем все силы на вертикальную ось
Исключив dR получим Получим дополнительноеур-ие, которое связывает силы F и угол обхвата α Используем систему двух ур-ийи учитывая уравнение efα получим:
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (2.2.5),
(2.2.5), ;
; — приведенный радиус кривизны:
— приведенный радиус кривизны:  ,
, 
 — приведенный модуль упругости,
— приведенный модуль упругости, - коэффициент Пуассона
- коэффициент Пуассона (2.2.2),
(2.2.2), (2.2.3),
(2.2.3), , для открытых передач -
, для открытых передач -  .
. Плавность и бесшумность в работе
Плавность и бесшумность в работе Возможность предохранения от перегрузок
Возможность предохранения от перегрузок

 Зубчатоременная Работает по принципу зацепления. Может использоваться в точных кинематических цепях. Обладает высокой тяговой способностью.
Зубчатоременная Работает по принципу зацепления. Может использоваться в точных кинематических цепях. Обладает высокой тяговой способностью. ;
;  ;
; 




 F0F2
F0F2 – окружная сила, полезной
– окружная сила, полезной −F2
−F2 F2=2F0
F2=2F0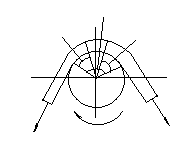 Данная задача была решена Эйлером.
Данная задача была решена Эйлером.



 . Проинтегрируем обе части.
. Проинтегрируем обе части. ;
; 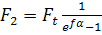 ;
; 



