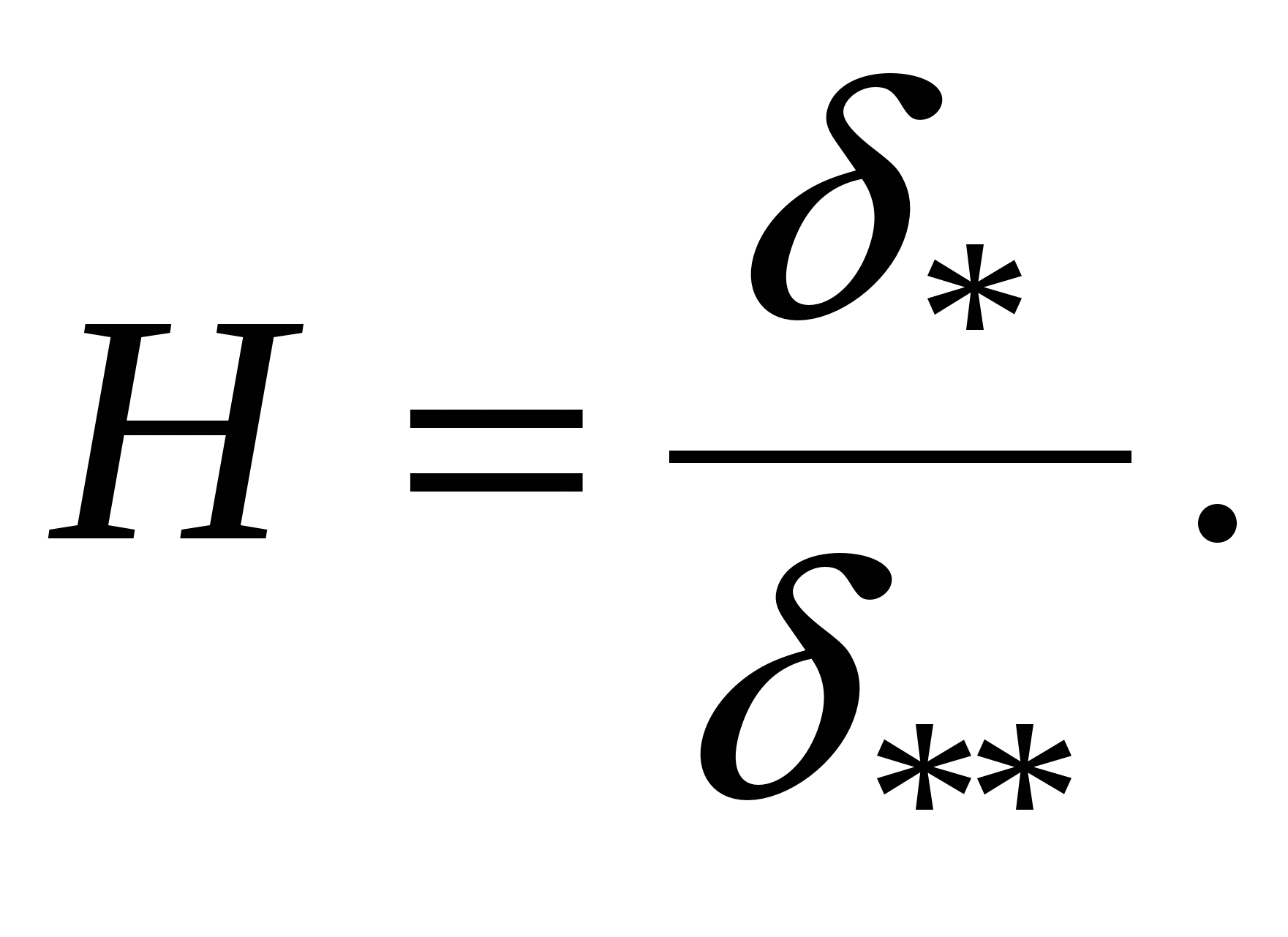Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потери в подводах, отводах и проточной части насосовСодержание книги
Поиск на нашем сайте
Гидравлические потери – наиболее сложные с точки зрения их теоретического и экспериментального исследования. Основная причина этого в сложности физических процессов, происходящих в центробежных насосах. Чтобы более точно оценить гидравлические потери, необходимо иметь правильное представление о физике явлений, возникающих при течении вязкой жидкости. Движение вязкой жидкости в общем случае сопровождается рассеиванием энергии, т.е. гидравлическими потерями. Причиной возникновения этих потерь является сопротивление вязкой жидкости изменению формы. При больших числах Рейнольдса, характерных движению в турбомашинах, вязкие возмущения ограничены пограничным слоем и гидродинамическим следом за телом, где и сосредотачиваются гидродинамические потери. Поэтому для анализа гидравлических потерь необходимо остановиться на анализе физических явлений у стенок, т.е. в пограничном слое. Дифференциальные уравнения стационарного движения в пограничном слое были получены Прандтлем путем упрощения уравнений Навье-Стокса
Причем Профиль пограничного слоя зависит от ряда факторов, прежде всего от характера течения (конфузорного или диффузорного), от числа Рейнольдса, степени турбулентности потока. Большое влияние на характер пограничного слоя оказывает закон изменения статического давления вдоль обтекаемой поверхности Математическая точка отрыва внешнего потока от контура обтекаемого тела характеризуется условием
Точные решения дифференциальных уравнений турбулентного пограничного слоя до настоящего времени не разработаны, и для его исследования применяются приближенные методы. Для получения приближенных способов необходимо отказаться от требования удовлетворения дифференциальных уравнений пограничного слоя для каждой частицы, а ограничиться выполнением граничных условий и контурных связей на стенке и при переходе к внешнему течению, а также выполнением только суммарного соотношения, получаемого из дифференциальных уравнений пограничного слоя как некоторое среднее по толщине слоя. Такое среднее дает уравнение импульсов или интегральное соотношение Кармана для плоского несжимаемого пограничного слоя:
где
U - скорость внешнего потока; Vy - скорость в пограничном слое или где
|
|||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 8; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.152.151 (0.007 с.) |

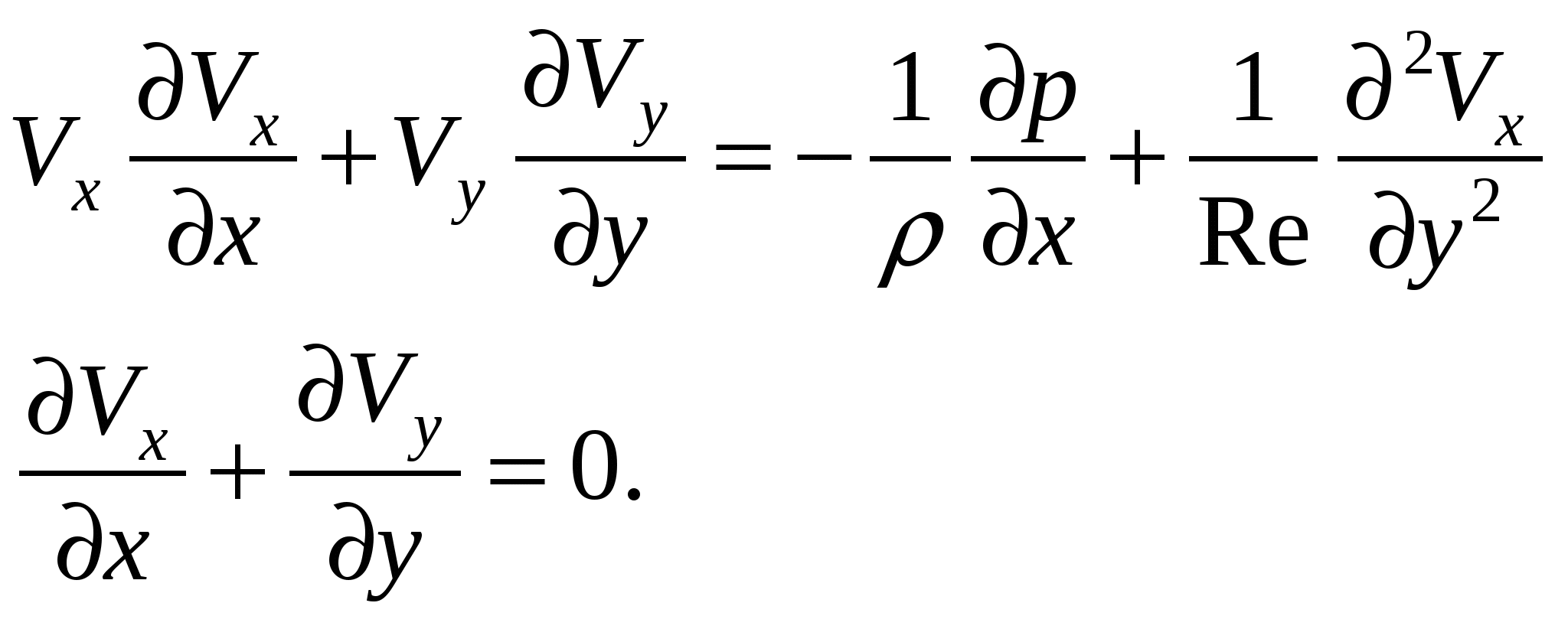 (2.151)
(2.151)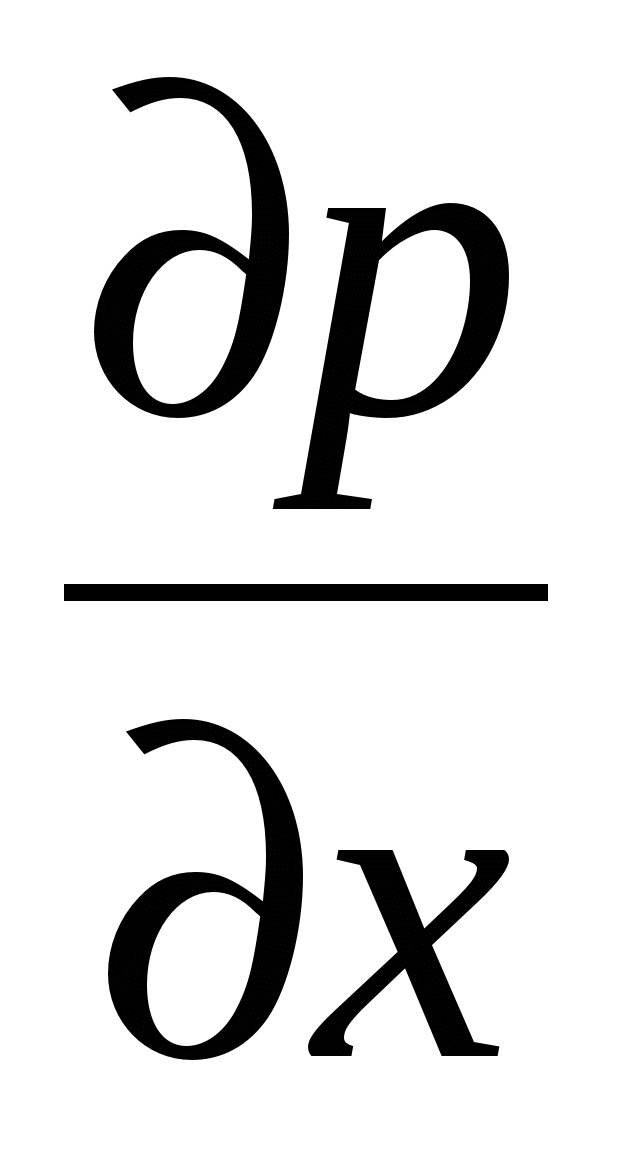 является граничным условием, заданным внешним потоком, т.е. давление р уже не является неизвестной величиной.
является граничным условием, заданным внешним потоком, т.е. давление р уже не является неизвестной величиной.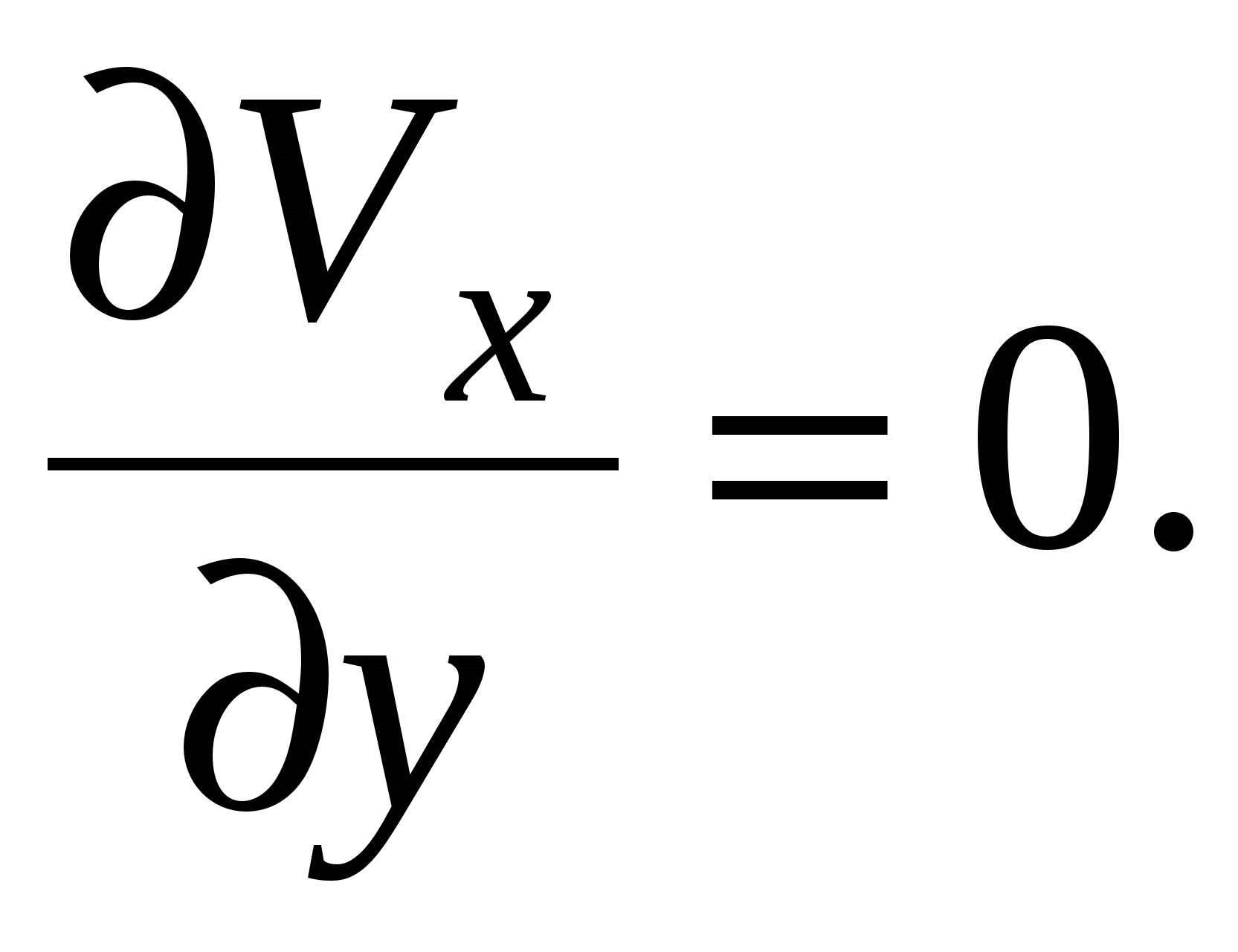 Преобразуя дифференциальные уравнения пограничного слоя так, чтобы масштабом для координат являлась относительная толщина пограничного слоя d1, можно исключить из них Re. Это указывает на то, что точка отрыва пограничного слоя не зависит от Re ,и, следовательно, потери вихреобразования также не зависят от числа Re.
Преобразуя дифференциальные уравнения пограничного слоя так, чтобы масштабом для координат являлась относительная толщина пограничного слоя d1, можно исключить из них Re. Это указывает на то, что точка отрыва пограничного слоя не зависит от Re ,и, следовательно, потери вихреобразования также не зависят от числа Re.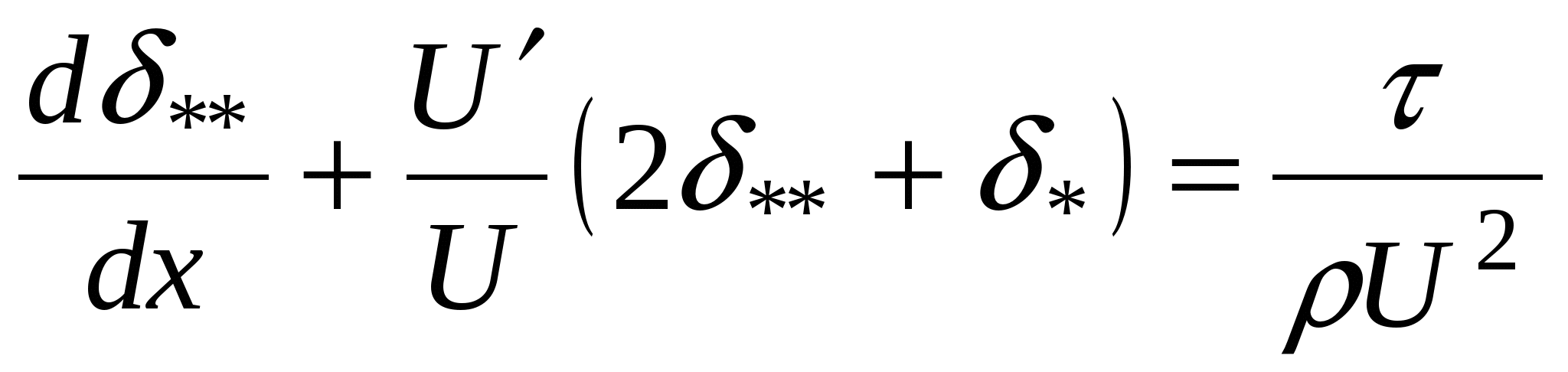 , (2.152)
, (2.152)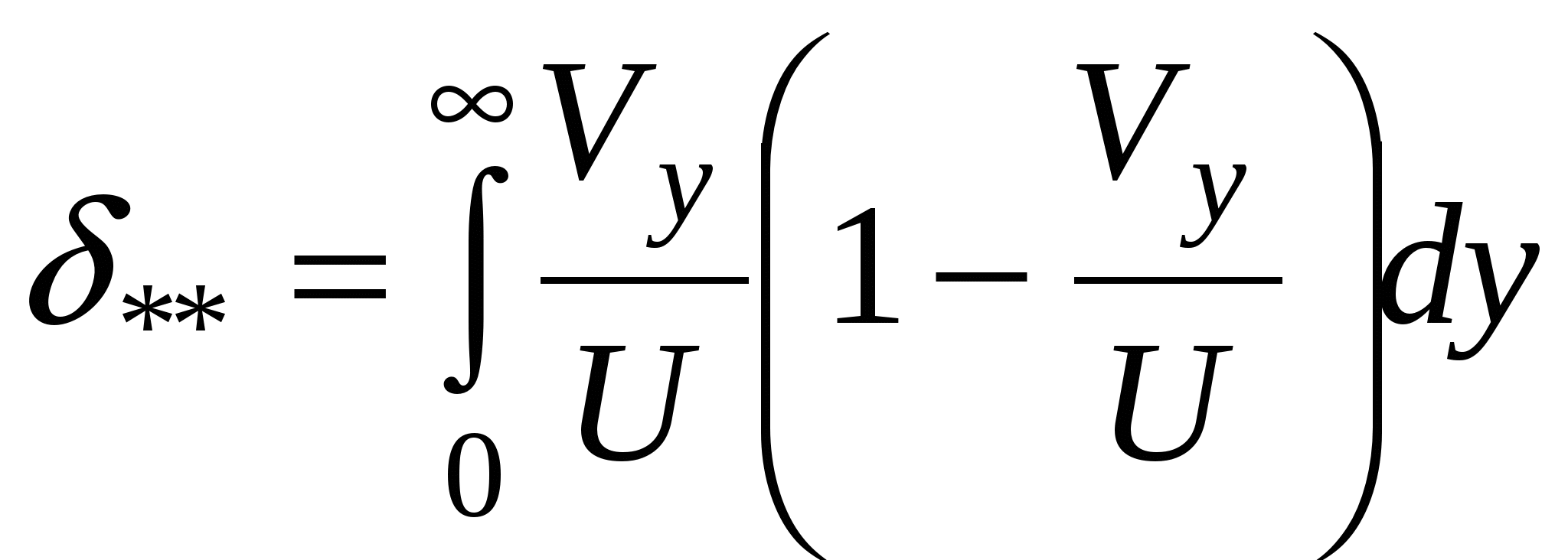 - толщина потери импульса;
- толщина потери импульса;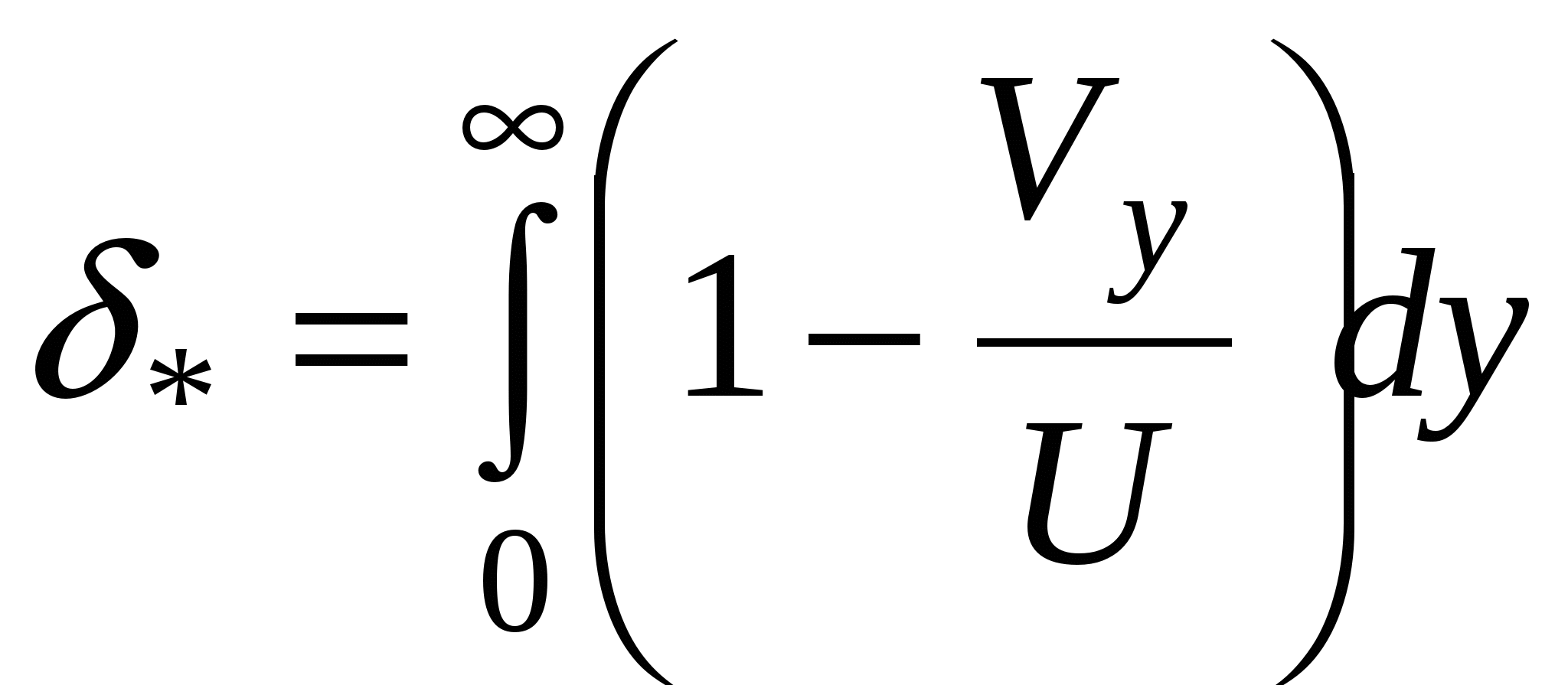 - толщина вытеснения;
- толщина вытеснения;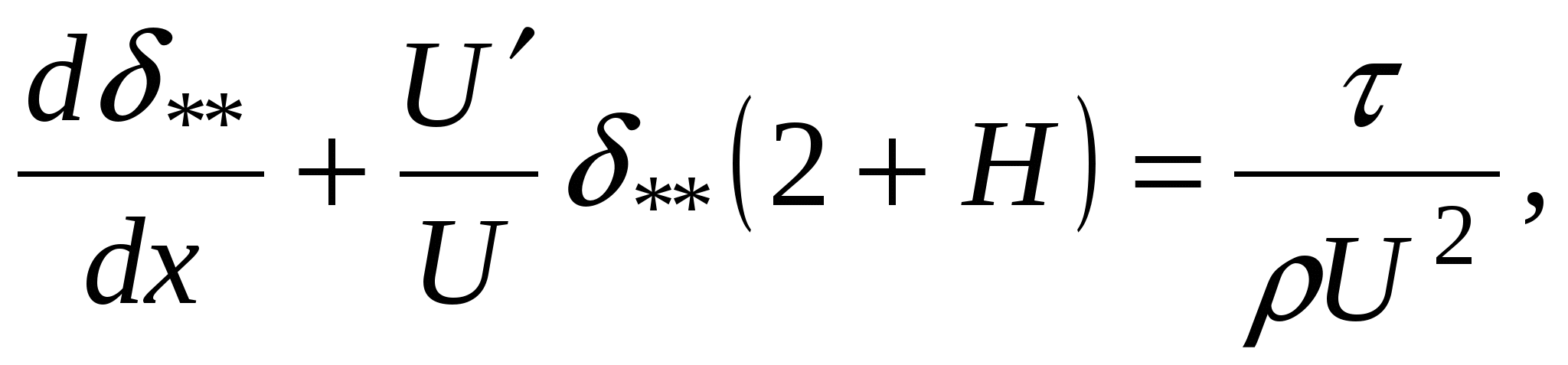 (2.153)
(2.153)