
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стереографічна проекція кристалів.Содержание книги
Поиск на нашем сайте
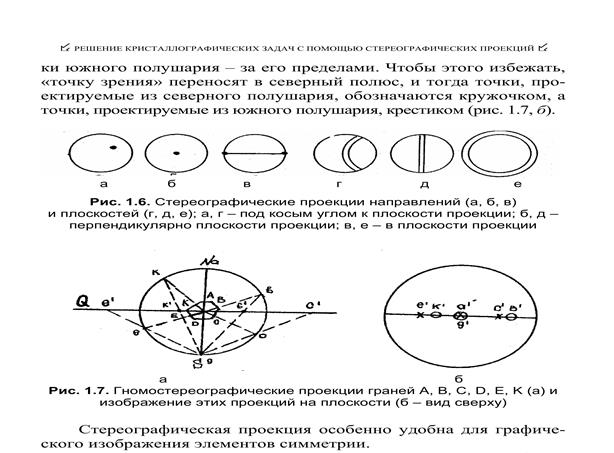
11. Стереографічна проекція кристалів.
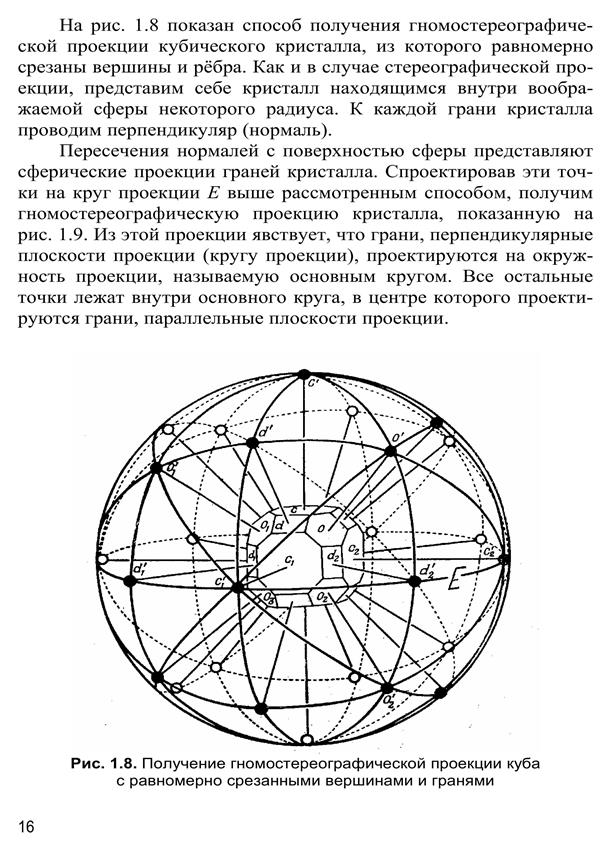
12. Гномостереографічна проекція кристалів.
13. Індекси вузлів атомів, індекси напрямів у кристалі, індекси площин кристалів. Кристаллографические индексы узлов, плоскостей и направлений
Прямые и плоскости, проходящие через узлы пространственной решетки, называют соответственно узловыми прямыми и плоскостями. Все узловые прямые или плоскости, одинаково ориентированные в пространстве, составляют семейство прямых или плоскостей. Они кристаллографически идентичны и обладают одинаковыми периодами идентичности или соответственно межплоскостным расстоянием. Индексы узлов. Положение любого узла решетки относительно выбранного начала координат определяется заданием 3-х координат: x, y, z. Эти координаты можно выразить так: где a, b, c - параметры решетки; m, n, p - целые числа. Если за единицы измерения длин принять параметры решетки, то координатами узла будут просто числа m, n, p. Эти числа называются индексами узла и записываются следующим образом: [[mnp]]. В сложных решетках для всех узлов, не лежащих в вершинах элементарных ячеек, числа m, n, p будут дробными. Например, узел, находящийся в центре объема ячейки и ближайший к началу координат, имеет символ [[1/2 1/2 1/2]] Индексы плоскостей. Положение плоскости определяется заданием трех отрезков A, B, C, которые она отсекает на осях решетки. Индексы такой плоскости отыскиваются следующим образом. Выражают отрезки A, B, C в осевых единицах и записывают величины, обратные этим отрезкам: 1/A, 1/B, 1/C. Полученные дроби приводят к общему знаменателю. Пусть таковым будет число D. Целые числа и являются индексами плоскости. Они записываются так: (hkl). Для плоскостей, параллельных какой-либо координатной оси, соответствующий индекс равен нулю (отсекаемый отрезок равен ¥). В случае, если плоскость пересекает кристаллографическую ось в отрицательном направлении, над соответствующим индексом следует ставить знак «минус», например, Плоскости, отсекающие на каждой по равному числу осевых единиц обозначают символом (111). В кубической решетке их называют плоскостями октаэдра, так как система подобных плоскостей, равноотстоящих от начала координат, образует октаэдр.
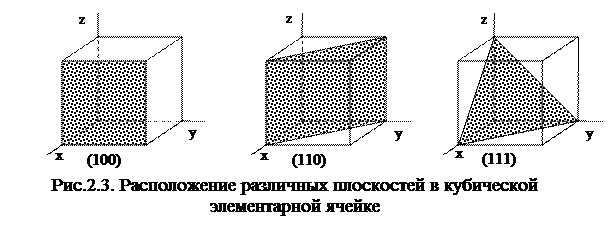
Плоскости, отсекающие на двух осях по равному числу осевых единиц и параллельные третьей оси (например оси z), обозначают (110). В кубической сингонии их называют плоскостями ромбического додекаэдра, так как система подобных плоскостей образует двенадцатигранник, каждая грань которого - ромб. Плоскости, пересекающие одну ось и параллельные двум другим (например, осям y и z), обозначают (100) и называют в кубической решетке плоскостями куба, так как система подобных плоскостей образует куб. Основные индексы Миллера для кубической решетки приведены на рис.2.3.
Для обозначения плоскостей гексагональных кристаллов пользуются 4осной системой координат: три оси (а1, а2, а3), расположенные под углом 120° друг к другу, лежат в плоскости базиса, четвертая ось (c) перпендикулярна ей. Каждая плоскость обозначается 4 индексами (hkil). Дополнительный индекс i ставится на третьем месте и вычисляется через индексы h и k:
Индексы направлений. Под кристаллографическими индексами направления понимают три целых взаимно простых числа, пропорциональных координатам любого атома, расположенного на данном наплавлении, измеренным в осевых единицах. При установлении кристаллографических индексов данного направления его необходимо перенести параллельно самому себе в начало координат. Кристаллографические индексы направлений заключают в квадратные скобки и обозначают буквенно [uvw]. Индексы важнейших направлений в кубической решетке приведены на рис.2.4. Для кубической сингонии индексы направления [uvw], перпендикулярного к плоскостям (hk1), числено равны индексам этой плоскости. Так, индексы по оси x равны [100], а индексы плоскости, перпендикулярной оси x, равны (100).
Индексы направления, связывающего две частицы в решетке, равны разности координат этих узлов, приведенных к целому виду. Индексы направления [uvw], по которому пересекаются две плоскости, связаны с индексами этих плоскостей (h1k1l1) и (h2k2l2) следующей системой уравнений:
Аналогично индексы плоскости (hkl), в которой лежат два направления [u1v1w1] и [u2v2w2], определяются из симметричной системы:
|
||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.196.68 (0.009 с.) |







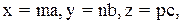 (2.2)
(2.2)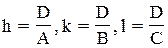 (2.3)
(2.3)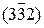 .
.
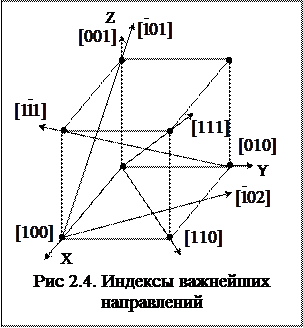
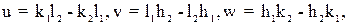 (2.4)
(2.4)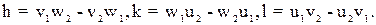 (2.5)
(2.5)


