
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Просторові групи симетрії кристалічної решітки. Порядок запису символів просторової групи. Приклади.Содержание книги
Поиск на нашем сайте
Просторова група симетрії – сукупність усіх можливих елементів симетрії кристалічної структури, так само характеризує симетрії кристалічної структури, як точкова група симетрії характеризує симетрію зовнішньої форми кристала та його фізичні властивості. Просторова група характеризується числом симетрично еквівалентних позицій (точок). Вибравши точку в середині елементарної комірки і розмноживши її усіма елементами просторової групи одержимо правильну систему точок, яка (буває загальною, окремою (індивідуальною)). Загальна правильна система точок, не лежить на елементах симетрії, а окремо (індивідуально) знаходиться на елементах симетрії.
Кратністю правильної системи точок – називається число точок в елементарній комірці, симетрично еквівалентних одна одній. Кратність загальної правильної системи точок аналогічна числу граней простої форми. Кратність вища, ніж для окремої (індивідуальної) в правильній системі точок.
Приклади запису просторових груп структура Просторова група Кристалографічний клас (точкова група) Короткий символ Повний символ Cu,NaCl Fm3m F m3m W, Im3m I m3m C (алмаз) Fd3m F m3m Mg,графіт P63/mmc P63/m2/m2/c 6/mmm
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 4; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.128.229 (0.009 с.) |

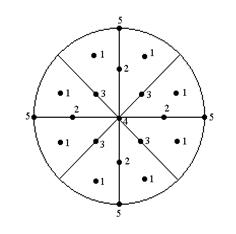 Загальна правильна система точок має три ступені свободи ( не пов’язана з елементами симетрії ).
Загальна правильна система точок має три ступені свободи ( не пов’язана з елементами симетрії ).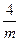 3
3 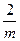
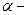 Fe
Fe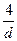 3
3 


