
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання до лабораторної роботиСодержание книги
Поиск на нашем сайте
Теоретичні відомості
Проектування великих багатокомпонентних систем пов’язано з плануванням одночасного виконання кількох робіт, іншими словами, зі структурним плануванням. Побудова мережевої моделі починається з розбиття проекту на чітко визначені роботи, для кожної з яких визначається тривалість. Робота – це деякий процес, який призводить до досягнення визначеного результату, вимагає витрат ресурсів і має тривалість у часі. За кількістю витраченого часу робота може бути дійсною, тобто такою, що вимагає витрат часу, або фіктивною, що формально витрат часу не потребує. Фіктивна робота може існувати насправді, наприклад „передача документів від одного відділу до іншого”. Якщо тривалість такої роботи достатньо мала у порівнянні з тривалостями інших робіт проекту, то формально її приймають рівною нулю. Існують також фіктивні роботи, яким у реальності не відповідають ніякі дії. Такі фіктивні роботи тільки показують зв′язок між іншими роботами мережевої моделі. Роботи пов′язані одна з іншою так, щоб виконання одних робіт можна було почати тільки після завершення деяких інших. Назвемо подією момент часу, коли завершається одна робота і починаються інші. Подія не має протяжності у часі. Взаємозв′язок робіт і подій, нобхідних для досягнення кінцевої мети проекту, зображується за допомогою мережевого графіку (мережевої моделі). Роботи зображуються стрілками, які поєднують варшини, що зображують події. Початок і закінчення будь-якої роботи описують парою подій, перша з яких – початкова, друга кінцева. Тому для зазначення конкретної роботи використовують код роботи, що складається з номерів початкової (i-ї) та кінцевої (j-ї) подій (рис. 1).
Рис. 1.1 - Кодування роботи.
Будь-яка подія може вважатись виконаною тільки тоді, коли закінчаться усі роботи, що в неї входять. Тому роботи, які починаються з деякої події, не можуть початися, поки не будуть завершені усі роботи, що входять у цю подію. Подія, яка не має попередніх подій, тобто, з якої починається проект, називається початковою (вихідною).Вона позначається І. Подія, яка не має наступних подій і відображає кінцеву мету проекту, називається завершальною. Вона позначається С. При побудові мережевого графіку необхідно виконувати такі правила: - довжина стрілки на графіку не залежить від тривалості виконання роботи - стрілка може не бути прямолінійним відрізком; - для дійсних робіт використовують суцільні стрілки, а для фіктивних пунктирні; - кожна операція може бути представлена тільки однією стрілкою; - не може існувати робіт з однаковими кодами; - стрілки, як правило, не повинні перетинатись; - не повинно бути стрілок, що направлені справа наліво; - номер початкової події повинен бути меншим, ніж номер кінцевої події; - не повинно бути „висячих” подій, крім початкової; - не повинно бути тупикових подій, крім завершальної; - не повинно бути циклів (рис.2).
Рис.1. 2 - цикл
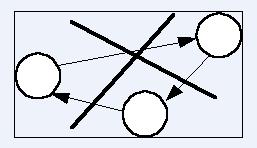
Приклад мережевого графіка наведений на рис. 3. Початкові роботи проекту А, В, С, тому їх зобразили трьома стрілками, що виходять з з початкової події 1. Умова, що А і В передують роботі D, означає, що стрілки робіт А і В повинні закінчитися в одній події з якої вийде стрілка роботи D. Для усунення паралельності робіт, ввели додаткову подію 2, у яку ввійде робота В, після чого можна поєднати події 2 і 3 стрілкою фіктивної роботи. У цьому випадку вона не відповідає ніякій реальній роботі, а відображає логічний зв′язок між роботами В і D. З аналогічною метою запобігти паралельності робіт H і E введена подія 5. Фіктивна робота (4,7) введена у відповідності до вимоги, що С, D, F, J повинні передувати К, при цьому С і F передують G. Усе це призвело до введення події 4 і фіктивної роботи (4,7), яка порушує правило не перетинати інші роботи. Роботи L, I, G є завершальними, тому їх поєднали у подію 9.
Рис. 1.3 - Приклад мережевого графіка
Алгоритм побудови дуг (робіт): Крок 1: Початкова подія має ранг 0. Будуємо усі роботи, що виходять з події 0. Нумеруємо їх. Крок k: Усі події, які не мають вхідних дуг, отримують ранг k. Будуємо усі роботи, що виходять з події k. Нумеруємо ці роботи послідовними числами натурального ряду, починаючи з найменшого не використаного у попередньому кроці алгоритму. Критичний шлях на графіку – це шлях максимальної довжини від початку до завершення. Обчислення термінів подій і робіт. Найбільш ранній з можливих термінів
Найбільш пізній з можливих термінів
Найбільш ранній термін початку роботи (i,j)
Найбільш ранній термін закінчення роботи (i,j)
Найбільш пізній термін початку роботи (i,j)
Найбільш пізній термін закінчення роботи (i,j)
Резерв часу
Шлях, який поєднує події з нульовим резервом часу, називається критичним шляхом. Повний резерв часу роботи
Вільний резерв часу роботи
Усі розрахунки зручно звести до таблиці (див. Приклад виконання роботи)
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 3; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.77.51 (0.005 с.) |


 ;
;
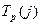 здійснення події j – це термін, необхідний для виконання усіх робіт, що передують даній події, тобто довжина максимального шляху із усіх шляхів, що передують події j.
здійснення події j – це термін, необхідний для виконання усіх робіт, що передують даній події, тобто довжина максимального шляху із усіх шляхів, що передують події j.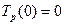 ,
,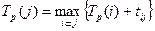 (1.1)
(1.1)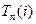 здійснення події i – це термін, перевищення якого викликає аналогічну затримку настання завершальної події.
здійснення події i – це термін, перевищення якого викликає аналогічну затримку настання завершальної події.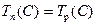 ,
,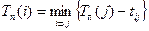 , (1.2)
, (1.2)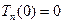 .
.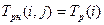 (1.3)
(1.3)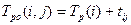 (1.4)
(1.4)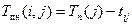 (1.5)
(1.5)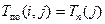 (1.7)
(1.7)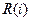 події
події 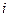 - це проміжок часу, на який може бути відсрочено виконання цієї події.
- це проміжок часу, на який може бути відсрочено виконання цієї події.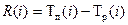 . (1.8)
. (1.8)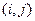 – це максимальна кількість часу, на яку можна збільшити тривалість роботи
– це максимальна кількість часу, на яку можна збільшити тривалість роботи 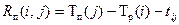 . (1.10)
. (1.10)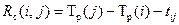 (1.11)
(1.11)


