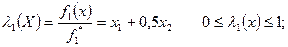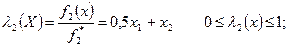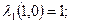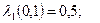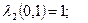Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Питання для контролю та самостійної роботиСодержание книги
Поиск на нашем сайте
Зміст звіту 1. Тема роботи, завдання. 2. Роздруківка усіх потрібних проміжних таблиць і графіків. 3. Аналіз отриманих результатів. 4. Висновки з роботи.
Питання для контролю та самостійної роботи
1. Основні переваги систем на основі нечіткої логіки. 2. Механізм логічного висновку у системі на основі нечіткої логіки. 3. Побудова результуючої функції приналежності. 4. Основні відомості про пакет Matlab і його частини Fuzzy Logic Toolbox.
Лабораторна робота 4. Багатокритеріальна векторна оптимізація.
Мета роботи: Познайомитись з особливостями багатокритеріальних задач на прикладі задач лінійного програмування. Навчитися знаходити оптимальне за Парето значення розв′язку багатокритеріальної задачі.
Теоретичні відомості
Векторні багатокритеріальні задачі виникають при проектуванні технічних систем, при розв′язанні економічних задач та в інших галузях. Нехай
Функціонування технічної системи направлено на виконання визначених цілей-критеріїв, функціонально пов′язаних з вектором змінних Вважаємо, що кожна компонента векторного критерія намагається максимізувати своє значення в області обмежень (4.1). У загальному вигляді, точки оптимуму, отримані при розв′язанні задачі окремо за кожним критерієм, не співпадають, тому з точки зору математичного програмування ця задача є некорректною, тобто, якщо один з критеріїв досяг свого оптимуму, то покращення за іншими компонентами векторного критерія неможливо. В. Парето запропонував метод пошуку множини точок, які неможливо покращити, тобто таких точок, що покращення одного з критеріїв призведе до погіршення інших. Така множина точок, оптимальних за Парето, лежить між точками оптимуму, отриманих при розв′язанні задачі окремо по кожному критерію. Розглянемо задачу оптимізації.
З математичної точки зору обмеження (4.1) означають деяку область існування (допустима область) фазових змінних. Припустимо, що задача має декілька цілей (цільових функцій)
Знайти ´
При виконанні обмежень (4.1).
З точки зору класичного математичного програмування така задача є некоректною, окремо взятий максимум по окремому критерію не досягається при максимізації інших критеріїв. Тобто, точки максимума, отримані при реалізації кожного критерія окремо, не співпадають між собою. Тому будемо використовувати означення оптимальності по Парето. Головна ідея методу Парето є в тому, що на першому етапі потрібно розв´язати окремо кожну з задач (4.2), тобто знайти такі
............
Іншими словами, потрібно знайти максимуми Абсолютні значення чисел
Назвемо ці параметри відносними оцінками цільових функцій. Ця операція дозволяє усі цільові функції розглядати у одних і тих же відносних величинах На третьому етапі, вважаючи усі критерії рівнозначними, розвязуємо для них мінімаксну задачу теорії ігор:
Розглянемо приклад розв´язання таких задач. Це буде задача лінійного програмування з двома змінними і двома цільовими функціями.
Обмеження:
Крок 1. Окремо розв´язуємо кожну з задач, графічним методом (рис.4.1 і рис.4.2 відповідно).
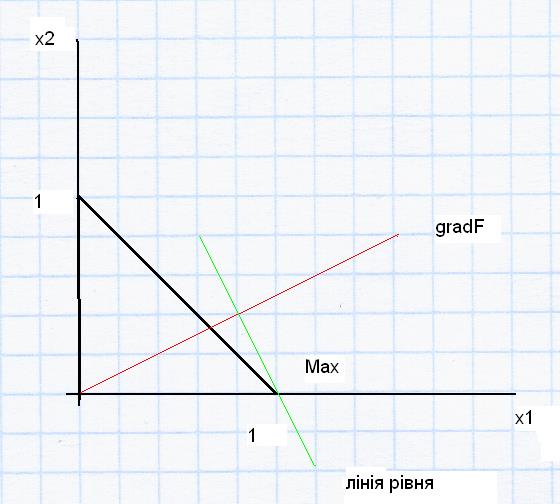
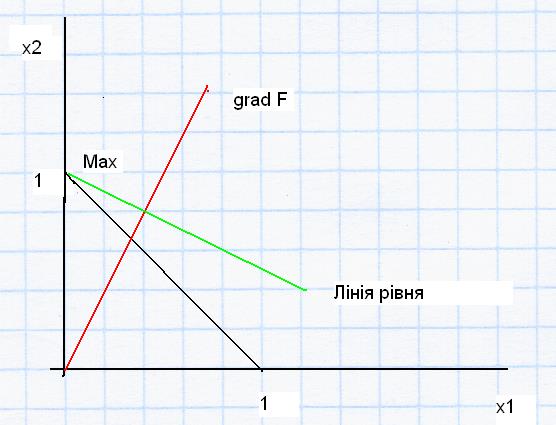
Рис.4.1 Графічне розвязання першої задачі Знайдемо
Рис.4.2 Графічне розвязання другої задачі
Знайдемо Крок 2 Проведемо нормалізацію критеріїв.
(4.7)
Легко бачити, що
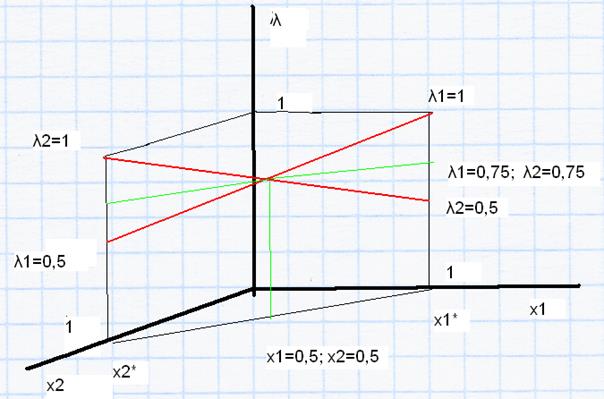
Крок 3. Зробимо графічну побудову, де зобразимо усі можливі значення критеріїв λ1 і λ2.(рис. 4.3). На тому ж рисунку зручно зробити графічне розвязання задачі мінімакса, тобто задачі теорії ігор. Оптимальна точка заходиться на перетині ліній, що поєднують граничні значення критеріїв λ1 і λ2. Це точка х1 = х2 =0,5. У цій точці λ1 = λ2 = 0,75. Це і є розв´язком задачі. Виявляється, що у оптимальному по Парето плані кожна з цільових функцій „наповнилась” на 75%. Рис. 4.3. Графічна побудова до кроку 3
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 3; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.006 с.) |

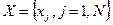 вектор змінних параметрів технічної системи. Звязок між цими змінними встановлюється відповідними співвідношеннями (обмеження моделі):
вектор змінних параметрів технічної системи. Звязок між цими змінними встановлюється відповідними співвідношеннями (обмеження моделі):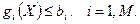 (4.1)
(4.1)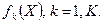 (
( 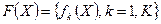 ), який називають векторним критерієм, або векторною цільовою функцією.
), який називають векторним критерієм, або векторною цільовою функцією.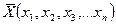 - фазові змінні. Між цими змінними існують певні зв´язки і на ці зв´язки накладені обмеження (4.1):
- фазові змінні. Між цими змінними існують певні зв´язки і на ці зв´язки накладені обмеження (4.1):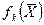 . Тобто потрібно знайти такі значення фазових змінних
. Тобто потрібно знайти такі значення фазових змінних 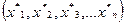 , які б забезпечили розв´язання задачі:
, які б забезпечили розв´язання задачі: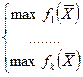 (4.2)
(4.2)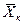 , які б задавольнили відповідно одну з задач:
, які б задавольнили відповідно одну з задач: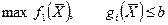
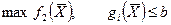 (4.3)
(4.3)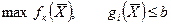
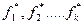 кожної з цільових функцій окремо на обмеженнях (4.1).
кожної з цільових функцій окремо на обмеженнях (4.1).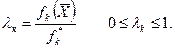 (4.4)
(4.4)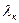 , які фактично показують процент досягнення оптимальної величини цільової функції.
, які фактично показують процент досягнення оптимальної величини цільової функції.
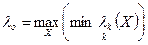 (4.5)
(4.5)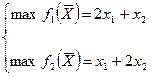 (4.6)
(4.6)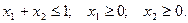
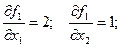 Тоді
Тоді 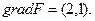 Лінія рівня проходить перпендикулярно градієнту і дотикається останньої точки області у точці максимуму з координатами (1; 0). Цільова функція у цій точці дорівнює
Лінія рівня проходить перпендикулярно градієнту і дотикається останньої точки області у точці максимуму з координатами (1; 0). Цільова функція у цій точці дорівнює 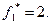
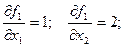 Тоді
Тоді 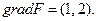 Точка максимуму (0; 1). Цільова функція у цій точці дорівнює також
Точка максимуму (0; 1). Цільова функція у цій точці дорівнює також