
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекурсивные (БИХ) и нерекурсивные (КИХ) фильтрыСодержание книги
Поиск на нашем сайте
Согласно полученному выше разностному уравнению дискретного фильтра очередной выходной отсчет рассчитывается на основе предыдущих выходных отсчетов. Таким образом получается рекурсия и фильтр называется рекурсивным или фильтром с бесконечной импульсной характеристикой (БИХ или в англоязычной литературе IIR infinitе impulse response). Бесконечная импульсная характеристика получается ввиду того, что предыдущее значение на выходе фильтра отлично от нуля, значит, текущее значение также будет отлично от нуля (и оно же будет предыдущим для следующего отсчета на выходе), значит, и следующий отсчет на выходе будет отличен от нуля. Рассмотрим пример. Пусть имеется БИХ-фильтр первого порядка с передаточной функцией:
Очевидно, что
Рассчитаем импульсную характеристику фильтра. Для этого необходимо подать на вход сигнал
Рисунок 4: Импульсная характеристика БИХ фильтра
Видно, что следующий отсчет импульсной характеристики в 2 раза меньше чем предыдущий, и таким образом импульсная характеристика убывает, но никогда не достигает нуля, хотя стремится к нему, т.е. является бесконечной. Если же все коэффициенты am=0 (разумеется, кроме коэффициента a0, который нельзя приравнивать к нулю), то получим фильтр, отсчеты на выходе которого, зависят только от входных отсчетов:
Такой фильтр называется нерекурсивным или фильтром с конечной импульсной характеристикой (КИХ) или как еще говорят FIR (finite impulse response). Отсчеты импульсной характеристики КИХ фильтра полностью совпадают с коэффициентами bm и при k>N импульсная характеристика КИХ фильтра равна нулю. Важно также отметить, что передаточная характеристика КИХ фильтра имеет в знаменателе только a0 и не имеет полюсов. При переходе из комплексной s – плоскости в комплексную z-плоскость все бесконечно-повторяющиеся нули и полюса дискретного фильтра в s плоскости отображаются в конечное количество нулей и полюсов в z-плоскости. Тогда выражение для передаточной характеристики дискретного фильтра может быть представлено при помощи подстановки (7) через конечное количество нулей и полюсов в z-плоскости как:
где
|
|||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.198 (0.008 с.) |

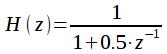 (20)
(20)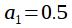
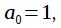 и
и 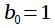 . Разностное уравнение данного фильтра имеет вид:
. Разностное уравнение данного фильтра имеет вид: 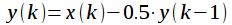 (21)
(21)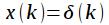 . Графически расчет импульсной характеристики представлен на рисунке 4.
. Графически расчет импульсной характеристики представлен на рисунке 4.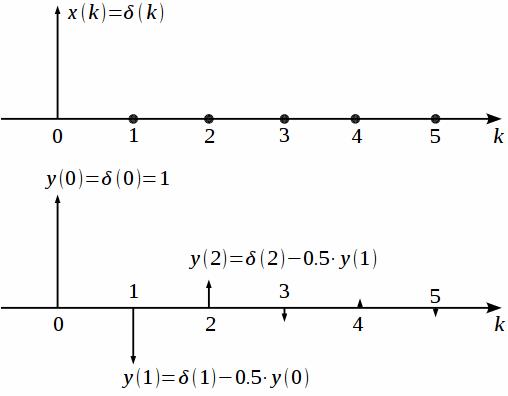
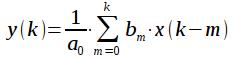 (22)
(22)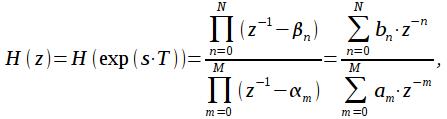
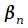 и
и 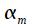 - отображение нулей и полюсов дискретного фильтра в z плоскости, а
- отображение нулей и полюсов дискретного фильтра в z плоскости, а 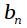 и
и 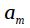 - коэффициенты дискретного фильтра, полученные путем раскрытия произведений нулей и полюсов и приведении подобных слагаемых. Таким образом, главный вывод, который мы должны сделать заключается в следующем: при переходе от аналогового фильтра к дискретному, образ по Лапласу становится периодическим по мнимой оси, а количество нулей и полюсов фильтра бесконечным. Но при переходе в комплексную z – плоскость мы получаем снова конечное количество нулей и полюсов, и соответственно конечное количество коэффициентов дискретного фильтра. Поэтому z-преобразование можно считать аналогом преобразования Лапласа для дискретных фильтров.
- коэффициенты дискретного фильтра, полученные путем раскрытия произведений нулей и полюсов и приведении подобных слагаемых. Таким образом, главный вывод, который мы должны сделать заключается в следующем: при переходе от аналогового фильтра к дискретному, образ по Лапласу становится периодическим по мнимой оси, а количество нулей и полюсов фильтра бесконечным. Но при переходе в комплексную z – плоскость мы получаем снова конечное количество нулей и полюсов, и соответственно конечное количество коэффициентов дискретного фильтра. Поэтому z-преобразование можно считать аналогом преобразования Лапласа для дискретных фильтров.


