
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мэ. Решения. 11 класс. 2015год
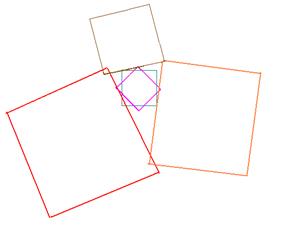
1. По условию откуда следует требуемое утверждение. 2. Пример конфигурации из пяти квадратов, которые попарно пересекаются, но никакие три из них не имеют общей точки, приведён на рисунке.
Ответ: нет. 3. Представим левую часть в виде
Если x не принадлежит интервалу (0, 1), то левая часть заведомо положительна. Сделаем оценку при 0 < x < 1.
В силу неравенства между средним арифметическим и средним геометрическим имеем
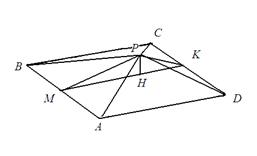
причём равенство достигается только при Равенство возможно лишь при Ответ: ни одного. 4. Среди боковых граней пирамиды есть правильный треугольник. Можно считать, что это треугольник PAB. Пусть PM – его медиана, которая также является и его высотой. Тогда пирамида симметрична относительно плоскости, содержащей PM и перпендикулярной к AB. Рассмотрим возможное расположение боковой грани, которая является прямоугольным треугольником. Она может примыкать к грани PAB, или лежать напротив неё. В первом случае оба треугольника PAD и PBC являются прямоугольными. Прямыми углами в этих треугольниках могут быть только углы PAD и PBC. Высота такой пирамиды совпадает с отрезком PM и равна
Во втором случае прямоугольный треугольник PCD является равнобедренным, и прямой угол – это угол при вершине S. Высота PK такого треугольника является также его медианой и равна 2. Высота пирамиды совпадает с высотой треугольника PMK, опущенной из вершины P.
Находя площадь треугольника PMK по формуле Герона, получаем Ответ: 5. Построим граф G, вершины которого соответствуют городам, а рёбра – дорогам. По условию граф является связным и из любой вершины выходит ровно три ребра. Число рёбер графа G равно 3024. Закрасим вершины G в два цвета следующим образом. Выберем произвольную вершину v0 и закрасим её в белый цвет. Остальные вершины будем закрашивать по следующему правилу. Для произвольной вершины v обозначим d(v) число дорог в маршруте, ведущем из v0 в v и проходящем по наименьшему числу дорог. Вершину v закрасим в белый цвет в том и только том случае, когда число d(v) чётно. В случае, когда d(v) нечётно, вершину v закрасим в чёрный цвет.
Может оказаться так, что две вершины v1 и v2 одного цвета соединены между собой ребром. В этом случае d(v1) = d(v2). Действительно, предположим, что d(v1) < d(v2). Тогда d(v1)+2 £ d(v2). Но поскольку v1 и v2 соединены ребром, существует маршрут, ведущий из v0 в v2 и проходящий по d(v1)+1 рёбрам: сначала он идёт по d(v1) рёбрам в v1, а потом по одному ребру из v1 в v2. Противоречие. Ребро, соединяющее вершины v1 и v2, для которых d(v1) =d(v2) закрасим в красный цвет. Покажем, что число красных рёбер не превышает 1009. Из каждой вершины v, отличной от v0, выходит хотя бы одно ребро, ведущее по направлению к v0 по кратчайшему маршруту. Такое ребро не является красным. При этом никакое ребро не может идти по кратчайшему маршруту к v0, выходя из двух различных вершин. Следовательно, количество не закрашенных в красный цвет рёбер не меньше 2015, а количество красных рёбер – не больше 1009. Удалим из графа G все красные рёбра. Каждое из оставшихся рёбер соединяет белую вершину с чёрной. Рассмотрим произвольный замкнутый маршрут. В нём чередуются белые и чёрные вершины. Количество белых вершин (с учётом кратности прохождения) равно количеству чёрных, а общее количество вершин в таком маршруте чётно. Следовательно, количество рёбер в таком маршруте чётно.
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 42; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.2.34 (0.007 с.) |
 .Но из условия
.Но из условия 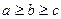 следует
следует 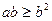 ,
, 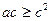 и
и  . Поэтому:
. Поэтому: 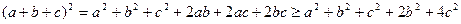 ,
,
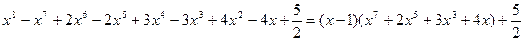
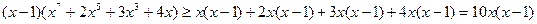
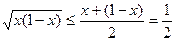 ,
,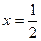 . Поэтом
. Поэтом  .
.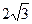 , а объём равен
, а объём равен 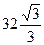 .
.
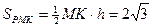 , откуда
, откуда 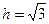 и объём пирамиды равен
и объём пирамиды равен  .
.


