
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мэ олимпиады. 11 класс. 2013годСтр 1 из 5Следующая ⇒
МЭ олимпиады. 11 Класс. 2013год 1. Противостояния Марса, то есть ситуации, когда Земля расположена между Марсом и Солнцем, происходят каждые 780 земных суток. Определить период обращения Марса вокруг Солнца. Земной год считать равным 365,25 суток, орбиты Земли и Марса считать лежащими в одной плоскости. 2. Пусть x1, x2, …, xn – попарно различные положительные числа, n ≥ 3. Доказать, что среди них можно выбрать такие два числа xi и xj, что
3. Длины сторон треугольника являются корнями уравнения x3 + ax2 + bx +c = 0. Найти площадь треугольника. 4. Какова наибольшая площадь ортогональной проекции единичного куба на плоскость? 5. Двенадцать карандашей заточены так, что все они имеют разные длины. Маша хочет положить карандаши в коробку в два ряда по 6 штук в ряд так, чтобы в каждом ряду длины карандашей убывали слева направо, и каждый карандаш из второго ряда лежал на более длинном карандаше. Сколькими способами она может это сделать? МЭ олимпиады. 11 Класс. 2015год 1. Положительные числа 2. На плоскости расположены пять квадратов так, что любые два из них имеют непустое пересечение. Обязательно ли среди них найдутся три квадрата, имеющие общую точку? 3. Сколько действительных решений имеет уравнение
4. В основании четырёхугольной пирамиды PABCD лежит квадрат ABCD со стороной 4. Известно, что среди боковых граней есть правильный треугольник и есть прямоугольный треугольник. Найти все возможные значения объёма такой пирамиды. 5. В Графландии 2016 городов, которые соединены дорогами так, что из любого города можно проехать по этим дорогам в любой другой город, причём из каждого города выходит ровно по три дороги. Королю захотелось сократить число дорог, перекрыв движение по некоторым из них. Доказать, что он может перекрыть не больше 1009 дорог так, что в стране не останется замкнутых маршрутов с нечётным числом дорог. Под маршрутом понимается путь по дорогам из города в город, не проходящий дважды по одной дороге. Маршрут называется замкнутым, если его начало и конец совпадают. МЭ. Решения. 11 класс. 2013год 1. За период между двумя противостояниями проходит больше двух земных лет. Точнее, 780/365,25 = 2,135 лет. За это время Марс делает вокруг Солнца ровно на один круг меньше. Значит, 780 земных суток составляют 1,135 марсианского года. В итоге, один год на Марсе составляет 780/1,135 = 687,22 суток.
Ответ. 687 земных суток. 2. Пусть xi = tg αi, где 0 < αi < π/2. Будем считать, что x1 < x2 < … < xn. Тогда числа α2 – α1, α3 – α2, α4 – α3, …, αn – αn–1 положительны, и их сумма меньше π/2. Всего в этом ряду (n – 1) чисел, значит одно из них (к примеру, αi+1 – αi) меньше 3. По формуле Герона для площади получаем: S2 = p(p – x1)(p – x2)(p – x3), где x1, x2, x3 – длины сторон треугольника, которые являются решениями данного уравнения, p – полупериметр треугольника. Само уравнение при этом можно переписать в виде (x – x1)(x – x2)(x – x3) = 0. Раскрывая скобки и приравнивая коэффициенты в двух версиях уравнения, получаем равенства a = – (x1 + x2 + x3) = –2p; p = – a/2; p – a = – 3a/2; p – b = – a/2 – b; p – c = – a/2 – c. Подставляя полученные выражения в формулу Герона, получаем, учитывая изменение знаков при умножении:
Ответ: 4. Центр куба является его центром симметрии. Рёбра куба можно разбить на три класса, в каждый класс попадают параллельные друг другу рёбра. При ортогональном проектировании куба на плоскость в произвольном направлении все рёбра одного класса изображаются параллельными друг другу отрезками. Результат проектирования – выпуклый центрально симметричный многоугольник, стороны которого параллельны не более чем трём направлениям. Таким многоугольником может быть либо параллелограмм, либо центрально симметричный шестиугольник. Проекцию в виде параллелограмма (который всегда будет прямоугольником) можно рассматривать как вырожденный случай проекции в виде шестиугольника, две пары сторон которого дополняют друг друга до двух отрезков.
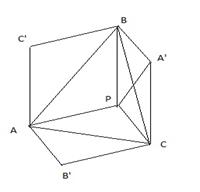
Пусть ABCA’B’C’ – такой шестиугольник. Обозначим P точку, симметричную точке A’ относительно середины отрезка [BC]. Четырёхугольник BA’CP – параллелограмм, так как его диагонали в точке пересечения делятся пополам. Значит [PC] || [BA’] || [AB’] и |PC| = |BA’| = |AB’|, четырёхугольник PCB’A является параллелограммом, и точки P и B’ симметричны относительно середины отрезка [AC]. Аналогично, четырёхугольник AC’BP является параллелограммом, и точки P и C’ симметричны относительно середины отрезка [AB]. Следовательно, площадь шестиугольника равна удвоенной площади треугольника ABC. При ортогональном проектировании произвольного многоугольника площадь проекции не превышает площади самого многоугольника. Равенство возможно только в том случае, когда направление проектирования перпендикулярно плоскости многоугольника. Получаем, что максимальную площадь имеет проекция куба в направлении его диагонали. Она равна
Ответ: 5. Укладку карандашей, удовлетворяющую условиям в задаче, будем называть правильной. Будем складывать карандаши в коробку в порядке убывания длин. При этом порядок вложения будем фиксировать в виде ломаного маршрута из точки (0,0) в прямоугольной декартовой системе координат плоскости в точку (6,6). Маршрут будем строить по следующим правилам. Если карандаш кладётся в нижний ряд, то мы проводим очередное звено ломаной длины 1 сонаправленно с осью Ox, если карандаш кладётся во второй ряд, то мы проводим звено длины 1 сонаправленное с осью Oy. В итоге получается ломаный маршрут из 12 звеньев, каждое звено которого имеет единичную длину, сонаправлено с одной из координатных осей, причём для каждой из осей есть ровно 6 сонаправленных с ней звеньев. Кроме того, для каждого узла с координатами (x, y) выполняется неравенство x ≥ y. Такой маршрут также называем правильным, а узлы, через которые может проходить правильный маршрут, называем допустимыми. Каждой правильной укладке однозначно сопоставляется правильный маршрут. Верно и обратное: каждому правильному маршруту однозначно сопоставляется правильная укладка карандашей. Таким образом, необходимо найти число правильных ломаных маршрутов из начала координат в точку (6,6). Все такие маршруты расположены внутри квадрата со стороной 6, стороны которого лежат на координатных осях или параллельны им. Выполним чертёж квадрата, отмечая узлы координатной сетки. Допустимые узлы отмечаем кружком, в котором поставим число возможных продолжений маршрута из отмеченного узла до конца. Узел с координатами (6,6), соответствующий концу всех правильных маршрутов, отмечаем числом 1. Правило, по которому заполняются последующие значения: в отмеченный узел (x, y) ставится число, равное сумме чисел в узлах (x+1, y) и (x, y+1), если эти узлы допустимы. Заполнение диаграммы происходит последовательно из правого верхнего угла в левый нижний. Заполненная диаграмма представлена на рисунке.
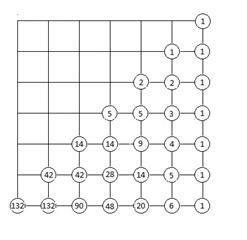
Число 132 в левом нижнем углу рисунка – ответ на вопрос задачи. Ответ: 132. Ответ: нет. 3. Представим левую часть в виде
Если x не принадлежит интервалу (0, 1), то левая часть заведомо положительна. Сделаем оценку при 0 < x < 1.
В силу неравенства между средним арифметическим и средним геометрическим имеем
причём равенство достигается только при Равенство возможно лишь при Ответ: ни одного. 4. Среди боковых граней пирамиды есть правильный треугольник. Можно считать, что это треугольник PAB. Пусть PM – его медиана, которая также является и его высотой. Тогда пирамида симметрична относительно плоскости, содержащей PM и перпендикулярной к AB.
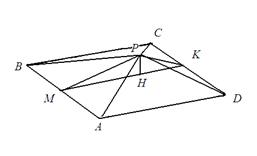
Рассмотрим возможное расположение боковой грани, которая является прямоугольным треугольником. Она может примыкать к грани PAB, или лежать напротив неё. В первом случае оба треугольника PAD и PBC являются прямоугольными. Прямыми углами в этих треугольниках могут быть только углы PAD и PBC. Высота такой пирамиды совпадает с отрезком PM и равна
Во втором случае прямоугольный треугольник PCD является равнобедренным, и прямой угол – это угол при вершине S. Высота PK такого треугольника является также его медианой и равна 2. Высота пирамиды совпадает с высотой треугольника PMK, опущенной из вершины P.
Находя площадь треугольника PMK по формуле Герона, получаем Ответ: 5. Построим граф G, вершины которого соответствуют городам, а рёбра – дорогам. По условию граф является связным и из любой вершины выходит ровно три ребра. Число рёбер графа G равно 3024. Закрасим вершины G в два цвета следующим образом. Выберем произвольную вершину v0 и закрасим её в белый цвет. Остальные вершины будем закрашивать по следующему правилу. Для произвольной вершины v обозначим d(v) число дорог в маршруте, ведущем из v0 в v и проходящем по наименьшему числу дорог. Вершину v закрасим в белый цвет в том и только том случае, когда число d(v) чётно. В случае, когда d(v) нечётно, вершину v закрасим в чёрный цвет. Может оказаться так, что две вершины v1 и v2 одного цвета соединены между собой ребром. В этом случае d(v1) = d(v2). Действительно, предположим, что d(v1) < d(v2). Тогда d(v1)+2 £ d(v2). Но поскольку v1 и v2 соединены ребром, существует маршрут, ведущий из v0 в v2 и проходящий по d(v1)+1 рёбрам: сначала он идёт по d(v1) рёбрам в v1, а потом по одному ребру из v1 в v2. Противоречие. Ребро, соединяющее вершины v1 и v2, для которых d(v1) =d(v2) закрасим в красный цвет. Покажем, что число красных рёбер не превышает 1009. Из каждой вершины v, отличной от v0, выходит хотя бы одно ребро, ведущее по направлению к v0 по кратчайшему маршруту. Такое ребро не является красным. При этом никакое ребро не может идти по кратчайшему маршруту к v0, выходя из двух различных вершин. Следовательно, количество не закрашенных в красный цвет рёбер не меньше 2015, а количество красных рёбер – не больше 1009. Удалим из графа G все красные рёбра. Каждое из оставшихся рёбер соединяет белую вершину с чёрной. Рассмотрим произвольный замкнутый маршрут. В нём чередуются белые и чёрные вершины. Количество белых вершин (с учётом кратности прохождения) равно количеству чёрных, а общее количество вершин в таком маршруте чётно. Следовательно, количество рёбер в таком маршруте чётно.
Ответ: Незнайка ошибается.
2. Пусть а поделив на a, получим: Складывая, приходим к оценке: Но для положительных чисел a и b выполнено неравенство
Ответ: а) Нет, б) Нет.
4. Преобразуем уравнение к виду
и в итоге: Последнее уравнение эквивалентно системе: Из второго уравнения Ответ: 0. 5. Будем называть центральной клеткой Т-тетрамино клетку, к которой примыкают все остальные. Для того, чтобы Т-тетрамино накрыло Машин прямоугольник, необходимо, чтобы его длинная планка целиком легла на этот прямоугольник. При этом центральная клетка Т-тетрамино ложится на центральную клетку Машиного прямоугольника. Если Т-тетрамино накрывает Вовин прямоугольник, центральная клетка Т-тетрамино является одной из двух накрывающих клеток. Центральные клетки Машиных прямоугольников могут занять любое из 60 положений (мы должны исключить четыре угловых клетки доски). Маша заняла 21 из этих 60 клеток. Вовины прямоугольники занимают 44 клетки, из них 4 могут оказаться угловыми, остальные 40 – не угловые. По принципу Дирихле найдётся не угловая клетка, накрытая центральной клеткой Машиного прямоугольника и одной из клеток Вовиного прямоугольника. Назовём такие два прямоугольника выделенными. Положим Т-тетрамино так, чтобы его перекладина легла на выделенный Машин прямоугольник, и одна из трёх нецентральных клеток Т-тетрамино накрывала оставшуюся клетку выделенного Вовиного прямоугольника. Задача решена.
Ответ: нет.
Ответ: Да. 5. Покажем, что число братьев должно равняться числу сестёр. Пусть имеется m братьев и n сестёр. Поскольку сейчас все братья в ссоре с разным числом сестёр, значит, есть хотя бы одна пара, которая всё ещё находится в ссоре. Поскольку сейчас каждая сестра находится в ссоре с одним и тем же числом братьев, значит каждая в ссоре хотя бы с одним из них, и час назад она с этим братом тоже была в ссоре. Но час назад сёстры были в ссоре с разным числом братьев. Обозначим ai число братьев, бывших в ссоре с i-й сестрой час назад. Все числа a1, …, an – это различные натуральные числа, не превосходящие m., следовательно, n ≤ m (число сестёр не больше, чем число братьев). С другой стороны, час назад каждая сестра была в ссоре с разным числом братьев, следовательно, одна из сестёр не была в ссоре хотя бы с одним братом. Братья же были в ссоре с одинаковым числом сестёр, значит, каждый не был в ссоре хотя бы с одной из них. После примирения число ссорящихся пар уменьшилось, и теперь по-прежнему каждый из братьев не в ссоре хотя бы с одной из сестёр. Обозначим bj число сестёр, с которыми находится в ссоре брат с номером j. Числа b1, …, bm – различные целые не отрицательные числа, не превосходящие n – 1, следовательно, m ≤ n (число братьев не больше, чем число сестёр). Утверждение доказано, равенство m = n является истинным. Осталось найти возможные значения для числа m = n. Как видно из предыдущего рассуждения, час назад была сестра, которая была в ссоре ровно с одним братом. Значит, после примирения каждая из сестёр находится в ссоре ровно с одним братом. Общее число ссорящихся пар равно n. И при этом число ссорящихся пар равно n = 0 + 1 + … + (n – 1), откуда n = 3. Приведём пример, показывающий, что такая ситуация возможна. Обозначим братьев буквами A, B, C, а сестёр – цифрами 1, 2, 3. Запись вида A3 будет означать, что брат A в ссоре с сестрой 3. Пусть множество пар в ссоре час назад было {A1, A3, B2, B3, C2, C3}, а после примирения – {A1, C2, C3}. Легко видеть, что в этом примере условия выполняются. Замечание. Если дан только ответ без обоснования, 0 баллов. Если приведён пример без доказательства равенств m = n = 3, 1 балл. МЭ олимпиады. 11 Класс. 2013год 1. Противостояния Марса, то есть ситуации, когда Земля расположена между Марсом и Солнцем, происходят каждые 780 земных суток. Определить период обращения Марса вокруг Солнца. Земной год считать равным 365,25 суток, орбиты Земли и Марса считать лежащими в одной плоскости. 2. Пусть x1, x2, …, xn – попарно различные положительные числа, n ≥ 3. Доказать, что среди них можно выбрать такие два числа xi и xj, что
3. Длины сторон треугольника являются корнями уравнения x3 + ax2 + bx +c = 0. Найти площадь треугольника. 4. Какова наибольшая площадь ортогональной проекции единичного куба на плоскость? 5. Двенадцать карандашей заточены так, что все они имеют разные длины. Маша хочет положить карандаши в коробку в два ряда по 6 штук в ряд так, чтобы в каждом ряду длины карандашей убывали слева направо, и каждый карандаш из второго ряда лежал на более длинном карандаше. Сколькими способами она может это сделать?
|
|||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 42; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.77.195 (0.037 с.) |
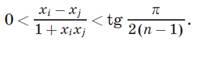
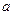 ,
, 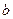 и
и 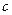 таковы, что
таковы, что 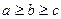 и
и 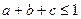 . Докажите, что
. Докажите, что 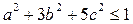
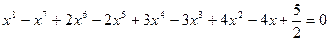 ?
? . Применив к числам xi и xi+1 формулу тангенса разности, получим требуемые неравенства.
. Применив к числам xi и xi+1 формулу тангенса разности, получим требуемые неравенства.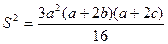 и
и 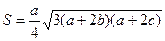 .
.
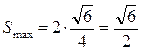
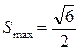 .
.
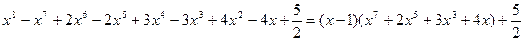
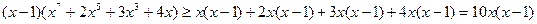
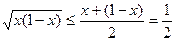 ,
,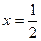 . Поэтом
. Поэтом  .
.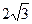 , а объём равен
, а объём равен 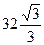 .
.
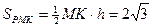 , откуда
, откуда 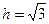 и объём пирамиды равен
и объём пирамиды равен  .
.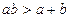 . Поделив на b, получим:
. Поделив на b, получим: 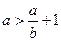 ,
, .
.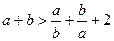 .
. , откуда и получаем требуемый результат.
, откуда и получаем требуемый результат. 3. а) Предположим, что указанный отрезок является высотой. Тогда центр вписанной окружности лежит на серединном перпендикуляре к высоте, а радиус вписанной окружности равен половине высоты. Получается, что одна из касательных, проведённых из вершины, параллельна основанию. Треугольник не образуется: в треугольнике не может быть параллельных сторон.
3. а) Предположим, что указанный отрезок является высотой. Тогда центр вписанной окружности лежит на серединном перпендикуляре к высоте, а радиус вписанной окружности равен половине высоты. Получается, что одна из касательных, проведённых из вершины, параллельна основанию. Треугольник не образуется: в треугольнике не может быть параллельных сторон.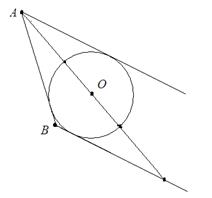 б) Предположим, что указанный отрезок является биссектрисой. Биссектриса проходит через центр вписанной окружности. Из условия следует, что касательная к вписанной окружности, которая содержит основание треугольника, симметрична прямой, содержащей одну из боковых сторон относительно центра вписанной окружности. Поэтому эти две стороны лежат на параллельных прямых. Вновь треугольник не образуется, так как прямые, которые должны содержать две его стороны, параллельны.
б) Предположим, что указанный отрезок является биссектрисой. Биссектриса проходит через центр вписанной окружности. Из условия следует, что касательная к вписанной окружности, которая содержит основание треугольника, симметрична прямой, содержащей одну из боковых сторон относительно центра вписанной окружности. Поэтому эти две стороны лежат на параллельных прямых. Вновь треугольник не образуется, так как прямые, которые должны содержать две его стороны, параллельны.
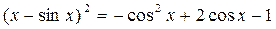
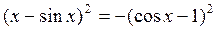 .
. .
. . При таких значениях x выполняется sin x = 0. Следовательно, первое уравнение может выполняться только при x = 0.
. При таких значениях x выполняется sin x = 0. Следовательно, первое уравнение может выполняться только при x = 0.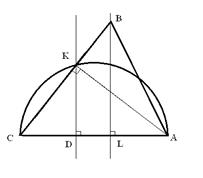 4. Покажем, как можно построить требуемый треугольник. Построим на плоскости произвольно отрезок CA, на нём выберем точку L так, что выполнено равенство
4. Покажем, как можно построить требуемый треугольник. Построим на плоскости произвольно отрезок CA, на нём выберем точку L так, что выполнено равенство 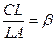 , и на отрезке CL выберем точку D так, что
, и на отрезке CL выберем точку D так, что 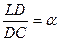 . В точках L и D построим перпендикуляры к AC: прямую p ^ AC через точку L и прямую q ^ AC через точку D. Окружность w с диаметром AC пересекает прямую q в двух точках. Обозначим одну из них K. Пусть B – точка пересечения прямых p и CK. По теореме Фалеса
. В точках L и D построим перпендикуляры к AC: прямую p ^ AC через точку L и прямую q ^ AC через точку D. Окружность w с диаметром AC пересекает прямую q в двух точках. Обозначим одну из них K. Пусть B – точка пересечения прямых p и CK. По теореме Фалеса 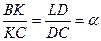 . Угол AKC – прямой, как вписанный угол, опирающийся на диаметр. Отрезок AK является высотой. Поскольку точка пересечения высот треугольника ABC находится внутри треугольника, он – остроугольный. Следовательно, треугольник ABC – искомый.
. Угол AKC – прямой, как вписанный угол, опирающийся на диаметр. Отрезок AK является высотой. Поскольку точка пересечения высот треугольника ABC находится внутри треугольника, он – остроугольный. Следовательно, треугольник ABC – искомый.


