Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мэ олимпиады. 11 класс. 2017годСодержание книги
Поиск на нашем сайте
1. Функция f(x) определена при всех действительных x, причём при любом x выполнены равенства f(x+2017)=f(2017–x) и f(x+2018)=f(2018–x). Доказать, что f – периодическая функция. 2. Решить уравнение: 3. На ледяном поле лежат три шайбы в точках A, B и C, не лежащих на одной прямой. Хоккеист толкает одну из шайб (любую) так, что она проскальзывает между двумя другими и останавливается так, что шайбы вновь образуют треугольник. Так он делает 25 раз. Может ли случиться так, что в конце каждая из шайб вернётся в начальное место? 4. Является ли истинным следующее утверждение: для любых двух положительных чисел a и b существует остроугольный треугольник ABC, высоты которого AK и BL делят противоположные стороны в отношениях a и b соответственно, то есть так, что 5. В некоторой семье есть братья и сёстры (как минимум 2 брата и как минимум 2 сестры). Час назад каждый брат в семье был в ссоре с одинаковым числом сестёр, а все сёстры были в ссоре с различным числом братьев. Но сейчас некоторые пары помирились, и теперь каждая сестра в ссоре с одинаковым числом братьев, а братья
МЭ. Решения. 11 класс. 2013год 1. За период между двумя противостояниями проходит больше двух земных лет. Точнее, 780/365,25 = 2,135 лет. За это время Марс делает вокруг Солнца ровно на один круг меньше. Значит, 780 земных суток составляют 1,135 марсианского года. В итоге, один год на Марсе составляет 780/1,135 = 687,22 суток. Ответ. 687 земных суток. 2. Пусть xi = tg αi, где 0 < αi < π/2. Будем считать, что x1 < x2 < … < xn. Тогда числа α2 – α1, α3 – α2, α4 – α3, …, αn – αn–1 положительны, и их сумма меньше π/2. Всего в этом ряду (n – 1) чисел, значит одно из них (к примеру, αi+1 – αi) меньше 3. По формуле Герона для площади получаем: S2 = p(p – x1)(p – x2)(p – x3), где x1, x2, x3 – длины сторон треугольника, которые являются решениями данного уравнения, p – полупериметр треугольника. Само уравнение при этом можно переписать в виде (x – x1)(x – x2)(x – x3) = 0. Раскрывая скобки и приравнивая коэффициенты в двух версиях уравнения, получаем равенства a = – (x1 + x2 + x3) = –2p; p = – a/2; p – a = – 3a/2; p – b = – a/2 – b; p – c = – a/2 – c. Подставляя полученные выражения в формулу Герона, получаем, учитывая изменение знаков при умножении:
Ответ: 4. Центр куба является его центром симметрии. Рёбра куба можно разбить на три класса, в каждый класс попадают параллельные друг другу рёбра. При ортогональном проектировании куба на плоскость в произвольном направлении все рёбра одного класса изображаются параллельными друг другу отрезками. Результат проектирования – выпуклый центрально симметричный многоугольник, стороны которого параллельны не более чем трём направлениям. Таким многоугольником может быть либо параллелограмм, либо центрально симметричный шестиугольник. Проекцию в виде параллелограмма (который всегда будет прямоугольником) можно рассматривать как вырожденный случай проекции в виде шестиугольника, две пары сторон которого дополняют друг друга до двух отрезков.
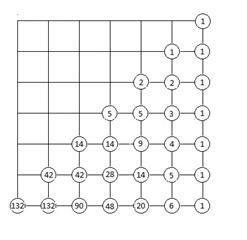
Пусть ABCA’B’C’ – такой шестиугольник. Обозначим P точку, симметричную точке A’ относительно середины отрезка [BC]. Четырёхугольник BA’CP – параллелограмм, так как его диагонали в точке пересечения делятся пополам. Значит [PC] || [BA’] || [AB’] и |PC| = |BA’| = |AB’|, четырёхугольник PCB’A является параллелограммом, и точки P и B’ симметричны относительно середины отрезка [AC]. Аналогично, четырёхугольник AC’BP является параллелограммом, и точки P и C’ симметричны относительно середины отрезка [AB]. Следовательно, площадь шестиугольника равна удвоенной площади треугольника ABC. При ортогональном проектировании произвольного многоугольника площадь проекции не превышает площади самого многоугольника. Равенство возможно только в том случае, когда направление проектирования перпендикулярно плоскости многоугольника. Получаем, что максимальную площадь имеет проекция куба в направлении его диагонали. Она равна Ответ: 5. Укладку карандашей, удовлетворяющую условиям в задаче, будем называть правильной. Будем складывать карандаши в коробку в порядке убывания длин. При этом порядок вложения будем фиксировать в виде ломаного маршрута из точки (0,0) в прямоугольной декартовой системе координат плоскости в точку (6,6). Маршрут будем строить по следующим правилам. Если карандаш кладётся в нижний ряд, то мы проводим очередное звено ломаной длины 1 сонаправленно с осью Ox, если карандаш кладётся во второй ряд, то мы проводим звено длины 1 сонаправленное с осью Oy. В итоге получается ломаный маршрут из 12 звеньев, каждое звено которого имеет единичную длину, сонаправлено с одной из координатных осей, причём для каждой из осей есть ровно 6 сонаправленных с ней звеньев. Кроме того, для каждого узла с координатами (x, y) выполняется неравенство x ≥ y. Такой маршрут также называем правильным, а узлы, через которые может проходить правильный маршрут, называем допустимыми. Каждой правильной укладке однозначно сопоставляется правильный маршрут. Верно и обратное: каждому правильному маршруту однозначно сопоставляется правильная укладка карандашей. Таким образом, необходимо найти число правильных ломаных маршрутов из начала координат в точку (6,6). Все такие маршруты расположены внутри квадрата со стороной 6, стороны которого лежат на координатных осях или параллельны им. Выполним чертёж квадрата, отмечая узлы координатной сетки. Допустимые узлы отмечаем кружком, в котором поставим число возможных продолжений маршрута из отмеченного узла до конца. Узел с координатами (6,6), соответствующий концу всех правильных маршрутов, отмечаем числом 1. Правило, по которому заполняются последующие значения: в отмеченный узел (x, y) ставится число, равное сумме чисел в узлах (x+1, y) и (x, y+1), если эти узлы допустимы. Заполнение диаграммы происходит последовательно из правого верхнего угла в левый нижний. Заполненная диаграмма представлена на рисунке.
Число 132 в левом нижнем углу рисунка – ответ на вопрос задачи. Ответ: 132.
|
||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

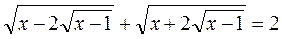
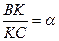 и
и 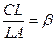 ?
? . Применив к числам xi и xi+1 формулу тангенса разности, получим требуемые неравенства.
. Применив к числам xi и xi+1 формулу тангенса разности, получим требуемые неравенства.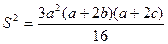 и
и 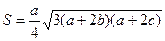 .
.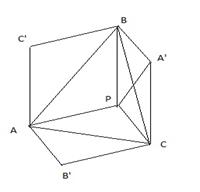
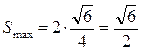
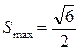 .
.