Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи математичної статистикиСодержание книги
Поиск на нашем сайте
Тема: Варіаційний ряд. Статистичний ряд. Генеральна сукупність, вибірка. Полігон і гістограма. Статистичні та інтервальні оцінки параметрів розподілу генеральної сукупності.
Мета: Закріпити та вдосконалити знання набуті на лекціях з даної теми та самостійно опрацьовувати їх з додатковою літературою. Навчитися складати варіаційний ряд, будувати гістограми та надавати числові характеристики сукупності: вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення, виправлену середню дисперсію, моду та медіану. Знати що таке довірчий інтервал, довірча ймовірність або надійність, точність оцінки. Навчитися розв’язувати задачі прикладного характеру.
Теоретичне обґрунтування Статистична сукупність – множина однорідних предметів, або явищ, об’єднаних за будь-якою ознакою. Вибірковою сукупністю, або вибіркою називається множина числових значень деякої ознаки всіх об’єктів, випадково вибраних із всієї сукупності розглянутих об’єктів.
Означення. Значення які отримали в наслідок спостережень називають варіантами, а послідовність варіант в порядку зростання називають варіаційним рядом або вибірковим.
Побудова звичайного варіантного ряду. У таблицю записують окремі значення варіант у порядку зростання, а поруч з ними, записують числа, які показують скільки разів дана варіанта зустрічається в статистичній сукупності (частота варіанти).
i = 1,2,3,... n
хi – варіанта;
mi – частота варіанти;
Означення. Лінія, відрізки якої з’єднують точки (хi; mi) називається полігоном частот.
Числові характеристики варіаційного ряду
1.2.1 Середнє арифметичне
1.2.2 Дисперсія, ДВ, це середня арифметична квадратів відхилень варіант від їх середньої арифметично
1.2.3 Середнє квадратичне відхилення
Середнє квадратичне відхилення ( Означення. Модою (Мо) називають варіанту, яка має найбільшу частоту.
Означення. Медіаною (Ме) називають варіанту, яка ділить варіаційний ряд на дві частини, рівні по числу варіанти.
Якщо кількість варіант парне, то
1.2.4 Коефіцієнт варіації υ – це відношення стандартного відхилення до середньої вибіркової, що виражається в процентах
Інтервальний варіаційний ряд
Для побудови інтервального варіаційного ряду діапазон значень ознак
Кількість інтервалів k, розмах варіації R та довжина інтервалу h пов’язані між собою співвідношенням: R = К · h. довжина інтервалу: h = Кількість інтервалів, на які розбивається уся сукупність, залежить від об’єму сукупності.
Існує декілька способів знаходження кількості класів, але на практиці можна користуватися таблицею:
Таблиця №1 Кількість класів
Таким чином, інтервальний ряд становить з себе ряд напіввідчинених інтервалів:
Звичайно варіаційний інтервальний ряд задається таблицею:
Таблиця №2 Варіаційний інтервальний ряд
Гістограма частот – це ступенева фігура, що складається з прямокутників, основа яких – довжина інтервалу (крок інтервалу), а висота дорівнює mi.
Малюнок 1 Гістограма частот
Полігон розподілу будується так само, як у звичайного варіаційного ряду, де
Числові характеристики 1.3.1 Середнє арифметичне:
де
1.3.2 Дисперсія
Виправлена дисперсія
де
Статистичні оцінки. 1.4.1 Вибіркове середнє
1.4.2 Вибіркова дисперсія
1.4.3 Середнє квадратичне відхилення
1.4.4 Виправлена вибіркова дисперсія (для великих n)
Інтервальні оцінки
Означення: Число
1.5.1 При нормальному розподіленні випадкової величини довірчий інтервал обчислюється за формулою
де: n - об’єм вибірки
якщо n дуже велике, то довірчий інтервал:
де S – виправлене стандартне відхилення вибіркове
Розв’язування типових задач Задача 1 1 Скласти ряд розподілу довжини сардинели, яка мешкає біля узбережжя Екваторіальної Африки, за слідуючими даними (n = 100) 2 Знайти числові характеристики вибірки розподілу довжини сардинели.
Таблиця №3 Вибірка розподілу довжини сардинели
xmin=17,8, xmax=21,4 для складання варіаційного ряду розіб’ємо весь інтервал можливих значень випадкової величини на 9 розрядів, k = 9 (дивись табл.1)
Довжина інтервалу
Домовимося що кожний розряд буде включати праву границю і не буде включати ліву (виняток тільки у першому розряді). Побудову варіаційного ряду зручно вести у таблиці.
Таблиця №4 Дані для побудови гістограми
Контроль таблиці n=
Будуємо гістограму відносних частот
Малюнок 2 Гістограма відносних частот розподілу довжини сардинели
Якщо будувати гістограму частот, то висота прямокутника дорівнює щільності частоти на даному інтервалі 2 Знайдемо числові характеристики вибірки розподілу довжини сардинели.
Таблиця №5 Кількість варіант які потрапляють в заданий інтервал
Оцінимо середню вибіркову
Знайдемо дисперсію за формулою
Dв=400,32 – 202 = 0,32
Знайдемо середнє квадратичне відхилення:
Відповідь: Задача 2 За даними вибірки записати варіаційний ряд, знайти частоту варіант. 2.1 Дати оцінку: - вибіркового середнього; - вибіркової дисперсії; - середнього квадратичного відхилення; - знайти моду та медіану; 2.2 Знайти надійний інтервал для вибіркової середньої, якщо р= 0,96 (дані використовувати з попередніх розрахунків). Для заданої вибірки:
30, 38, 32, 33, 30, 33, 35, 38, 31, 37, 32, 36, 37, 31, 34, 32, 35, 38, 30, 31. Розв’язання: Складаємо варіаційний ряд і записуємо частоту кожної варіанти. Для обчислення числових характеристик записуємо розрахунки в таблиці.
Перевірка: Знайдемо середнє вибіркове:
Знайдемо вибіркову дисперсію:
Знайдемо середнє квадратичне відхилення:
Знайдемо моду і медіану: Мода – це варіанта, яка має найбільшу частоту
Знайдемо довірчий інтервал для вибіркової середньої, якщо
Відповідь: (32,354;34,946)
2 Запитання до самоконтролю 2.1 Визначити який ряд називається варіаційним? 2.2 Дайте означення гістограми. 2.3 Запишіть формулу розрахунку довжини інтервалу? 2.4 Дайте означення довірчого інтервалу. 2.5 Записати формулу точності оцінки. 2.6 Запишіть формулу довірчого інтервалу при малих вибірках. Індивідуальні завдання до самостійної роботи № 4 Задача 1 1 Скласти варіаційний ряд і накреслити гістограму розподілу обхвату тіла пеляді озера Бакул. (n = 50). 2 Знайти числові характеристики даної вибірки, знайшовши середини інтервалів Хі, варіаційного ряду. Дані взяти із таблиці №1 Таблиця №1 Вихідні дані
Таблиця № 2 Варіанти
Задача № 2
Приймаючи дані із таблиці випадкової вибірки обхвату тіла риби товстолоба знайти:
Таблиця №3 Дані обхвату тіла риби товстолоба у ставку з 1 по 10 варіанти
Таблиця №3 Дані обхвату тіла риби товстолоба у ставку з 11 по 20 варіанти
Висновок Виконання студентами самостійної роботи дає можливість студенту активно «включати» розумову діяльність, спонукає їх до самостійних роздумів, аналізу прочитаного матеріалу. Самостійна робота дає можливість використовувати різноманітні математичні методи для математичного моделювання, аналізу та оптимізації виробничих процесів рибного господарства. Література
1 Валуце І.І., Ділігул Г.Д. “Математика для технікумів”: Навч. посібник. – – М.: Наука. 1989. 576 с. 2 Аксютіна З.М.Элементи математической оценки результатов наблюдения в биологических и рыбохозяйственных исследованиях, (Р1, гл. 1-2) 3 Засуха В.А., Лисеноко В.П., Голубєва Б.Л. Прикладна математика: Підручник. – 2-ге видання, перероблене та доповнене. –К.: Арістей 2005. – 304с. 4 Гмурман В.Е. Руководство к решению задач по теориии вероятностей и математической статистике, (Р.6 п 1,2,3)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.012 с.) |

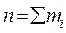 - об’єм сукупності;
- об’єм сукупності; - відносна частота.
- відносна частота.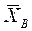
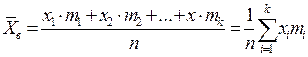 , 1.2.1
, 1.2.1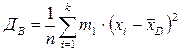 1.2.2
1.2.2 1.2.3
1.2.3 ) – являється показником розсіювання значень варіант навколо середньої арифметичної.
) – являється показником розсіювання значень варіант навколо середньої арифметичної. . 1.2.4
. 1.2.4 . 1.2.5
. 1.2.5 , який називається розмахом варіації, ділимо на k – інтервалів. Підраховуємо mi (i = 1,2,... к), яке відноситься до відповідного інтервалу і показує, скільки варіант потрапляють у даний i -тий інтервал.
, який називається розмахом варіації, ділимо на k – інтервалів. Підраховуємо mi (i = 1,2,... к), яке відноситься до відповідного інтервалу і показує, скільки варіант потрапляють у даний i -тий інтервал.  - розмах варіації.
- розмах варіації.
 де 1.2.6
де 1.2.6 .
.



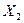


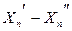


 , 1.3.1
, 1.3.1 - середини інтервалів;
- середини інтервалів; , або
, або 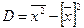 1.3.2
1.3.2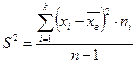 , 1.3.3
, 1.3.3 , 1.4.1
, 1.4.1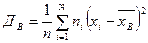 , або
, або 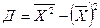 , 1.4.2
, 1.4.2
 , 1.4.3
, 1.4.3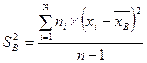 1.4.4
1.4.4 і
і  називають довірчими границями з надійною ймовірністю
називають довірчими границями з надійною ймовірністю  , а інтервал (
, а інтервал (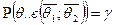 , ймовірність
, ймовірність  називається надійністю.
називається надійністю. 1.5.1
1.5.1 функція Лапласа (дивись додаток 2)
функція Лапласа (дивись додаток 2)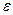 - стандартне відхилення
- стандартне відхилення - точність оцінки
- точність оцінки 1.5.2
1.5.2 - дивись додаток 3, по заданим n і γ.
- дивись додаток 3, по заданим n і γ.


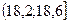







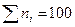


 .
.




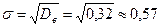
 , Dв = 0,32,
, Dв = 0,32, 



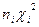


 ;
; 
 де
де 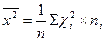 ;
;
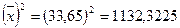

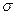





 де
де 
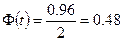 ,
,  (дивись додаток 2)
(дивись додаток 2) ;
;