
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самостійна робота № 2 ( 10 годин)Содержание книги
Поиск на нашем сайте
Тема: Класичне означення ймовірності. Теореми додавання і множення ймовірностей. Елементи комбінаторики. Незалежні події. Формула повної ймовірності та формула Байєса. Формула Бернулі. Локальна та інтегральна теореми Лапласа. Мета: Придбати навички розв¢язування задач.
Теоретичне обгрунтування Елементи комбінаторики
Перестановки. Всякий встановлений в скінченій множині порядок називається перестановкою його елементів. Позначають: Р = n! n! = n·(n - 1)·(n - 2) … Розміщення. Множина, в якій задано порядок розміщення її елементів називається упорядкованою. Нехай дано скінчену множину, яка складається з n елементів. Усяка її упорядкована m – елементна підмножина називається розміщенням з n елементів по m.
Комбінації або сполучення. Нехай дано скінчену множину, яка складається з n елементів. Усяка її m – елементна підмножина називається сполученням з n елементів по m.
1.2 Елементи теорії імовірності. Означення: Випадковою подією називається подія, яка може відбутися, або не відбутися під час здійснення певного випробування. 1.3 Означення: Вірогідною називається подія, яка в наслідок даного випробування обов¢язково має відбутися. А не можливою називається така подія, яка внаслідок даного випробування не може відбутися. 1.4 Класичне означення ймовірності. Ймовірністю випадкової події називається відношення кількості подій які сприяють цій події, до кількості всіх рівноможливих несумісних подій, які утворюють повну групу подій під час певного випробування.
Теорема додавання Означення. Сумою двох подій називається подія С, яка полягає у здійсненні під час випробування, або подія А, або події В. Теорема. Сума двох несумісних подій.
Сума двох сумісних подій
1.6 Теорема множення ймовірностей
Означення.Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробування і події А і події В.
Теорема: Добуток двох незалежних подій
1.7 Формула Бернуллі Означення. Випробування при яких ймовірність появи події А в кожному випробуванні не залежить від наслідків інших випробувань, називаються незалежними відносно події А. Формула Бернуллі:
q = 1-p
1.8 Формула повної ймовірності.
де гіпотези Н1, Н2, …, Нn утворюють повну групу подій.
1.9 Формула Байєса Якщо подія А вже відбулася то ймовірність гіпотез можуть бути переоцінені за формулою Байєса.
1.10 Локальна теорема Лапласа.
Ймовірність того, що подія А з’явиться в n незалежних іспитах рівно k раз, приблизно дорівнює.
1.11 Інтегральна теорема Лапласа Ймовірність того, що подія А з’явиться в n незалежних іспитах від k1 до k2, виражається за формулою:
де
Ф(х) – дивись додаток №2 Ф(-х) = -Ф(х) Для х › 5 можна прийняти Ф (х) = 0,5
Розв’язування типових прикладів 2.1 3 корзини, в яких є 5 білих і 3 чорних кулі, виймають одну кулю. Знайти ймовірність того, що куля буде чорною.
Розв’язання
Позначимо подію, що з корзини буде вийнято чорну кулю, через А. Загальне число випадків n = 5+3=8 Число випадків, які сприяють події А, дорівнює 3. Тоді маємо:
або 37,5 %.
2.2 Слово «ймовірність» складено із букв розрізної азбуки. Потім картки з буквами перемішують, і відкладають по черзі 8 карток. Яка ймовірність того, що ці 8 карток в порядку витягування утворять слово «вірність».
Розв’язання
Знайдемо загальну кількість рівно можливих подій. Множина карток складається із дев’яти букв розрізної азбуки, а підмножина із 8 карток є упорядкованою (в слові «вірність» враховується порядок), то даний порядок є розміщення. Маємо А число елементарних подій, які сприяють появі слова «вірність» m, дорівнює 1, m=1.
Маємо
Задача про вибірку
У партії з 10 деталей, 6 стандартні. Контролер взяв навмання 4 деталі. Обчислити ймовірність того, що хоча б одна з узятих деталей буде стандартною.
Розв’язання
Елементарним наслідком є вибір будь-яких деталей із загального числа 10. Число всіх таких наслідків дорівнює числу комбінацій з 10 по 4, тобто Подія А – із 4 деталей, одна бракована. Наслідком, який сприяє появі події А, є поява групи з 4 деталей, в якій одна стандартна. Групу бракованих деталей можна знайти: 10 – 6 = 4 (брак), тобто
Тоді
2.5 В ящику 12 деталей, з яких 8 стандартних. Робітник бере навмання дві деталі. Обчислити ймовірність того, дві деталі будуть стандартні.
Розв’язання
Подія А – перша взята деталь стандартна. В – друга взята деталь стандартна.
Ймовірність того, що обидві деталі будуть стандартними, знаходимо за теоремою множення ймовірностей залежних подій.
2.6 Ймовірність влучень в ціль з одного пострілу становить 0,8. Знайти ймовірність семи влучень при 10 пострілах.
Розв’язання
За формулою Бернуллі: n = 10, k = 7, p = 0,8, q = 1 – 0,8 =0,2
2.7 На складі надійшли деталі з трьох верстатів. На першому верстаті виготовлено 40% деталей загальної кількості, на другому - 35%, на третьому - 25%, причому на першому було виготовлено 90% деталей першого сорту, на другому - 80% і на третьому - 70%. Яка ймовірність того, що взята навмання деталь буде першого сорту?
Розв’язання
Позначимо події Н1 - деталь виготовлена на першому верстаті, Н2 – на другому, Н3 - на третьому. Подія А - деталь першого сорту.
Ймовірність - деталь першого сорту
Тобто за формулою повної ймовірності:
2.8 Знайти ймовірність того, що подія А відбудеться рівно 70 раз в 243 іспитах, якщо ймовірність появи цієї події в кожному іспиті = 0,25.
Розв’язання: За умовою, n =243, k = 70, р = 0,254; q=0,75. Так як n=243 – достатньо велике число, скористуємося локальною теоремою Лапласа.
див. Додаток 1, φ(1,37)=0,1561
маємо:
Відповідь: 0,0231
2.9 Ймовірність появи події в кожному із 100 незалежних іспитів дорівнює 0,8. Знайти ймовірність того, що подія відбувається не менше 75 разів і не більше 90 разів. Розв’язання: за інтегральною теоремою Лапласа
за умовою: n = 100; p =0.8; q = 0.2;
див. Додаток 2. Ф (-1,25) = -Ф(1,25)= - 0,3944 Ф(2,5) = 0,4938
Маємо Р
Відповідь: 0,8882 3 Запитання для самоконтролю 3.1 Дати означення ймовірності. 3.2 Назвіть, які події називаються несумісними і сумісними. 3.3 Визначте, що називається сумою двох подій та добутком. 3.4 Запишіть формулу повної ймовірності та формулу Байєса. 3.5 Запишіть формулу Бернуллі. 3.6 Запишіть локальну та інтегральну теореми Лапласа.
Індивідуальні завдання до самостійної роботи №2
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.58 (0.009 с.) |




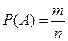



 ,
,

 ,
,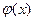 - дивись додаток №1
- дивись додаток №1
 ,
,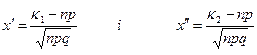

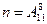

 ,
, 
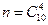 .
. , а групу стандартних деталей
, а групу стандартних деталей  , так як ці події виконуються одночасно, то наслідки які сприяють появі події А дорівнюють
, так як ці події виконуються одночасно, то наслідки які сприяють появі події А дорівнюють  .
.






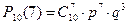



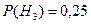
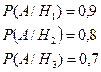

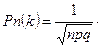 φ(х),
φ(х),

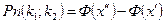 ,
, ;
;  ,
, ;
; 


 (75;90) = 0,4938+0,3944 = 0,8882
(75;90) = 0,4938+0,3944 = 0,8882


