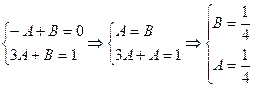Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основи прикладної математикиСодержание книги
Поиск на нашем сайте
Основи прикладної математики
Методичні вказівки до самостійної роботи студентів Спеціальності 5.09020101 “Рибництво і аквакультура”
Укладач: Рачицька Тетяна Федорівна - викладач методист Білгород – Дністровського державного морського рибопромислового технікуму Методичні вказівки розглянуті та рекомендовані у навчальний процес цикловою комісією природничо-математичних дисциплін
Протокол № від ___ __________ 2011 року
Голова циклової комісії Лісогор Н.І.
ВСТУП
На вивчення даної дисципліни відводиться 81 година: з них 40 годин аудиторних і 41 година на самостійну роботу студентів. Мета та задача методичних вказівок до кожної роботи полягає в тому, щоб студент міг самостійно виконати індивідуальні завдання, користуючись вказівками та розв’язуванням типових задач і закріпити та вдосконалити свої знання набуті на лекціях. Навчитися самостійно працювати з додатковою літературою, робити висновки з самостійно розглянутих і вивчених розділів.
Оцінювання кожної роботи проводиться за п’ятибальною шкалою.. Якщо студент виконав менше 50% завдання, робота оцінюється на “2”; якщо від 50% до 75%, оцінка – “3”; якщо від 76% до 95%, оцінка – “4”; якщо більше 95%, оцінка – “5”. Самостійні роботи перевіряються після закінчення логічно-завершеної частини лекції та практичних робіт. Їх результати враховуються при виставленні підсумкової оцінки. Самостійні робота виконується в зошитах в клітинку на 24 аркушах. Перелік самостійних робіт
Самостійна робота №1 Елементи вищої математики – 10 години
Самостійна робота №2 Елементи теорії ймовірності – 10 годин Теми:. Класичне означення ймовірності. Теореми додавання і множення ймовірностей. Незалежні події. Формула повної ймовірності та формула Байєса. Формула Бернуллі. Локальна і інтегральна теорема Лапласа. Самостійна робота №3 Елементи теорії ймовірності - 11 годин Теми: Повторні події.. Випадкові величини. Дискретні випадкові величини та закон розподілу випадкової величини. Числові характеристики дискретної випадкової величини. Функція розподілу випадкової величини. Щільність розподілу. Числові характеристики неперервних випадкових величин. Нормальне розподілення, його числові характеристики.
Самостійна робота №4 Елементи математичної статистики – 10 годин Тема Варіаційний ряд. Статистичний ряд. Генеральна сукупність, вибірка. Полігон і гістограма. Статистичні та інтервальні оцінки параметрів розподілу генеральної сукупності.
Тема: Елементи вищої математики Мета: Повторення та удосконалення знань та вмінь набутих в курсі середньої школи з тем: “Похідна та її застосування”, “Визначений та невизначений інтеграл”. Теоретичне обґрунтування 1.1 Правила та формули диференціювання. Правила:
Формули:
1 2 3 4 5 6 7 8 9 10 11 12
1.2 Ознаки зростання та спадання функції. Екстремуми функції.
Теорема 1 Необхідна умова зростання. Якщо функція Теорема 2 Необхідна умова існування екстремуму. Якщо точка Теорема 3 Достатня умова існування екстремуму. Нехай функція 1 Якщо похідна 2 Якщо похідна
1.3 Таблиця інтегралів
1 2 3 4 5 6 7 8 9 10 11
Формула Ньютона – Лейбніца
де а – нижня границя; в – верхня границя; F(х) – первісна. Розв’язування типових задач Дано функції
Знайти: 1 2 дослідити функцію 3 обчислити невизначений інтеграл 4 обчислити визначений інтеграл: 4.1 5 обчислити площу фігури, обмеженої лініями Розв’язання
1
2 Дослідимо функцію на зростання, спадання та точки екстремуму 2.1 ОДЗ: х
2.2 Точки перетину з віссю ох: у = 0
х = 1, х = -1, х = 2, х = -2, серед цілих чисел коренів немає. Точки перетину з віссю оу: х = 0
2.3 Знайдемо похідну
2.4 Знайдемо критичні точки
За теоремою Вієта:
2.5 Розіб’ємо область визначення функції на інтервали і знайдемо знак похідної на кожному з них.
Висновок: функція зростає на функція спадає на в т.ч. х = – 2, існує max в т.ч. х = 1, існує min
2.6 Будуємо графік функції
Малюнок 1.1 Графік функції 3 Знайдемо
4 Обчислимо інтеграл
4.2
5 Знайдемо площу фігури, обмеженої лініями y=q(x) і віссю ox.
Малюнок 1.2 – Криволінійна трапеція, обмежена лініями
Питання для самоконтролю 3.1 Чому дорівнює похідна суми? 3.2 Чому дорівнює похідна дробу? 3.3 Чому дорівнює похідна добутку? 3.4 Ознаки зростання і спадання функції. Екстремум функції, 2 умови. 3.5 Як записується формула Ньютона – Лейбніца? 3.6 Геометричний зміст визначеного інтеграла. Індивідуальні завдання до самостійної роботи № 1 Знайти: 1 похідну 2 дослідити функцію 3 невизначений інтеграл 4 визначений інтеграл: 4.1 4.2 5 обчислити площу фігури, обмеженої лініями у=q(x) і віссю ох. Таблиця 1 Варіанти
Теоретичне обгрунтування Елементи комбінаторики
Перестановки. Всякий встановлений в скінченій множині порядок називається перестановкою його елементів. Позначають: Р = n! n! = n·(n - 1)·(n - 2) … Розміщення. Множина, в якій задано порядок розміщення її елементів називається упорядкованою. Нехай дано скінчену множину, яка складається з n елементів. Усяка її упорядкована m – елементна підмножина називається розміщенням з n елементів по m.
Теорема додавання Означення. Сумою двох подій називається подія С, яка полягає у здійсненні під час випробування, або подія А, або події В. Теорема. Сума двох несумісних подій.
Сума двох сумісних подій
1.6 Теорема множення ймовірностей
Означення.Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробування і події А і події В.
Теорема: Добуток двох незалежних подій
1.7 Формула Бернуллі Означення. Випробування при яких ймовірність появи події А в кожному випробуванні не залежить від наслідків інших випробувань, називаються незалежними відносно події А. Формула Бернуллі: q = 1-p
1.8 Формула повної ймовірності.
де гіпотези Н1, Н2, …, Нn утворюють повну групу подій.
1.9 Формула Байєса Якщо подія А вже відбулася то ймовірність гіпотез можуть бути переоцінені за формулою Байєса.
1.10 Локальна теорема Лапласа.
Ймовірність того, що подія А з’явиться в n незалежних іспитах рівно k раз, приблизно дорівнює.
1.11 Інтегральна теорема Лапласа Ймовірність того, що подія А з’явиться в n незалежних іспитах від k1 до k2, виражається за формулою:
де
Ф(х) – дивись додаток №2 Ф(-х) = -Ф(х) Для х › 5 можна прийняти Ф (х) = 0,5
Задача про вибірку
У партії з 10 деталей, 6 стандартні. Контролер взяв навмання 4 деталі. Обчислити ймовірність того, що хоча б одна з узятих деталей буде стандартною.
Розв’язання
Елементарним наслідком є вибір будь-яких деталей із загального числа 10. Число всіх таких наслідків дорівнює числу комбінацій з 10 по 4, тобто Подія А – із 4 деталей, одна бракована. Наслідком, який сприяє появі події А, є поява групи з 4 деталей, в якій одна стандартна. Групу бракованих деталей можна знайти: 10 – 6 = 4 (брак), тобто Тоді
2.5 В ящику 12 деталей, з яких 8 стандартних. Робітник бере навмання дві деталі. Обчислити ймовірність того, дві деталі будуть стандартні.
Розв’язання
Подія А – перша взята деталь стандартна. В – друга взята деталь стандартна.
Ймовірність того, що обидві деталі будуть стандартними, знаходимо за теоремою множення ймовірностей залежних подій.
2.6 Ймовірність влучень в ціль з одного пострілу становить 0,8. Знайти ймовірність семи влучень при 10 пострілах.
Розв’язання
За формулою Бернуллі: n = 10, k = 7, p = 0,8, q = 1 – 0,8 =0,2
2.7 На складі надійшли деталі з трьох верстатів. На першому верстаті виготовлено 40% деталей загальної кількості, на другому - 35%, на третьому - 25%, причому на першому було виготовлено 90% деталей першого сорту, на другому - 80% і на третьому - 70%. Яка ймовірність того, що взята навмання деталь буде першого сорту?
Розв’язання
Позначимо події Н1 - деталь виготовлена на першому верстаті, Н2 – на другому, Н3 - на третьому. Подія А - деталь першого сорту.
Ймовірність - деталь першого сорту
Тобто за формулою повної ймовірності:
2.8 Знайти ймовірність того, що подія А відбудеться рівно 70 раз в 243 іспитах, якщо ймовірність появи цієї події в кожному іспиті = 0,25.
Розв’язання: За умовою, n =243, k = 70, р = 0,254; q=0,75. Так як n=243 – достатньо велике число, скористуємося локальною теоремою Лапласа.
див. Додаток 1, φ(1,37)=0,1561
маємо:
Відповідь: 0,0231
2.9 Ймовірність появи події в кожному із 100 незалежних іспитів дорівнює 0,8. Знайти ймовірність того, що подія відбувається не менше 75 разів і не більше 90 разів. Розв’язання: за інтегральною теоремою Лапласа
за умовою: n = 100; p =0.8; q = 0.2;
див. Додаток 2. Ф (-1,25) = -Ф(1,25)= - 0,3944 Ф(2,5) = 0,4938
Маємо Р
Відповідь: 0,8882 3 Запитання для самоконтролю 3.1 Дати означення ймовірності. 3.2 Назвіть, які події називаються несумісними і сумісними.
3.3 Визначте, що називається сумою двох подій та добутком. 3.4 Запишіть формулу повної ймовірності та формулу Байєса. 3.5 Запишіть формулу Бернуллі. 3.6 Запишіть локальну та інтегральну теореми Лапласа.
Індивідуальні завдання до самостійної роботи №2 Задача № 2 За формулою повної ймовірності та формулою Байєса, розв’язати задачу: На складі 12 + N деталей заводу №1, 20 + N деталей заводу №2, 18 + N деталей заводу №3. Ймовірність того, що деталь заводу №1 відмінної якості дорівнює 0,9, заводу № 2 дорівнює 0,6, заводу № 3 дорівнює 0,9. Знайти ймовірність того, що деталь навмання вибрана буде якісною і виготовлена на другому заводі. N – номер вашого варіанту.
Наприклад Ваш варіант №7,тоді деталей заводу №1 дорівнює 12+7=19, деталей заводу №2 дорівнює 20+7=27, деталей заводу №3 дорівнює 18+7=25.
Задача 3
За допомогою формули Бернулі розв’язати задачу. В лотереї з n білетів m мають виграти. Знайти ймовірність того, що серед навмання взятих k білетів 2 виграють.
Таблиця 1 Індивідуальні завдання до задачі №3
Задача №4 Користуючись локальною та інтегральною теоремами Лапласа, визначте ймовірність того, що із n посаджених дерев прийметься: 3.1 рівно m; 3.2 не менше k1 і не більше k2. Ймовірність того, що рослина прийметься на новому місці дорівнює Р.
Таблиця 2 Індивідуальні завдання до задачі №4
Теоретичні відомості 1.1 Означення. Випадковою називається величина, яка в результаті випробування приймає з деякою ймовірністю те чи інше значення, що залежить від результату випробування. Випадкові величини позначаються великими латинськими літерами: Х,У, Z, і т.д., а їх значення прописними літерами: х, у, z, і т.д.
Означення. Випадкова величина називається дискретною, якщо множина її значень скінчена, тобто множина значень утворює скінчену послідовність х1,х2,х3 …, хn. Означення. Відповідність між можливими значеннями х1,х2,х3 …, хn випадкової величини Х і їх ймовірностями р1,р2,р3 …, рn називається законом розподілення випадкової величини Х.
де р1 + р2 + … + рn = 1 Означення. Закон розподілення випадкової величини Х має вид.
і називається біномінальним законом розподілення.
1.2 Числові характеристики дискретних випадкових величин. Числа, які описують випадкову величину сумарно, такі числа називають числовими характеристиками випадкових величин. Такими характеристиками є: математичне сподівання або очікування, дисперсія, середнє квадратичне відхилення. Числові характеристики:
Математичне сподівання вказує на середнє значення випадкової величини
М(х)=
Дисперсія:
1.3 Означення. Функцією розподілу випадкової величини називають функцію F(x), яка визначає для кожного значення х ймовірність того, що випадкова величина Х приймає значення менше за х F(x)=P(X<x), 1.3.1
Властивості функції розподілу
0<F(x)<1, 1.3.2
F(x2)>F(x1),при х2>х1 1.3.3
1.4 Наслідок. Ймовірність того що випадкова величина Х приймае значення з інтервалом (а;b) дорівнює приросту функції розподілу на цьому інтервалі. P(a<X<b)=F(b)-F(a) 1.4.1
1.5 Означення. Щільністю розподілу ймовірностей неперервної випадкової величини називають першу похідну від функції розподілу.
f(x)=F'(x) 1.5.1
Нормальний закон розподілу Ймовірність того,що випадкова величина прийме значення, що належить інтервалу (α;β), обчислюється за формулою:
Де Ф(х)- функція Лапласа, дивись додаток 2 Ф(-х)=-Ф(х)
а – математичне сподівання, тобто середнє значення.
1.9 Ймовірність того, що абсолютна величина відхилення менше додатного числа ξ (епсілон), обчислюється за формулою:
Р(│х-а│<ξ)=2Ф( Розв’язування типових задач 2.1 Пристрій складається з трьох елементів, ймовірність відмови кожного елемента в одному іспиті дорівнює 0,1. Скласти закон розподілу числа елементів в одному іспиті. Розв'язання Дискретна випадкова величина Х має слідуючи можливі значення: Х1=0 (ні один з елементів пристрою не відмовив) Х2=1 (відмовив один елемент) Х3=2 (відмовили два елементи) Х4=3 (відмовили три елементи) Ймовірність відмови кожного елемента дорівнює 0,1, тоді q=1-0,1=0,9. За формулою Бернулі розрахуємо ймовірність всіх можливих випадків:
Запишемо біноміальний закон розподілу:
Таблиця 2.1.1 Біноміальний закон розподілу:
Контроль: 0,729+0,243+0,027+0,001=1 Знайдемо математичне сподівання:
Знайдемо дисперсію випадкової величини:
М(х2)= 02 0,729+12 0,243+22 0,027+32 0,001 = 0,243+4 0,027+9 0,001= 0,243+0,108+0,009=0,360
Д(х)=0,36-(0,4)2=0,36-0,16=0,2
Знайдемо середнє квадратичне відхилення:
Побудуємо полігон ймовірності:
Малюнок 1 Полігон ймовірності Задача 2.2 Знайти дисперсію випадкової величини Х, заданої функцією розподілу:
F(х)
Розв’язання
D(Х)
Знайдемо щільність розподілу
f(x)=
Знайдемо математичне очікування:
М(х)
Знайдемо дисперсію:
Відповідь: Задача 2.3
0, якщо х £ -1 F(х) = Ах +В, якщо –1 < х £ 3 1, якщо х > 3 2.3.1 Знайти параметри А і В 2.3.2 Накреслити графік у = F(х) 2.3.3 Визначити ймовірність, що випадкова величина Х Î [1;5] 2.3.4 Обчислити математичне сподівання і дисперсію заданої випадкової величини. Розв’язання: 2.3.1 Користуючись властивістю інтегральної функції:
Тоді
2.3.2 Графік F(x)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 Самостійна робота 1 (10 годин)
Самостійна робота 1 (10 годин)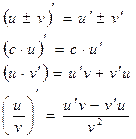
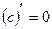 ,
, .
. ,
,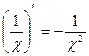 ,
, ,
, ,
, ,
,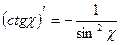 ,
,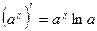 ,
,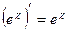 ,
, ,
, .
. на інтервалі (а; в) має похідну і зростає, то
на інтервалі (а; в) має похідну і зростає, то  >0 для будь-якого
>0 для будь-якого  є (а; в), а якщо спадає, то
є (а; в), а якщо спадає, то 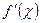 при переході через т.
при переході через т. 
 при
при  маємо
маємо  ,
,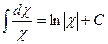 ,
, ,
, ,
, ,
, ,
, ,
,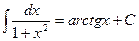 ,
,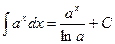 , а > 0, а ≠ 1,
, а > 0, а ≠ 1, ,
, .
. ,
, ,
,  ,
, 
 ;
;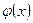 на зростання, спадання та точки екстремуму та побудувати графік функції;
на зростання, спадання та точки екстремуму та побудувати графік функції; ;
; 4.2
4.2  .
.



 ,
,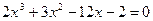 ,
,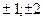 ,
, ,
, ,
, ,
,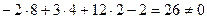 ,
, . А (
. А ( -
-  ).
).
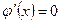

 маємо
маємо 



 > 0
> 0


 > 0
> 0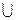

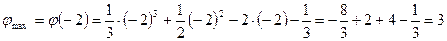 В (-2;3)- max
В (-2;3)- max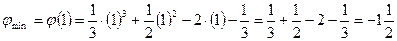 C (1;-1,5)- т. mіn
C (1;-1,5)- т. mіn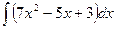 ;
;

 .
.

 ;
; на зростання, спадання та точки екстремуму та побудувати графік функції;
на зростання, спадання та точки екстремуму та побудувати графік функції;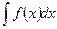 ;
; ,
, .
.



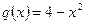

























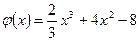






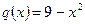













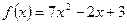

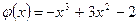

















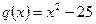







 ,
,

 ,
,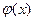 - дивись додаток №1
- дивись додаток №1
 ,
,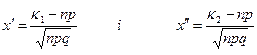
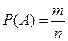
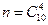 .
. , а групу стандартних деталей
, а групу стандартних деталей  , так як ці події виконуються одночасно, то наслідки які сприяють появі події А дорівнюють
, так як ці події виконуються одночасно, то наслідки які сприяють появі події А дорівнюють  .
.






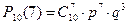



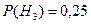
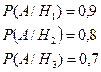

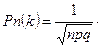 φ(х),
φ(х),

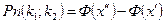 ,
, ;
;  ,
, ;
; 


 (75;90) = 0,4938+0,3944 = 0,8882
(75;90) = 0,4938+0,3944 = 0,8882




 , 1.2.1
, 1.2.1 , 1.2.2
, 1.2.2 якщо х є (а;в) 1.3.4
якщо х є (а;в) 1.3.4 1.8.1
1.8.1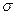 - середнє квадратичне відхилення,
- середнє квадратичне відхилення,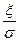 ) 1.9.2
) 1.9.2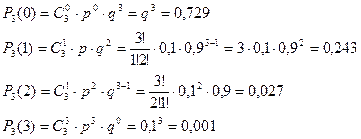
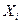
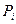
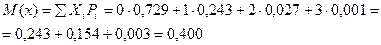
 2.1.1
2.1.1

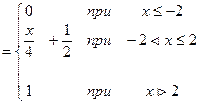


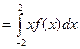 =
= 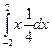 =
= 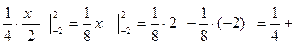
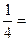
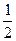

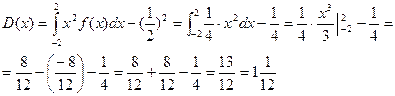
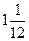
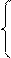 Задана інтегральна функція розподілу випадкової неперервної величини
Задана інтегральна функція розподілу випадкової неперервної величини ,
,