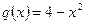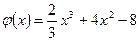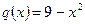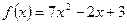Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Укладач: Рачицька Тетяна Федорівна - викладач методист Білгород – Дністровського державного морського рибопромислового технікумуСодержание книги
Поиск на нашем сайте
Методичні вказівки розглянуті та рекомендовані у навчальний процес цикловою комісією природничо-математичних дисциплін
Протокол № від ___ __________ 2011 року
Голова циклової комісії Лісогор Н.І.
ВСТУП
На вивчення даної дисципліни відводиться 81 година: з них 40 годин аудиторних і 41 година на самостійну роботу студентів. Мета та задача методичних вказівок до кожної роботи полягає в тому, щоб студент міг самостійно виконати індивідуальні завдання, користуючись вказівками та розв’язуванням типових задач і закріпити та вдосконалити свої знання набуті на лекціях. Навчитися самостійно працювати з додатковою літературою, робити висновки з самостійно розглянутих і вивчених розділів.
Оцінювання кожної роботи проводиться за п’ятибальною шкалою.. Якщо студент виконав менше 50% завдання, робота оцінюється на “2”; якщо від 50% до 75%, оцінка – “3”; якщо від 76% до 95%, оцінка – “4”; якщо більше 95%, оцінка – “5”. Самостійні роботи перевіряються після закінчення логічно-завершеної частини лекції та практичних робіт. Їх результати враховуються при виставленні підсумкової оцінки. Самостійні робота виконується в зошитах в клітинку на 24 аркушах. Перелік самостійних робіт
Самостійна робота №1 Елементи вищої математики – 10 години
Самостійна робота №2 Елементи теорії ймовірності – 10 годин Теми:. Класичне означення ймовірності. Теореми додавання і множення ймовірностей. Незалежні події. Формула повної ймовірності та формула Байєса. Формула Бернуллі. Локальна і інтегральна теорема Лапласа. Самостійна робота №3 Елементи теорії ймовірності - 11 годин Теми: Повторні події.. Випадкові величини. Дискретні випадкові величини та закон розподілу випадкової величини. Числові характеристики дискретної випадкової величини. Функція розподілу випадкової величини. Щільність розподілу. Числові характеристики неперервних випадкових величин. Нормальне розподілення, його числові характеристики.
Самостійна робота №4 Елементи математичної статистики – 10 годин Тема Варіаційний ряд. Статистичний ряд. Генеральна сукупність, вибірка. Полігон і гістограма. Статистичні та інтервальні оцінки параметрів розподілу генеральної сукупності.
Тема: Елементи вищої математики Мета: Повторення та удосконалення знань та вмінь набутих в курсі середньої школи з тем: “Похідна та її застосування”, “Визначений та невизначений інтеграл”. Теоретичне обґрунтування 1.1 Правила та формули диференціювання. Правила:
Формули:
1 2 3 4 5 6 7 8 9 10 11 12
1.2 Ознаки зростання та спадання функції. Екстремуми функції.
Теорема 1 Необхідна умова зростання. Якщо функція Теорема 2 Необхідна умова існування екстремуму. Якщо точка Теорема 3 Достатня умова існування екстремуму. Нехай функція 1 Якщо похідна 2 Якщо похідна
1.3 Таблиця інтегралів
1 2 3 4 5 6 7 8 9 10 11
Формула Ньютона – Лейбніца
де а – нижня границя; в – верхня границя; F(х) – первісна. Розв’язування типових задач Дано функції
Знайти: 1 2 дослідити функцію 3 обчислити невизначений інтеграл 4 обчислити визначений інтеграл: 4.1 5 обчислити площу фігури, обмеженої лініями Розв’язання
1
2 Дослідимо функцію на зростання, спадання та точки екстремуму 2.1 ОДЗ: х
2.2 Точки перетину з віссю ох: у = 0
х = 1, х = -1, х = 2, х = -2, серед цілих чисел коренів немає. Точки перетину з віссю оу: х = 0
2.3 Знайдемо похідну
2.4 Знайдемо критичні точки
За теоремою Вієта: 2.5 Розіб’ємо область визначення функції на інтервали і знайдемо знак похідної на кожному з них.
Висновок: функція зростає на функція спадає на в т.ч. х = – 2, існує max в т.ч. х = 1, існує min
2.6 Будуємо графік функції
Малюнок 1.1 Графік функції
3 Знайдемо
4 Обчислимо інтеграл
4.2
5 Знайдемо площу фігури, обмеженої лініями y=q(x) і віссю ox.
Малюнок 1.2 – Криволінійна трапеція, обмежена лініями
Питання для самоконтролю 3.1 Чому дорівнює похідна суми? 3.2 Чому дорівнює похідна дробу? 3.3 Чому дорівнює похідна добутку? 3.4 Ознаки зростання і спадання функції. Екстремум функції, 2 умови. 3.5 Як записується формула Ньютона – Лейбніца? 3.6 Геометричний зміст визначеного інтеграла. Індивідуальні завдання до самостійної роботи № 1 Знайти: 1 похідну 2 дослідити функцію 3 невизначений інтеграл 4 визначений інтеграл: 4.1 4.2 5 обчислити площу фігури, обмеженої лініями у=q(x) і віссю ох. Таблиця 1 Варіанти
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.160.250 (0.01 с.) |

 Самостійна робота 1 (10 годин)
Самостійна робота 1 (10 годин)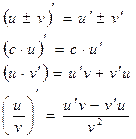
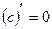 ,
, .
. ,
,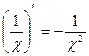 ,
, ,
, ,
, ,
,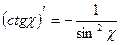 ,
,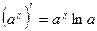 ,
,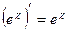 ,
, ,
, .
. на інтервалі (а; в) має похідну і зростає, то
на інтервалі (а; в) має похідну і зростає, то  >0 для будь-якого
>0 для будь-якого  є (а; в), а якщо спадає, то
є (а; в), а якщо спадає, то 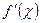 при переході через т.
при переході через т. 
 при
при  маємо
маємо  ,
,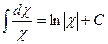 ,
, ,
, ,
, ,
, ,
, ,
,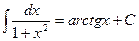 ,
,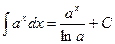 , а > 0, а ≠ 1,
, а > 0, а ≠ 1, ,
, .
. ,
, ,
,  ,
, 
 ;
;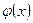 на зростання, спадання та точки екстремуму та побудувати графік функції;
на зростання, спадання та точки екстремуму та побудувати графік функції; ;
; 4.2
4.2  .
.



 ,
,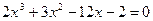 ,
,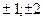 ,
, ,
, ,
, ,
,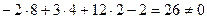 ,
, . А (
. А ( -
-  ).
).
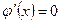

 маємо
маємо 



 > 0
> 0


 > 0
> 0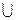

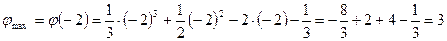 В (-2;3)- max
В (-2;3)- max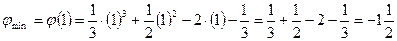 C (1;-1,5)- т. mіn
C (1;-1,5)- т. mіn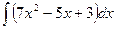 ;
;

 .
.

 ;
; на зростання, спадання та точки екстремуму та побудувати графік функції;
на зростання, спадання та точки екстремуму та побудувати графік функції;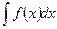 ;
; ,
, .
.