
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При прокатке в горизонтальных валкахСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В соответствии с уравнением Головина-Симса имеем
где h 1 – толщина полосы, выходящей из валков; S 0 – исходный раствор ненагруженных валков; Р – сила прокатки; Mк – модуль жесткости клети. Второй член уравнения (7.1) является упругой деформацией клети (валков, станины, нажимных винтов и гаек, подшипников, подушек и пр.). Сила прокатки зависит от многих переменных, основными из них являются P = f (h 0, h 1, b, s0, s1, sТ, R), (7.2) где h 0 и h 1 – толщина полосы до и после прокатки; b – ширина полосы; s0 и s1 – заднее и переднее удельные натяжения полосы; sТ – сопротивление деформации стали; R – радиус рабочих валков.) Функция (7.2) нелинейна. Линеаризацию её производят путем разложения в ряд Тейлора около начальных значений переменных, пренебрегая членами выше первого порядка. Приращения давления металла на валки приближенно округляют как полные дифференциалы
В качестве функции (7.2) выбирают известные зависимости для расчета силы прокатки. Продольную разнотолщинность полосы определяют как полный дифференциал уравнения (7.1)
В процессе прокатки рабочие нагрузки находятся в области линейного участка зависимости упругой деформации клети (см. рис.62). Пренебрегая изменением модуля упругости материала деталей клети в зависимости от колебания температуры и толщины масляной пленки в ПЖТ, второй член уравнения (7.4) не учитывают, и тогда
При подстановке уравнения (7.3) в уравнение (7.5) получаем основное уравнение продольной разнотолщинности полосы
По физическому смыслу коэффициенты у дифференциалов представляют собой передаточные коэффициенты, характеризующие влияние независимых переменных параметров процесса прокатки на разнотолщинность полосы. Выражение в скобках представляет собой изменение силы прокатки за счет непостоянства различных параметров прокатки, кроме выходящей толщины полосы. Поэтому уравнение (7.6) можно записать в виде
Углы наклона b1 и b2 упруго-пластичной кривой полосы являются модулем жесткости полосы М п, поэтому в окончательном виде основное уравнение продольной разнотолщинности имеет следующий вид
Совместное решение уравнения упругой деформации клети и кривой пластичности приведено на рис.64.
Точка 1 характеризует толщину полосы (h 1) после прокатки. При изменении свойств полосы (например, изменение температуры прокатки) и одной и той же исходной толщине толщина полосы изменится и станет h 2 > h 1. Изменится и сила прокатки Р 2 > Р 1 . Для того, чтобы получить ту же толщину полосы, что была в первом случае, необходимо изменить раствор валков с S 1 на S 2. При изменении модуля жесткости клети (например, применении гидрораспора) толщина полосы уменьшится, а сила прокатки увеличится Р 2 > Р 1 (рис.65). Если же необходимо будет прокатывать прежнюю толщину полосы h 1, то придется увеличивать раствор валков до S 2 (уменьшается «пружина» клети).
Представленные графические решения позволяют прогнозировать получающуюся толщину полосы, а если необходимо, то и значения величины изменения раствора валков. Можно использовать методику и для анализа колебаний толщины полосы в зависимости от параметров, входящих в уравнение (7.6). Например, для выявления степени влияния входной толщины на выходную толщину в каждой клети непрерывного стана, в уравнении (7.6) принимаем: D S =0; D b =0; Ds0=0; Ds1=0; DsТ=0; D R =0 и получаем
Полученные результаты удобно представить в виде графиков, один из которых показан на рис.66.
Из рисунка видно, что если в первую клеть чистовой группы входит полоса с разнотолщинностью 0,4 мм, то после первой клети её разнотолщинность будет примерно 0,2 мм, в седьмой же клети при h 0 = 0,4 мм имеем h 1 = 0,02 мм. С применением описанной методики определяют значения технологических передаточных коэффициентов для систем автоматики. Коэффициент выравнивания Влияние исходной разнотолщинности подката на конечную разнотолщинность полосы характеризует коэффициент выравнивания, определяемый как
где D h 0, D h 1 – продольная разнотолщинность подката и готовой полосы; h 0, h 1 –толщина подката и готовой полосы. Если K B > 1, то конечная относительная разнотолщинность полосы меньше начальной, и клеть или клети выравнивают полосу, если K B < 1, то наоборот. Чем больше клетей, тем в первом случае больше выравнивается полоса, во втором – увеличивается разнотолщинность. Для расчета коэффициента выравнивания предложена зависимость
где e – относительное обжатие, а На ШСГП и ТЛС K B > 1. Общий K B рассчитывают как K BS = K B1 × K B2 ×... × K Bn. Увеличение M к увеличивает K B.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.107 (0.006 с.) |

 , (7.1)
, (7.1) . (7.3)
. (7.3) . (7.4)
. (7.4) . (7.5)
. (7.5)
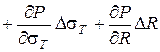 ). (7.6)
). (7.6) .
. . (7.7)
. (7.7)

 (при
(при  ).
).
 ,
, ,
, , то есть отношение частных производных от силы прокатки по входной и выходной толщине полосы.
, то есть отношение частных производных от силы прокатки по входной и выходной толщине полосы.


