Nondeterm minimax(position,position,mark)

%обчислення найкращого ходу і мінімаксної оцінки для певної позиції

nondeterm best(position_list,position,mark)

%вибір зі списку позицій-кандидатів найкращої позиції

% mark – оцінка найкращої позиції

Choice(position,mark,position,mark,position,mark)

% вибір або першої, або другої позиції

% залежно від ходу гравця чи противника

Clauses

Minimax(Pos,BestPos,O):-

turns(Pos, PosList),!, %PosList – список дозволених ходів

best(PosList, BestPos, O);

stat_o(Pos,O). %Pos не має продовжень

best([Pos],Pos,O):-

minimax(Pos,_,O),!.

best([Pos1|PosList],BestPos,BestO):-

minimax(Pos1,_,O1),

Best(PosList,Pos2,O2),

Choice(Pos1,O1,Pos2,O2,BestPos,BestO).

Choice(Pos0,O0,Pos1,O1,Pos0,O0):-

min_turn(Pos0), O0<O1,!;

max_turn(Pos0), O0>O1,!.

Choice(Pos0,O0,Pos1,O1,Pos1,O1).

turns(a, [b,c]).

turns(b, [d,e]).

turns(c, [f,g]).

turns(d, [h,i]).

turns(e, [j,k]).

turns(f, [l,m]).

turns(g, [n,o]).

max_turn(b).

max_turn(c).

max_turn(h).

max_turn(i).

max_turn(j).

max_turn(k).

max_turn(l).

max_turn(m).

max_turn(n).

max_turn(o)

min_turn(d).

min_turn(e).

min_turn(f).

min_turn(g).

stat_o(h,1).

stat_o(i,4).

stat_o(j,5).

stat_o(k,6).

stat_o(l,2).

stat_o(m,1).

stat_o(n,1).

stat_o(o,1).

Goal

Minimax(a, X, M).

 

Наведена програма на запит minimax(a, X, M), як і слід сподіватися, дає відповідь X=b, M=4, тобто найкращий хід із позиції а є a-b, а оцінка цього ходу і всієї позиції а – 4.

Основне відношення цієї програми –

minimax(Pos, BestPos, O),

де O – мінімаксна оцінка позиції Pos; BestPos – найкраща позиція-наступник позиції Pos (найкращий хід, який дозволяє досягнути оцінки О).

Відношення

Turns(Pos, PosList)

задає дозволені ходи гри: PosList – це список дозволених позицій-наступників позиції Pos. Передбачено, що ціль turns має неуспіх, якщо Pos є термінальною пошуковою позицією (листком дерева пошуку).

Відношення

Best(PosList, BestPos, O)

вибирає зі списку позицій-кандидатів PosList найкращу позицію BestPos. О – оцінка позиції BestPos і відповідно позиції Pos. Під найкращою оцінкою в цьому записі розуміють або максимальну, або мінімальну оцінку, залежно від того, з якого боку можливий хід.

 

Реалізація деяких методів пошуку в просторі станів

У мові Пролог

 

Простір станів у мові Пролог можна подати як відношення after(x, y). Наприклад, якщо простір станів можна зобразити у вигляді дерева, показаного на рис. 12, то його записують таким чином:

 

after(a,b).

after(b,c).

after(a,d).

After(d,e).

 

 

Рис. 12. Приклад дерева

 

 

Пошук углиб реалізований у мові Пролог за допомогою такої ідеї. Для того щоб знайти шлях Solution із певної вершини A в деяку цільову вершину, необхідно:

- якщо A – цільова вершина, то встановити Solution = A;

- якщо для вихідної вершини A існує вершина-наступник A1, така що можна провести шлях Solution1 із A1 у цільову вершину, то встановити Solution = [A | Solution1].

Мовою Пролог це правило записують так:

solve(A, [A]):-

Destination(A).

solve(A, [A|Solution]):-

After(A, A1),

Solve(A1, Solution).

 

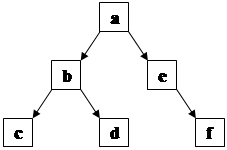
Ця програма має недолік – вона може зациклитися, якщо в просторі станів є цикли. Для її вдосконалення треба додати механізм виявлення циклів.

Пошук ушир програмувати більш складно, ніж пошук углиб, тому що доводиться зберігати всю множину вершин-кандидатів, а не тільки одну. Крім того, якщо нам треба знайти розв’язувальний шлях, то однієї множини вершин недостатньо. Тому будемо зберігати не множину вершин-кандидатів, а множину шляхів-кандидатів. Простір станів у цьому випадку зручно подавати за допомогою відношення children(x, [y, z]). Наприклад, для дерева, наведеного на рис. 13, можна записати таке:

 

children(a, [b, e]).

children(b, [c, d]).

children(e, [f]).

 

 

Рис. 13. Приклад дерева

 

Знайдемо відношення пошуку вшир breadth_star(Roads, Answer). Це відношення буде істинним, якщо існує шлях із множини кандидатів Roads, який можна продовжити до цільової вершини. Цей продовжений шлях і є Answer.

У розглядуваній реалізації множина шляхів-кандидатів буде подана як список шляхів, а кожен шлях – як список вершин, перерахованих у зворотному порядку, тобто головою списку буде остання з породжених вершин. Пошук починається з одноелементної множини кандидатів [[Start]].

Загальні принципи пошуку вшир такі. Для того щоб виконати пошук ушир за заданої множини шляхів-кандидатів, необхідно:

- якщо голова першого шляху – цільова вершина, то взяти цей шлях як розв’язок;

- у противному разі видалити перший шлях із множини кандидатів і створити множину всіх можливих продовжень цього шляху на один крок; множину продовжень додати в кінець множини шляхів-кандидатів, а потім виконати пошук ушир з отриманою новою множиною.

Подана нижче програма реалізує цей алгоритм.

breadth_first(Start,Answer):-

breadth_star([[Start]], Answer).

breadth_star([[H|Road]|_], [H|Road]):-

Destination(H).

breadth_star([[H|T]|Roads], Answer):-

children(H, Children), make_road(Children, [H|T], Child_Roads),

append1(Roads, Child_Roads, New_Roads),!,

breadth_star(New_Roads, Answer).

breadth_star(Roads, Answer). % випадок, якщо у Н немає наступника

 

Множину продовжень шляху породжують два відношення – children(H, Children) і make_road(Children, [H|T], Child_Roads), перше відношення спочатку породжує список вершин-наступників Children вершини H, а друге – список шляхів-спадкоємців Child_Roads, які ведуть із вершини H. Предикат make_road можна реалізувати так:

 

make_road([], _, []).

make_road([H|T], L, [New_L|T1]):-

append([H], L, New_L),

make_road(T, L,T1).

 

Предикат append1(Roads, Child_Roads, New_Roads) додає множину шляхів-продовжень у кінець множини шляхів-кандидатів:

 

append1([],L,L).

append1([X|L1],L2,[X|L3]):-

Append1(L1,L2,L3).

 

Якщо у вершини H немає вершин-наступників і відношення children(H, Children) неуспішне, відбувається альтернативний запуск процедури breadth_star(Roads, Answer).

Завдання 3

А. Розв’язати задачу про комівояжера, застосовуючи нижчевказані методи пошуку.

Б. Розв’язати задачу про туриста, застосовуючи зазначені нижче методи пошуку.

1. Метод перебору.

2. Метод пошуку в глиб.

3. Метод пошуку в шир.

4. Метод найкоротшого шляху.

5. Метод Мура.

6. Метод Дейкстри.

7. Метод гілок і меж.

8. Метод Нільсона.