Findall(ArgumentName, PredicateCall, ValuesList)

ArgumentName визначає, який параметр у вказаному предикаті PredicateCall слід зібрати в список ValuesList.

PredicateCall вказує предикат, із якого будуть зібрані значення.

ValuesList – вихіднийсписок значень, зібраних за допомогою бектрекінгу.

У поданій нижче програмі за допомогою предиката findall із БД збирають у список TownList1 назви всіх міст, а в список TownList2 – назви міст, до яких існує дорога з Києва:

 

Domains

town = symbol

town_list=town*

Facts

Town(town).

Predicates

Nondeterm road(town,town)

Clauses

Town(kyiv).

Town(lviv).

Town(dnipro).

Town(donetsk).

Road(kyiv,lviv).

Road(lviv,krakiv).

Road(kyiv,dnipro).

Road(dnipro,donetsk).

Goal

Findall(X, town(X), TownList1), write(TownList1), nl,

Findall(X, road(kyiv,X), TownList2), write(TownList2), nl.

 

Ігри

 

Ігри двох осіб із повною інформацією

 

Прикладами ігор із повною інформацією можуть бути шахи, шашки і под. У грі беруть участь два гравці, які роблять ходи по черзі, причому обидва вони мають повну інформацію про поточну ігрову ситуацію (на відміну від більшості карточних ігор). Гру вважають закінченою, якщо досягнуто позицію, яка згідно з правилами гри є термінальна (кінцева), наприклад матову позицію в шахах. Правила гри також визначають, який результат гри досягнуто в цій термінальній позиції.

Такі ігри можна подавати у вигляді дерева гри (або ігрового дерева). Вершини цього дерева відповідають ситуаціям, а дуги – ходам. Початкова ситуація гри – це коренева вершина; листки дерева – термінальні позиції.

У більшості ігор цього типу можливі такі результати: виграш, програш і нічия. Розглянемо ігри, які мають тільки два результати – виграш і програш. Ігри, у яких можлива нічия, можна спрощено вважати іграми з двома результатами – виграш і не-виграш. Двох учасників гри будемо називати гравцем і противником. Гравець може виграти в деякій нетермінальній позиції з ходом гравця (позиції гравця), якщо в ній існує який-небудь дозволений хід, який приводить до виграшу. Водночас деяка нетермінальна позиція з ходом противника (позиція противника) є виграна для гравця, якщо всі дозволені ходи з цієї позиції приводять до позицій, у яких можливий виграш. Ці правила повністю відповідають зображенню задач у вигляді І/АБО -дерева. Між поняттями, стосовними І/АБО -дерева, і поняттями, використовуваними в іграх, можна встановити взаємну відповідність таким чином.

Позиція гри – вершини, задачі.

Термінальні позиції виграшу – цільові вершини, тривіальні задачі.

Термінальні позиції програшу – задачі, які не мають розв'язку.

Виграні позиції – задачі, які мають розв'язок.

Позиції гравця – АБО -вершини.

Позиції противника – І -вершини.

Очевидно, що аналогічно поняття, стосовні пошуку в І/АБО -деревах, можна переосмислити в термінах пошуку в ігрових деревах.

Нижче наведено просту програму, яка визначає, чи є деяка позиція гравця виграна.

 

Database

Turn(symbol, symbol)

term_v(symbol)

term_p(symbol)

Predicates

Nondeterm vikt(symbol)

nondeterm turn_not_vikt(symbol, symbol)

Clauses

Vikt(P):-

term_v(P).

Vikt(P):-

not(term_p(P)),

Turn(P,P1),

not(term_p(P1)),

not(turn_not_vikt(P1,_)).

turn_not_vikt(P1,P2):-

Turn(P1,P2), not(vikt(P2)).

turn(a, b).

turn(a, c).

turn(b, d).

Turn(b, e).

Turn(c, f).

Turn(c, g).

term_v(d).

term_v(e).

term_p(f).

term_p(g).

Goal

vikt(a).

 

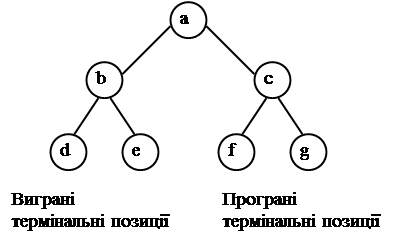
Програма перевіряє, чи виграна позиція а. У цьому випадку система дасть відповідь yes, тобто позиція а виграна (як видно з рис. 10, існують ходи з позиції а, які приводять до виграних термінальних позицій d та c). Якщо зробити запит щодо того, чи виграна позиція с, – vikt(c), система дасть відповідь no (не існує жодного ходу з позиції с, який приводить до виграшу).

 

Рис. 10. Просте дерево гри

 

У розглядуваному випадку правила гри вбудовані в предикат turn, який породжує всі дозволені ходи, а також у предикати term_v і term_p, що розпізнають термінальні позиції, які згідно з правилами гри є виграні або програні. Вираз not(term_p(P)) означає, що Р – нетермінальна позиція програшу, а вираз not(term_p(P1)) означає, що і наступна після Р позиція теж є нетермінальною позицією програшу. Вираз not(turn_not_vikt(P1,_)) говорить: не існує ходу противника, який приводить до невиграної позиції, іншими словами, усі ходи противника приводять до позицій, виграних із погляду гравця.

Так само як і аналогічна програма пошуку в І/АБО -графах, наведена вище програма застосовує стратегію пошуку вглиб. Крім того, у ній не виключена можливість зациклювання в одних і тих же позиціях. Намагання виправити цей недолік може призвести до ускладнень, оскільки правила деяких ігор допускають таке повторення позицій. Правда, дозвіл повторювати позиції часто має умовний характер, наприклад, за шаховими правилами після триразового повторення позиції може бути оголошена нічия.

Вищенаведена програма демонструє основні принципи програмування ігор. Але для практично прийнятної реалізації таких складних ігор, як шахи або го, потрібно застосовувати значно більш потужні методи. Надзвичайна комбінаторна складність таких ігор робить простий алгоритм, який проглядає дерево аж до термінальних ігрових позицій, абсолютно неприйнятним. Наприклад, якщо в кожній шаховій позиції існує приблизно 30 дозволених ходів і термінальні позиції розміщені на глибині 40 ходів, то простір пошуку шахової партії має астрономічні розміри – близько 10¹²⁰ позицій (один хід (два напівходи) – 30´30»1 000 позицій, 40 ходів – 1 000⁴⁰ позицій).

 

Мінімаксний принцип

 

Для ігор, які становлять інтерес, повний перегляд ігрового дерева неможливий, тому було розроблено інші методи, які передбачають перегляд тільки частини дерева гри. Серед цих методів існує стандартний метод пошуку, застосовуваний в ігрових програмах, в основі якого лежить мінімаксний принцип. Дерево гри проглядається тільки до деякої глибини (звичайно на декілька ходів), а потім для всіх кінцевих вершин дерева пошуку обчислюються оцінки за допомогою деякої оціночної функції. Ідея полягає в тому, щоб, отримавши оцінки цих термінальних пошукових вершин, не просуватися далі й таким чином зекономити час. Далі оцінки термінальних позицій поширюються вгору по дереву пошуку відповідно до мінімаксного принципу. У результаті всі вершини дерева пошуку одержують свої оцінки. І нарешті, ігрова програма, яка бере участь у деякій реальній грі, робить свій хід – хід, який приводить із вихідної (кореневої) позиції до найбільш перспективного (з погляду оцінки) її наступника.

Необхідно наголосити, що є різниця між деревом гри і деревом пошуку. Дерево пошуку – це тільки частина дерева гри (верхня частина), породжена в процесі пошуку. Таким чином, термінальні позиції пошуку зовсім не обов’язково повинні збігатися з термінальними позиціями самої гри.

Дуже багато залежить від оціночної функції, яка для більшості ігор, що становлять інтерес, є наближеною евристичною оцінкою шансів на виграш одного з учасників гри. Чим вища оцінка, тим більше в нього шансів виграти, і чим нижча оцінка, тим більше шансів на виграш у його противника. Оскільки один з учасників гри завжди прагне до високих оцінок, а інший – до низьких, дамо їм імена МАКС і МІН відповідно. МАКС завжди вибирає хід із максимальною оцінкою; на противагу йому МІН завжди вибирає хід із мінімальною оцінкою. Застосовуючи цей принцип (мінімаксний принцип) і знаючи значення оцінок для всіх вершин підніжжя дерева пошуку, можна визначити оцінки всіх інших вершин дерева. Із рис. 11 видно, що рівні позицій із ходом МАКС’а чергуються з рівнями позицій із ходом МІН’а. Оцінки вершин нижнього рівня визначають за допомогою оціночної функції. Оцінки всіх внутрішніх вершин можна визначити, рухаючись знизу вгору від рівня до рівня до досягнення кореневої вершини. Як видно з рис. 11, оцінка кореня дорівнює 4, і відповідно найкращий хід МАКС’а з позиції a –це a-b. Найкраща відповідь МІН’а на цей хід – b-d і т. д. Цю послідовність ходів називають також основним варіантом. Основний варіант показує, яка гра є мінімаксно-оптимальна для обох учасників. Необхідно наголосити, що оцінки всіх позицій, які входять до основного варіанта, збігаються. Виділені ходи утворюють основний варіант, тобто мінімаксно-оптимальну оцінку з обох сторін.

Рис. 11. Статичні (нижній рівень) і мінімаксні робочі оцінки вершин дерева пошуку

 

Розрізняють два види оцінок: оцінки вершин нижнього рівня й оцінки внутрішніх вершин (робочі оцінки). Перші з них називають також статичними, тому що їх обчислюють за допомогою статичної оціночної функції на відміну від робочих оцінок, одержуваних динамічно в процесі поширення статичних оцінок угору по дереву.

Правила поширення оцінок можна сформулювати таким чином. Будемо позначати статичну оцінку позиції P через v (P), а її робочу оцінку – через V (P). Нехай P ₁,…, P_n – дозволені наступники позиції P. Тоді співвідношення між статичними і робочими оцінками можна записати таким чином:

 

,

 

якщо P – термінальна позиція дерева пошуку (n =0);

 

,

 

якщо P – позиція з ходом МАКС’а;

 

,

 

якщо P – позиція з ходом МІН’а.

Нижче наведено програму, написану мовою Пролог, яка обчислює мінімаксну робочу оцінку для деякої заданої позиції (у розглядуваному випадку – позиції a для дерева гри, зображеного на рис. 11).

 

Domains

position = symbol

position_list = symbol*

mark = integer

Database - data

turns(position,position_list) %задання дозволених ходів гри

max_turn(position) %позиції, у яких робить ходи гравець

min_turn(position) %позиції, у яких робить ходи противник

stat_o(position,mark) %статичні оцінки для термінальних позицій

Predicates