Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие параллельной программыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон Амдаля. Любая параллельная программа содержит последовательную часть. Это ввод/вывод, менеджмент потоков, точки синхронизации и т.п. Обозначим долю последовательной части за
При неограниченном числе процессоров ускорение составит всего лишь
Так, например, если доля последовательной части 20%, то теоретически невозможно получить ускорение вычислений более чем в пять раз! Таким образом, превалирующую роль играет доля Еще пример. Возможно ли ускорение вычислений в два раза при переходе с однопроцессорной машины на четырехпроцессорную? Правильный ответ – не всегда, так как все зависит от доли
По графикам Более того, имея такую пессимистичную картину в теоретическом плане, на практике не избежать накладных расходов на поддержку многопоточных вычислений, состоящих из алгоритмических издержек (менеджмент потоков и т.п.), коммуникационных издержек на передачу информации между потоками и издержек в виде дисбаланса загрузки процессоров. Дисбаланс загрузки процессоров возникает, даже если удалось разбить исходную задачу на равные по сложности подзадачи, так как время их выполнения может существенно различаться по самым разным причинам (от конфликтов в конвейере до планировщика ОС). В точках синхронизации (хотя бы в точке завершения всей задачи) потоки вынуждены ожидать наиболее долго выполняемых, что приводит к простою значительной части процессоров. Закон Густавсона - Барсиса. Оптимистичный взгляд на закон Амдала дает закон Густафсона-Барсиса. Вместо вопроса об ускорении на n процессорах рассмотрим вопрос о замедлении вычислений при переходе на один процессор. Аналогично за
Теперь графики
Густафсон заметил, что, работая на многопроцессорных системах, пользователи склонны к изменению тактики решения задачи. Теперь снижение общего времени исполнения программы уступает объему решаемой задачи. Такое изменение цели обусловливает переход от закона Амдала к закону Густафсона. Например, на 100 процессорах программа выполняется 20 минут. При переходе на систему с 1000 процессорами можно достичь времени исполнения порядка двух минут. Однако для получения большей точности решения имеет смысл увеличить на порядок объем решаемой задачи (например, решить систему уравнений в частных производных на более тонкой сетке). Т.е. при сохранении общего времени исполнения пользователи стремятся получить более точный результат. Увеличение объема решаемой задачи приводит к увеличению доли параллельной части, так как последовательная часть (ввод/вывод, менеджмент потоков, точки синхронизации и т.п.) не изменяется. Таким образом, уменьшение доли f приводит к перспективным значениям ускорения. 15) Первая параллельная программа с использованием MPI. "Плавающий" вид получаемых результатов. Восстановление постоянство получаемых результатов. Общая схема MPI программ. Первая параллельная программа с использованием MPI
Для разделения фрагментов кода между процессами обычно используется подход, примененный в только что рассмотренной программе, – при помощи функции MPI_Comm_rank определяется ранг процесса, а затем в соответствии с рангом выделяются необходимые для процесса участки программного кода. Наличие в одной и той же программе фрагментов кода разных процессов также значительно усложняет понимание и, в целом, разработку MPI -программы. Как результат, можно рекомендовать при увеличении объема разрабатываемых программ выносить программный код разных процессов в отдельные программные модули (функции). Общая схема MPI -программы в этом случае будет иметь вид:
16) Определение времени выполнение MPI-программы. Возможная схема применения функции. Точность измерения времени Практически сразу же после разработки первых параллельных программ возникает необходимость определения времени выполнения вычислений для оценки достигаемого ускорения процессов решения задач за счет использования параллелизма. Используемые обычно средства для измерения времени работы программ зависят, как правило, от аппаратной платформы, операционной системы, алгоритмического языка и т.п. Стандарт MPI включает определение специальных функций для измерения времени, применение которых позволяет устранить зависимость от среды выполнения параллельных программ. Возможная схема применения функции MPI_Wtime может состоять в следующем:
10) MPI: основные понятия и определения. Понятие параллельной программы. Операции передачи данных Основу MPI составляют операции передачи сообщений. Среди предусмотренных в составе MPI функций различаются парные (point-to-point) операции между двумя процессами и коллективные (collective) коммуникационные действия для одновременного взаимодействия нескольких процессов. Понятие коммуникаторов Процессы параллельной программы объединяются в группы. Под коммуникатором в MPI понимается специально создаваемый служебный объект, объединяющий в своем составе группу процессов и ряд дополнительных параметров (контекст), используемых при выполнении операций передачи данных. Типы данных При выполнении операций передачи сообщений для указания передаваемых или получаемых данных в функциях MPI необходимо указывать тип пересылаемых данных. MPI содержит большой набор базовых типов данных, во многом совпадающих с типами данных в алгоритмических языках C и Fortran. Кроме того, в MPI имеются возможности для создания новых производных типов данных для более точного и краткого описания содержимого пересылаемых сообщений. Виртуальные топологии Парные операции передачи данных могут быть выполнены между любыми процессами одного и того же коммуникатора, а в коллективной операции принимают участие все процессы коммуникатора. В этом плане, логическая топология линий связи между процессами имеет структуру полного графа (независимо от наличия реальных физических каналов связи между процессорами). Вместе с этим, для изложения и последующего анализа ряда параллельных алгоритмов целесообразно логическое представление имеющейся коммуникационной сети в виде тех или иных топологий. В MPI имеется возможность представления множества процессов в виде решетки произвольной размерности. При этом, граничные процессы решеток могут быть объявлены соседними и, тем самым, на основе решеток могут быть определены структуры типа тор. Кроме того, в MPI имеются средства и для формирования логических (виртуальных) топологий любого требуемого типа.
Передача сообщений Для передачи сообщения процесс-отправитель должен выполнить функцию: int MPI_Send(void *buf, int count, MPI_Datatype type, int dest, int tag, MPI_Comm comm), где buf – адрес буфера памяти, в котором располагаются данные отправляемого сообщения, count – количество элементов данных в сообщении, type - тип элементов данных пересылаемого сообщения, dest - ранг процесса, которому отправляется сообщение, tag - значение-тег, используемое для идентификации сообщений, comm - коммуникатор, в рамках которого выполняется передача данных. Для указания типа пересылаемых данных в MPI имеется ряд базовых типов, полный список которых приведен дальше.MPI_Datatype - C Datatype; MPI_BYTE; MPI_CHAR - signed char; MPI_DOUBLE — double; MPI_FLOAT — float; MPI_INT — int; MPI_LONG — long; MPI_LONG_DOUBLE - long double; MPI_PACKED; MPI_SHORT — short; MPI_UNSIGNED_CHAR - unsigned char; MPI_UNSIGNED - unsigned int; MPI_UNSIGNED_LONG - unsigned long; MPI_UNSIGNED_SHORT - unsigned short. Отправляемое сообщение определяется через указание блока памяти (буфера), в котором это сообщение располагается. Используемая для указания буфера триада (buf, count, type) входит в состав параметров практически всех функций передачи данных, Процессы, между которыми выполняется передача данных, в обязательном порядке должны принадлежать коммуникатору, указываемому в функции MPI_Send, Параметр tag используется только при необходимости различения передаваемых сообщений, в противном случае в качестве значения параметра может быть использовано произвольное целое число (см. также описание функции MPI_Recv). Сразу же после завершения функции MPI_Send процесс-отправитель может начать повторно использовать буфер памяти, в котором располагалось отправляемое сообщение. Вместе с этим, следует понимать, что в момент завершения функции MPI_Send состояние самого пересылаемого сообщения может быть совершенно различным - сообщение может располагаться в процессе-отправителе, может находиться в процессе передачи, может храниться в процессе-получателе или же может быть принято процессом-получателем при помощи функции MPI_Recv. Тем самым, завершение функции MPI_Send означает лишь, что операция передачи начала выполняться и пересылка сообщения будет рано или поздно будет выполнена.
14) Прием сообщений (MPI_Recv). Для приема сообщения процесс-получатель должен выполнить функцию: int MPI_Recv(void *buf, int count, MPI_Datatype type, int source, int tag, MPI_Comm comm, MPI_Status *status), где buf, count, type – буфер памяти для приема сообщения, назначение каждого отдельного параметра соответствует описанию в MPI_Send, - source - ранг процесса, от которого должен быть выполнен прием сообщения, tag - тег сообщения, которое должно быть принято для процесса, comm - коммуникатор, в рамках которого выполняется передача данных, status – указатель на структуру данных с информацией о результате выполнения операции приема данных. Буфер памяти должен быть достаточным для приема сообщения, а тип элементов передаваемого и принимаемого сообщения должны совпадать; при нехватке памяти часть сообщения будет потеряна и в коде завершения функции будет зафиксирована ошибка переполнения, При необходимости приема сообщения от любого процесса-отправителя для параметра source может быть указано значение MPI_ANY_SOURCE, При необходимости приема сообщения с любым тегом для параметра tag может быть указано значение MPI_ANY_TAG, Параметр status позволяет определить ряд характеристик принятого сообщения: - status.MPI_SOURCE – ранг процесса-отправителя принятого сообщения, - status.MPI_TAG - тег принятого сообщения. Функция MPI_Get_count(MPI_Status *status, MPI_Datatype type, int *count) возвращает в переменной count количество элементов типа type в принятом сообщении. Вызов функции MPI_Recv не должен согласовываться со временем вызова соответствующей функции передачи сообщения MPI_Send – прием сообщения может быть инициирован до момента, в момент или после момента начала отправки сообщения. По завершении функции MPI_Recv в заданном буфере памяти будет располагаться принятое сообщение. Принципиальный момент здесь состоит в том, что функция MPI_Recv является блокирующей для процесса-получателя, т.е. его выполнение приостанавливается до завершения работы функции. Таким образом, если по каким-то причинам ожидаемое для приема сообщение будет отсутствовать, выполнение параллельной программы будет блокировано.
Режимы передачи данных Функция MPI_Send обеспечивает так называемый стандартный (Standard) режим отправки сообщений, при котором на время выполнения функции процесс-отправитель сообщения блокируется, после завершения функции буфер может быть использован повторно, состояние отправленного сообщения может быть различным - сообщение может располагаться в процессе-отправителе, может находиться в процессе передачи, может храниться в процессе-получателе или же может быть принято процессом-получателем при помощи функции MPI_Recv. Кроме стандартного режима в MPI предусматриваются следующие дополнительные режимы передачи сообщений: Синхронный (Synchronous) режим состоит в том, что завершение функции отправки сообщения происходит только при получении от процесса-получателя подтверждения о начале приема отправленного сообщения, отправленное сообщение или полностью принято процессом-получателем или находится в состоянии приема, Буферизованный (Buffered) режим предполагает использование дополнительных системных буферов для копирования в них отправляемых сообщений; как результат, функция отправки сообщения завершается сразу же после копирования сообщения в системный буфер, Режим передачи по готовности (Ready) может быть использован только, если операция приема сообщения уже инициирована. Буфер сообщения после завершения функции отправки сообщения может быть повторно использован. Для именования функций отправки сообщения для разных режимов выполнения в MPI используется название функции MPI_Send, к которому как префикс добавляется начальный символ названия соответствующего режима работы, т.е. MPI_Ssend – функция отправки сообщения в синхронном режиме, MPI_Bsend – функция отправки сообщения в буферизованном режиме, MPI_Rsend – функция отправки сообщения в режиме по готовности. Список параметров всех перечисленных функций совпадает с составом параметров функции MPI_Send. Для использования буферизованного режима передачи должен быть создан и передан MPI буфер памяти для буферизации сообщений – используемая для этого функция имеет вид int MPI_Buffer_attach(void *buf, int size), где buf - буфер памяти для буферизации сообщений, size – размер буфера. После завершения работы с буфером он должен быть отключен от MPI при помощи функции: int MPI_Buffer_detach(void *buf, int *size). По практическому использованию режимов можно привести следующие рекомендации: Режим передачи по готовности формально является наиболее быстрым, но используется достаточно редко, т.к. обычно сложно гарантировать готовность операции приема, Стандартный и буферизованный режимы также выполняются достаточно быстро, но могут приводить к большим расходам ресурсов (памяти) – в целом может быть рекомендован для передачи коротких сообщений, Синхронный режим является наиболее медленным, т.к. требует подтверждения приема. В тоже время, этот режим наиболее надежен – можно рекомендовать его для передачи длинных сообщений.
Синхронизация вычислений В ряде ситуаций независимо выполняемые в процессах вычисления необходимо синхронизировать. Так, например, для измерения времени начала работы параллельной программы необходимо, чтобы для всех процессов одновременно были завершены все подготовительные действия, перед окончанием работы программы все процессы должны завершить свои вычисления и т.п.
int MPI_Barrier(MPI_Comm comm), где
27) Под производным типом данных в MPI можно понимать описание набора значений предусмотренного в MPI типа, причем в общем случае описываемые значения не обязательно непрерывно располагаются в памяти. Задание типа в MPI принято осуществлять при помощи карты типа (type map) в виде последовательности описаний входящих в тип значений, каждое отдельное значение описывается указанием типа и смещения адреса месторасположения от некоторого базового адреса, т.е. Часть карты типа с указанием только типов значений именуется в MPI сигнатурой типа. Сигнатура типа описывает, какие базовые типы данных образуют некоторый производный тип данных MPI и, тем самым, управляет интерпретацией элементов данных при передаче или получении сообщений. Смещения карты типа определяют, где находятся значения данных. Поясним рассмотренные понятия на следующем примере. Пусть в сообщение должны входить значения переменных: double a; /* адрес 24 */ double b; /* адрес 40 */ int n; /* адрес 48 */Тогда производный тип для описания таких данных должен иметь карту типа следующего вида:{(MPI_DOUBLE,0),(MPI_DOUBLE,16),(MPI_INT,24)}. Дополнительно для производных типов данных в MPI используется следующий ряд новых понятий: Нижняя граница типа, верхняя граница типа, протяженность типа. Согласно определению нижняя граница есть смещение для первого байта значений рассматриваемого типа данных. Соответственно верхняя граница представляет собой смещение для байта, располагающегося вслед за последним элементом рассматриваемого типа данных. При этом величина смещения для верхней границы может быть округлена вверх с учетом требований выравнивания адресов. Следует также указать на различие понятий протяженности и размера типа. Протяженность – это размер памяти в байтах, который нужно отводить для одного элемента производного типа. Размер типа данных - это число байтов, которые занимают данные (разность между адресами последнего и первого байтов данных).. Для получения значения протяженности и размера типа в MPI предусмотрены функции: int MPI_Type_extent(MPI_Datatype type, MPI_Aint *extent), int MPI_Type_size (MPI_Datatype type, MPI_Aint *size). Определение нижней и верхней границ типа может быть выполнено при помощи функций: int MPI_Type_lb (MPI_Datatype type, MPI_Aint *disp),int MPI_Type_ub(MPI_Datatype type, MPI_Aint *disp).Важной и необходимой при конструировании производных типов является функция получения адреса переменной: int MPI_Address (void *location, MPI_Aint *address) Для снижения сложности в MPI предусмотрено несколько различных способов конструирования роизводных типов: Непрерывный способ позволяет определить непрерывный набор элементов существующего типа как новый производный тип. Векторный способ обеспечивает создание нового производного типа как набора элементов существующего типа, между элементами которого существуют регулярные промежутки по памяти. При этом,размер промежутков задается в числе элементов исходного типа, в то время, как в варианте H-векторного способа этот размер указывается в байтах. Индексный способ отличается от векторного метода тем, что промежутки между элементами исходного типа могут иметь нерегулярный характер. Структурный способ обеспечивает самое общее описание производного типа через явное указание карты создаваемого типа данных. При непрерывном способе конструирования производного типа данных в MPI используется функция: int MPI_Type_contiguous(int count,MPI_Data_type oldtype,MPI_Datatype *newtype). При векторном способе конструирования производного типа данных в MPI используются функции: - int MPI_Type_vector (int count, int blocklen, int stride, MPI_Data_type oldtype, MPI_Datatype *newtype), где count – количество блоков, blocklen – размер каждого блока, stride – количество элементов, расположенных между двумя соседними блоками oldtype - исходный тип данных, newtype - новый определяемый тип данных.-int MPI_Type_hvector (int count, int blocklen, MPI_Aint stride,MPI_Data_type oldtype, MPI_Datatype *newtype)При индексном способе конструирования производного типа данных в MPI используются функции:MPI_Type_indexed, MPI_Type_hindexedКак отмечалось ранее, структурный способ является самым общим методом конструирования производного типа данных при явном задании соответствующей карты типа. Использование такого способа производится при помощи функции: MPI_Type_struct,
29) При индексном способе конструирования производного типа данных в MPI используются функции: int MPI_Type_indexed (int count, int blocklens[], int indices[], MPI_Data_type oldtype, MPI_Datatype *newtype), где - count – количество блоков, - blocklens – количество элементов в каждов блоке, - indices – смещение каждого блока от начала типа (в количестве элементов исходного типа), - oldtype - исходный тип данных, - newtype - новый определяемый тип данных. int MPI_Type_hindexed (int count, int blocklens[], MPI_Aint indices[], MPI_Data_type oldtype, MPI_Datatype *newtype). Как следует из описания, при индексном способе новый производный тип создается как набор блоков разного размера из элементов исходного типа, при этом между блоками могут иметься разные промежутки по памяти. Для пояснения данного способа можно привести пример конструирования типа для описания верхней треугольной матрицы размером nxn: // конструирование типа для описания верхней треугольной матрицы for (i=0, i<n; i++) { blocklens[i] = n - i; indices[i] = i * n + i; } MPI_Type_indexed (n, blocklens, indices, &UTMatrixType, &ElemType).Как и ранее, способ конструирования, определяемый функцией MPI_Type_hindexed, отличается тем, что элементы indices для определения интервалов между блоками задаются в байтах, а не в элементах исходного типа данных. Следует отметить, что существует еще одна дополнительная функция MPI_Type_create_indexed_block индексного способа конструирования для определения типов с блоками одинакового размера (данная функция предусматривается стандартом MPI-2). Постановка задачи В результате умножения матрицы А размерности [n,m] и вектора b, состоящего из n элементов, получается вектор c размера m, каждый i-ый элемент которого есть результат скалярного умножения i-й строки матрицы А(обозначим эту строчку ai) и вектора b
Тем самым получение результирующего вектора c предполагает повторение m однотипных операций по умножению строк матрицы A и вектора b. Каждая такая операция включает умножение элементов строки матрицы и вектора b (n операций) и последующее суммирование полученных произведений(n-1 операций). Общее количество необходимых скалярных операций есть величина Последовательный алгоритм умножения матрицы на вектор может быть представлен следующим образом. Исходные данные: A[m][n]– матрицы размерности [n,m]. b[n]– вектор, состоящий из n элементов. Результат: c[n] – вектор изm элементов. Поcледовательный алгоритм умножения матрицы на вектор for (i = 0; i < m; i++) { c[i] = 0; for (j = 0; j < n; j++){ c[i] += A[i][j]*b[j];} } Матрично-векторное умножение - это последовательность вычисления скалярных произведений. Поскольку каждое вычисление скалярного произведения векторов длины n требует выполнения n операций умножения и n-1 операций сложения, его трудоемкость порядка O(n). Для выполнения матрично-векторного умножения необходимо выполнить m операций вычисления скалярного произведения, таким образом, алгоритм имеет трудоемкость порядка O(mn). Анализ эффективности Для анализа эффективности параллельных вычислений здесь и далее будут строиться два типа оценок. В первой из них трудоемкость алгоритмов оценивается в количестве вычислительных операций, необходимых для решения поставленной задачи, без учета затрат времени на передачу данных между процессорами, а длительность всех вычислительных операций считается одинаковой. Кроме того, константы в получаемых соотношениях, как правило, не указываются- для первого типа оценок важен прежде всего порядок сложности алгоритма, а не точное выражение времени выполнения вычислений. Как результат, в большинстве случаев подобные оценки получаются достаточно простыми и могут быть использованы для начального анализа эффективности разрабатываемых алгоритмов и методов. Второй тип оценок направлен на формирование как можно более точных соотношений для предсказания времени выполнения алгоритмов. Получение таких оценок проводится, как правило, при помощи уточнения выражений, полученных на первом этапе. Для этого в имеющиеся соотношения вводятся параметры, задающие длительность выполнения операций, строятся оценки трудоемкости коммуникационных операций, указываются все необходимые константы. Точность получаемых выражений проверяется при помощи проведения вычислительных экспериментов, по результатам которых времена выполненных расчетов сравниваются с теоретически предсказанными оценками длительностей вычислений. Как результат, оценки подобного типа имеют, как правило, более сложный вид, но позволяют более точно оценивать эффективность разрабатываемых методов параллельных вычислений. Рассмотрим трудоемкость алгоритма умножения матрицы на вектор. В случае, если матрица А квадратная(m=n), последовательный алгоритм умножения матрицы на вектор имеет сложность С учетом этой оценки показатели ускорения и эффективности параллельного алгоритма имеют вид:
Построенные выше оценки времени вычислений выражены в количестве операций и, кроме того, определены без учета затрат на выполнение операций передачи данных. Используем ранее высказанные предположения о том, что выполняемые операции умножения и сложения имеют одинаковую длительность τ. Кроме того, будем предполагать также, что вычислительная система является однородной, т.е. все процессоры, составляющие эту систему, обладают одинаковой производительностью. С учетом введенных предположений время выполнения параллельного алгоритма, связанное непосредственно с вычислениями, составляет
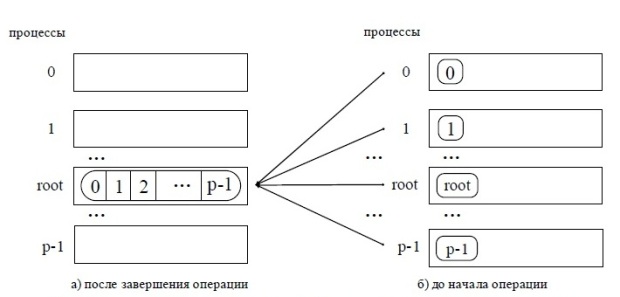
25. Обобщенная передача данных от всех процессов одному процессу. Операция обобщенной передачи данных от всех процессоров одному процессу (сбор данных) является обратной к процедуре распределения данных (см. рис. 5.5). Для выполнения этой операции в MPI предназначена функция: int MPI_Gather(void *sbuf,int scount,MPI_Datatype stype,void *rbuf,int rcount,MPI_Datatype rtype,int root, MPI_Comm comm), где sbuf, scount, stype - параметры передаваемого сообщения, rbuf, rcount, rtype - параметры принимаемого сообщения, root – ранг процесса, выполняющего сбор данных, comm - коммуникатор, в рамках которого выполняется передача данных.
int MPI_Allgather(void *sbuf, int scount, MPI_Datatype stype, void *rbuf, int rcount, MPI_Datatype rtype, MPI_Comm comm). Выполнение общего варианта операции сбора данных, когда размеры передаваемых процессами сообщений могут быть различны, обеспечивается при помощи функций MPI_Gatherv и MPI_Allgatherv. Пример использования функции MPI_Gather рассматривается в разделе 7 при разработке параллельных программ умножения матрицы на вектор.
Закон Амдаля. Любая параллельная программа содержит последовательную часть. Это ввод/вывод, менеджмент потоков, точки синхронизации и т.п. Обозначим долю последовательной части за
При неограниченном числе процессоров ускорение составит всего лишь
Так, например, если доля последовательной части 20%, то теоретически невозможно получить ускорение вычислений более чем в пять раз! Таким образом, превалирующую роль играет доля Еще пример. Возможно ли ускорение вычислений в два раза при переходе с однопроцессорной машины на четырехпроцессорную? Правильный ответ – не всегда, так как все зависит от доли
По графикам Более того, имея такую пессимистичную картину в теоретическом плане, на практике не избежать накладных расходов на поддержку многопоточных вычислений, состоящих из алгоритмических издержек (менеджмент потоков и т.п.), коммуникационных издержек на передачу информации между потоками и издержек в виде дисбаланса загрузки процессоров. Дисбаланс загрузки процессоров возникает, даже если удалось разбить исходную задачу на равные по сложности подзадачи, так как время их выполнения может существенно различаться по самым разным причинам (от конфликтов в конвейере до планировщика ОС). В точках синхронизации (хотя бы в точке завершения всей задачи) потоки вынуждены ожидать наиболее долго выполняемых, что приводит к простою значительной части процессоров. Закон Густавсона - Барсиса. Оптимистичный взгляд на закон Амдала дает закон Густафсона-Барсиса. Вместо вопроса об ускорении на n процессорах рассмотрим вопрос о замедлении вычислений при переходе на один процессор. Аналогично за
Теперь графики
Густафсон заметил, что, работая на многопроцессорных системах, пользователи склонн
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.018 с.) |

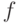 . Тогда доля параллельной части будет
. Тогда доля параллельной части будет 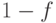 . В 1967 году Амдал рассмотрел ускорение такой программы на
. В 1967 году Амдал рассмотрел ускорение такой программы на 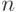 процессорах, исходя из предположения линейного ускорения параллельной части:
процессорах, исходя из предположения линейного ускорения параллельной части:
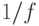 .
.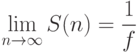
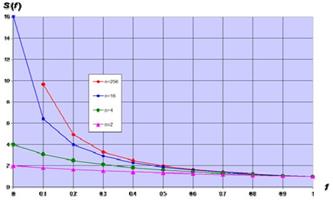
 можно увидеть, что при
можно увидеть, что при 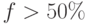 ни о каком существенном ускорении говорить не приходится. Только если доля
ни о каком существенном ускорении говорить не приходится. Только если доля 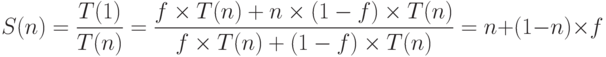

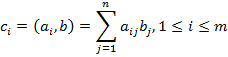
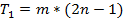
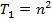 . В случае параллельных вычислений каждый процессор производит умножение только части(полосы) матрицы A на вектор b, размер этих полос равен n/p строк. При вычислении скалярного произведения одной строки матрицы и вектора необходимо произвести n операций умножения и (n-1) операций сложения. Следовательно, вычислительная трудоемкость параллельного алгоритма определяется выражением:
. В случае параллельных вычислений каждый процессор производит умножение только части(полосы) матрицы A на вектор b, размер этих полос равен n/p строк. При вычислении скалярного произведения одной строки матрицы и вектора необходимо произвести n операций умножения и (n-1) операций сложения. Следовательно, вычислительная трудоемкость параллельного алгоритма определяется выражением: 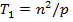
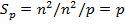 ;
;