
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод : сечение в точке в бруса расположено неподвижно в заделке, также, как и сечение в точке а, оно не может смещаться и его перемещение равно нулю.Содержание книги
Поиск на нашем сайте
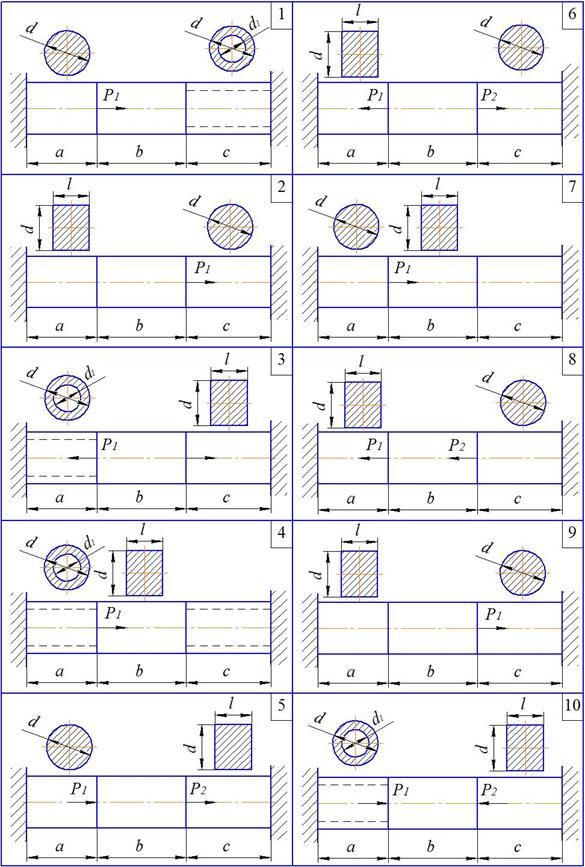
Задание №3 для курсового проектирования «Статически неопределимая задача деформации растяжения-сжатия» Для бруса (рис.3.18), имеющего различные площади поперечных сечений участков и находящегося под действием продольных сил, используя метод сечений, построить эпюру нормальных сил N(y). Из условия прочности определить размеры поперечных сечений. Построить эпюры нормальных напряжений σ(y) и абсолютных деформаций отдельных участков бруса Δℓ(y). Провести анализ напряженного состояния для опасных сечений. Принять материал стержня – сталь с допускаемым напряжением [σ]=140 МПа и модулем продольной упругости Е=2·105 МПа.
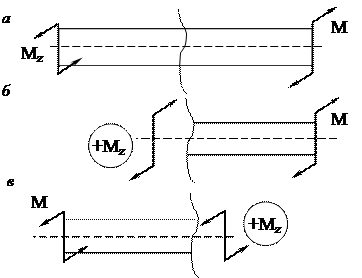
Рис.3.18. Расчетные схемы балок переменного сечения при деформации растяжения-сжатия Деформация кручения вала Правило знаков при построении эпюр крутящих моментов Вал нагружен внешними крутящими моментами M(рис. 3.19 а). Если рассечь вал и заменить отсеченную часть внутренним крутящим моментом MZ, то крутящий момент MZ считаем положительным, если его вращение происходит против часовой стрелки, если смотреть на него со стороны внешней нормали к сечению (рис.3.19 б – при рассмотрении правой части, рис. 3.19 в – при рассмотрении левой части). Для построения эпюры внутренних крутящих моментов MZ необходимо составить уравнение равновесия отсеченной части вала.
Рис. 3.19. Правило знаков внутренних крутящих моментов MZ при деформации кручения: а – схема нагружения вала; б – при рассмотрении правой части вала; в – при рассмотрении левой части вала
Условие прочности при кручении вала с круглым поперечным сечением:
где Для круглого поперечного сечения: Для кольцевого поперечного сечения: Условие прочности при кручении вала с прямоугольным поперечным сечением:
где а – большая сторона прямоугольника; b – малая сторона прямоуголь-ника; α – коэффициент, который зависит от отношения сторон а/ b. Угол поворота поперечного сечения стержня φ =φ0+ где φ0 – угол поворота левого торцевого сечения в начале координат, G ⋅ Если Если сечение прямоугольное, то формула принимает вид φ = φ 0 + где β – коэффициент, который зависит от отношения сторон а/ b. Числовые значения коэффициентов α и β приведены в таблице 3.1.
Таблица 3.1. Значения коэффициентов α, β, γ
Пример 5. Деформация кручения вала Для стального вала постоянного поперечного сечения, нагруженного внешними крутящими моментами (рис. 3.20 а), требуется, используя метод сечений, построить эпюру внутренних крутящих моментов MZ, из условия прочности подобрать размеры круглого, кольцевого и прямоугольного поперечных сечений, если [τ] = 80 МПа, D/d = 1,5. В опасном сечении построить эпюры касательных напряжений τ и сравнить массы валов. Дано: ℓ1 = 1 м; ℓ2 = 1,8 м; ℓ3 = 1,2 м; М = 20 кН·м; [τ] = 80 МПа; D/d = 1,5; a / b = 2; G = 0,8·105 МПа. Решение: 1. Определение опорного момента в заделке А Уравнение равновесия вращающих моментов, относительно оси Откуда 2. Определение внутренних вращающих моментов Стержень имеет три участка, границами которых служат сечения, где приложены внешние моменты В результате получаем уравнения равновесия: Участок АВ (
Участок ВС (
Участок CD (
Откуда
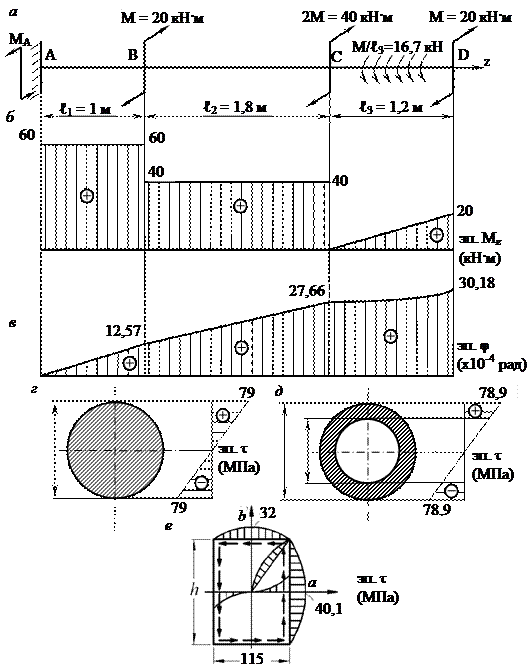
Вращающие моменты на каждом из участков известны, что позволяет легко построить эпюру вращающих моментов (см. рис. 3.20 б). Максимальный вращающий момент
Рис. 3.20. Пример расчета вала постоянного поперечного сечения, нагруженного внешними крутящими моментами М: а – расчетная схема нагружения; б – эпюра внутренних крутящих моментов MZ по длине z вала; в – эпюра угловых перемещений поперечных сечений вала φ (z); г – эпюра касательных напряжений вала круглого поперечного сечения; д – эпюра касательных напряжений вала кольцевого поперечного сечения; е – эпюра касательных напряжений вала прямоугольного поперечного сечения
Рис. 3.21. Метод сечений для определения крутящих моментов МZ: а – расчетная схема вала; б – определение МZ1 ; в – определение МZ2; г – определение МZ3
3. Подбор сечения вала из условия прочности Условие прочности для вала круглого поперечного сечения имеет вид:
откуда полярный момент сопротивления сечения:
Определяем размеры круглого поперечного сечения
Принимаем d = 157 мм.
Определяем размеры кольцевого поперечного сечения
Принимаем D = 169 мм; d = D/1,5 = 169/1,5 = 113 мм. Условие прочности для вала прямоугольного поперечного сечения имеет вид: откуда с учетом, что а = 2 b, получаем
Принимаем b = 115 мм; а = 2 b = 2·115 = 230 мм. 4. Построение эпюры угловых перемещений для вала круглого поперечного сечения (d = 157 мм) Угловые перемещения сечений определяются по формуле
где Jp - полярный момент инерции
GJp – крутильная жесткость вала
Определяем угловые перемещения сечений, начиная с неподвижного закрепленного конца. Сечение А расположено в заделке, оно не может поворачиваться и его угловое перемещение равно 0.
Сечение В: Сечение С: Сечение D:
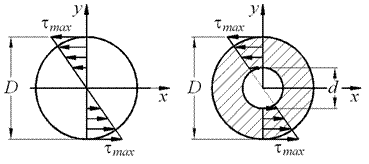
5. Построение эпюр касательных напряжений Для круглого поперечного сечения:
Эпюра касательных напряжений вала круглого поперечного сечения приведена на рисунке 3.20 г. Для кольцевого поперечного сечения:
Напряжения на внутреннем кольце сечения:
Эпюра касательных напряжений вала кольцевого поперечного сечения приведена на рисунке 3.20 д. Для прямоугольного поперечногое сечения:
Эпюра касательных напряжений вала прямоугольного поперечного сечения приведена на рисунке 3.20 е. 6. Сравнение масс валов различных поперечных сечений Массы валов круглого и кольцевого сечений относятся как площади их поперечных сечений. Площадь круглого сечения – Площадь кольцевого сечения –
Площадь прямоугольного сечения – Fпр = a ⋅ b.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.252.194 (0.008 с.) |

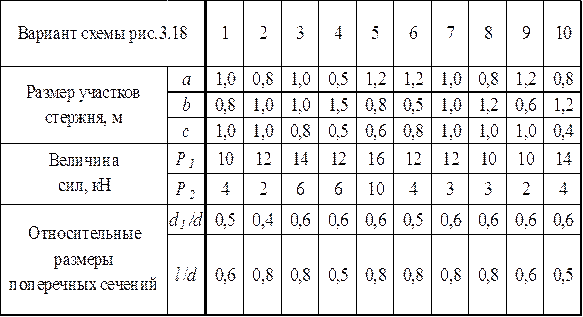
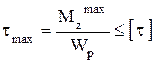 ,
,
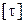 – допускаемое касательное напряжение;
– допускаемое касательное напряжение; 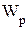 – полярный момент сопротивления сечения.
– полярный момент сопротивления сечения.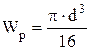 .
.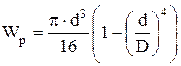 .
.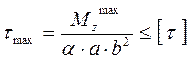 ,
,

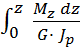 ,
,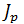 – жесткость при кручении; G – модуль сдвига Кулона;
– жесткость при кручении; G – модуль сдвига Кулона; 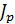 – полярный момент инерции сечения.
– полярный момент инерции сечения.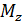 = const , то φ = φ 0 +
= const , то φ = φ 0 + 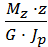 .
.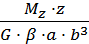 .
.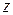 , имеет вид:
, имеет вид: 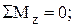
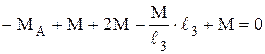
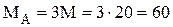 кН·м.
кН·м. методом сечений и построение эпюры
методом сечений и построение эпюры 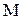 . Для обнаружения вращающих моментов на этих участках используем метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях
. Для обнаружения вращающих моментов на этих участках используем метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях 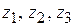 и рассматриваем равновесие одной из частей рассеченного стержня, заменяя действие отброшенных частей внутренними вращающими моментами
и рассматриваем равновесие одной из частей рассеченного стержня, заменяя действие отброшенных частей внутренними вращающими моментами 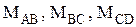 (рис. 3.21 а).
(рис. 3.21 а).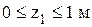 ) – рис. 3.21 б:
) – рис. 3.21 б: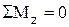 ;
; 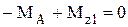 . Откуда
. Откуда 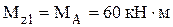
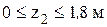 ) – рис. 3.21 в:
) – рис. 3.21 в: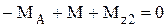 . Откуда
. Откуда 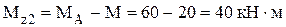
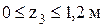 ) – рис. 3.21 г:
) – рис. 3.21 г: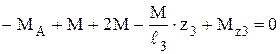 .
.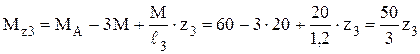 .
.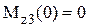 .
. 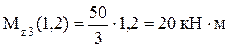 .
.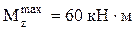 .
.



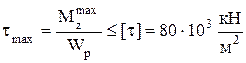 ,
,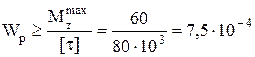 м3.
м3.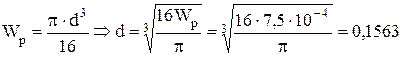 м.
м.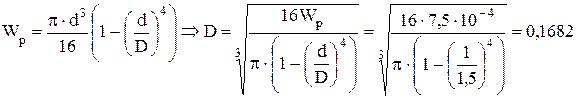 м.
м.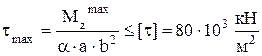 ,
,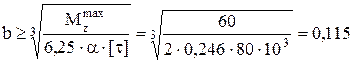 м.
м.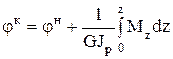 ,
,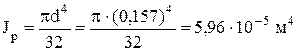 .
.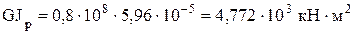 .
.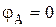 .
.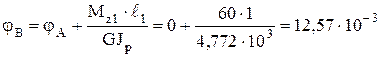 рад.
рад.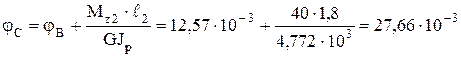 рад.
рад.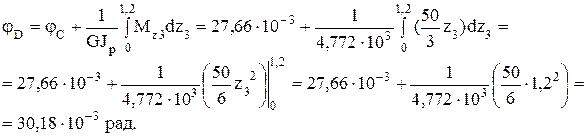
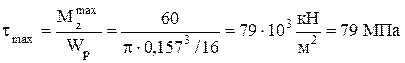 .
.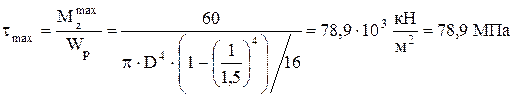 .
.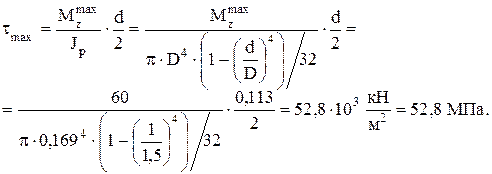
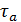 =
= 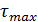 =
= 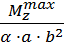 =
= 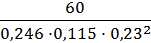 = 40,1⋅
= 40,1⋅ 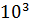
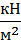 = 40,1 МПа,
= 40,1 МПа,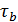 = γ ⋅
= γ ⋅  .
.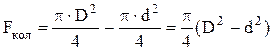 .
.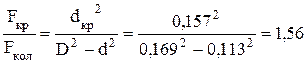 .
.


