
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимая задача
Деформации растяжения-сжатия Статически неопределимыми называются задачи, которые нельзя решить с помощью только уравнений статики. Дополнительные уравнения составляются из рассмотрения деформаций системы. Назовем степенью статической неопределенности n разность между числом неизвестных R и числом независимых уравнений статики У, которые можно составить для данной задачи: n = R – У. (3.19) На рис. 3.13 показано различие между статически определимыми и статически неопределимыми системами.
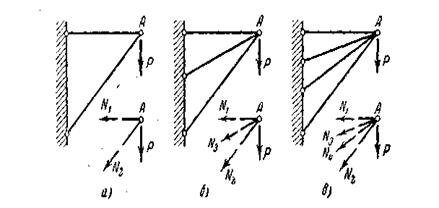
Рис. 3.13. Виды задач при растяжении-сжатии: а – статически определимая задача; б –один раз статически неопределимая задача (n = 3 – 2= 1); в – два раза статически неопределимая задача (n = 4 – 2= 2)
Покажем другие типичные статически неопределимые системы (рис. 3.14, 3.15).
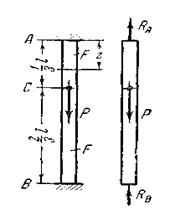
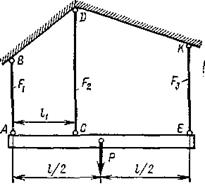
Рис. 3.14. «Лишняя» опора Рис. 3.15. «Лишний» подвес На данные системы наложено по одной «лишней» связи, то есть они являются один раз статически неопределимыми. Свойства статически неопределимых систем 1.Статически неопределимые системы являются более надежными конструкциями, т.к. сохраняют геометрическую неизменяемость после удаления (разрушения) «лишних» связей, а в статически определимых системах потеря хотя бы одной связи неизбежно ведет к геометрической изменяемости системы, следовательно, к неспособности нести нагрузку. 2.Статически неопределимые системы более жесткие, чем аналогичные статически определимые, т.к при одной и той же внешней нагрузке перемещения и деформации, а, следовательно, и внутренние усилия в них меньше. 3.Изменение температуры конструкции и деформация опор, а также неточности изготовления отдельных элементов и сборки конструкции в целом вызывают в статически неопределимых системах появление дополнительных усилий. При этом в статически определимых системах указанные факторы вызывают только перемещения. Эти дополнительные усилия зависят от геометрических размеров поперечных сечений и свойств материала. Пример 4. Статически неопределимая задача деформации растяже-ния-сжатия
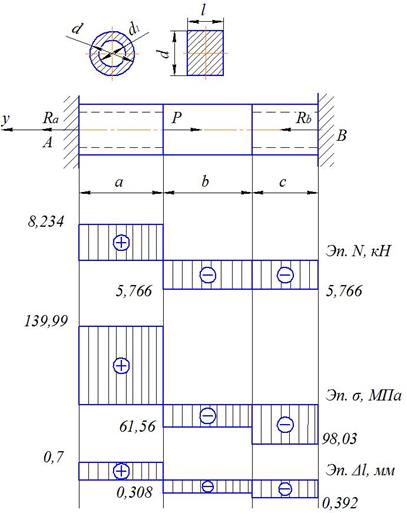
Для бруса (рис. 3.16 а), имеющего различные площади поперечных сечений участков и находящегося под действием продольных сил, используя метод сечений, построить эпюру нормальных сил N (y). Из условия прочности определить диаметры круглых поперечных сечений. Построить эпюры нормальных напряжений σ(y) и абсолютных деформаций отдельных участков бруса Δℓ(y). Принять материал бруса – сталь с допускаемым напряжением [σ] = 140 МПа и модулем продольной упругости Е = 2·105 МПа. Дано: a = 1,0; b = 1,0 м; c = 0,8 м; Р = 14 кН; d 1 / d = 0.6 и ℓ / d = 0,8 – относительные размеры поперечных сечений. Решение: 1.Определяем силы реакций в опорах А и В. Для этого наносим силы реакций в опорах на расчетную схему бруса (см.рис.3.16 а), произвольно выбирая их направления. Уравнение равновесия сил, направленных по оси y, имеет вид Σ y = 0; R а – Р + R b = 0. В уравнении равновесия два неизвестных – это силы реакций в опорах R а и R b, следовательно, задача является один раз статически неопределимой.
Рис. 3.16. Пример расчета статически неопределимой конструкции, находящейся под действием продольных сил: а – расчетная схема бруса переменного поперечного сечения; б – эпюра внутренней нормальной силы N(y); в – эпюра нормального напряжения σ(y); г – эпюра продольных перемещений сечений бруса Δℓ (y) Для раскрытия статической неопределимости составляем уравнение совместности деформаций: ΣΔℓ = ΣΔℓР + ΣΔℓΔТ +Σ∂, где ΣΔℓ – суммарная продольная деформация всех элементов конструкции; ΣΔℓР =
В уравнении совместности деформаций действуют следующие правила знаков: 1. Силовые деформации считаются положительными, если элемент конструкции испытывает растяжение, отрицательными – сжатие. 2. Температурные деформации считаются положительными, если элемент конструкции нагревается (т.е. удлиняется), отрицательными – охлаждается (т.е. укорачивается). 3. Монтажные деформации считаются положительными, если элемент конструкции изготовлен бОльшей длины, чем его номинальный размер по сборочному чертежу, и допуск на размер длины элемента положительный (т.е. чтобы собрать конструкцию в целом необходимо приложить дополнительное усилие), отрицательными – допуск на размер длины элемента отрицательный. Учитывая, что в условии задачи отсутствуют изменения температуры бруса в целом и неточности изготовления отдельных элементов бруса, нет информации о сборке, рассматриваем только силовые деформации различных по поперечному сечению элементов бруса. Составить уравнение совместности силовых деформаций бруса возможно двумя способами, мысленно представляя конструкцию в деформированном виде: 1. Мысленно отбрасывая опору В. 2. Мысленно отбрасывая опору А. Очевидно, что результаты вычисления сил реакций при использовании этих двух способов составления уравнений совместности деформации должны быть одинаковыми. Способ 1 Мысленно отбрасываем опору В и представляем брус (см.рис.3.16 а) в деформированном виде. При этом сила реакции R b становится внешней силой. Уравнение совместности силовых деформаций бруса, учитывая растяжение или сжатие отдельных элементов:
где
Решая уравнение совместности силовых деформаций бруса, получим
Способ 2 Мысленно отбрасываем опору А и представляем брус (см.рис.3.16 а) в деформированном виде. При этом сила реакции R а становится внешней силой. Уравнение совместности силовых деформаций бруса, учитывая растяжение или сжатие отдельных элементов:
Проверка 1: двумя способами получен одинаковый результат силы реакции Rb, следовательно, решение задачи можно продолжать. 2.Определение внутренних нормальных сил Стержень имеет три участка, границами которых служат границы различных по форме или размеру поперечных сечений («кольцо»–«прямоугольник»–«кольцо») (см.рис.3.16). Для обнаружения нормальных сил на этих участках используем метод сечений. Мысленно рассекаем стержень на каждом из участков на произвольных расстояниях y 1, y 2, y 3, y 4 и рассматриваем равновесие одной из частей рассеченного стержня, заменяя действие отброшенных частей внутренними нормальными силами N1 , N2, N3 (рис. 3.17 а, б, в, г). Для сечения I-I: Σ yI = 0; N1 = Ra = 8,234 кН. Для сечения II-II: Σ yII= 0; N2 = Ra – P = 8,234 – 14 = –5,766 кН. Для сечения III-III: Σ yIII= 0; N3 = Ra – P = 8,234 – 14 = –5,766 кН.
Проверка2:Правильность вычислений проверяем, рассматривая относительно сечения III - III правую часть стержня (рис.3.17 г). Для сечения III-III′: Σ yIII′= 0; N3′ = –Rb = –5,766 кН, т.е. результат одинаковый. При построении эпюр N(y)(рис.3.16 б) принимаем во внимание, что выражения для определения значений внутренних нормальных сил N1, N2, N3 не зависят от соответствующих расстояний y1, y2, y3 расположения поперечных сечений I-I, II-II, III-III, т.е. по всей длине соответствующих участков стержня значения N1, N2, N3 постоянны.
Рис. 3.17. Метод сечений для определения внутренних нормальных сил N: а – определение N1 ; б – определение N2; в, г – определение N3 3. Определение диаметров сечения бруса Из условия прочности бруса по нормальным напряжениям σ находим для каждого рассматриваемого участка отношение N/F, Н/мм2: Участок I: Участок II: Участок III: Максимальное значение N/F получили для участка I – «опасного сечения», где наиболее вероятно разрушение стержня от действия максимального по модулю нагружения бруса. Применим условие прочности: или Тогда а площади поперечных сечений стержня
4. Построение эпюры нормальных напряжений σ (y). Вычисляем напряжения в поперечном сечении для каждого участка бруса: Участок I: σ1= Участок II: σ2= Участок III: σ3= При построении эпюр σ(y)(рис.3.16 в) принимаем во внимание, что выражения для определения значений нормальных напряжений σ1, σ2, σ3 не зависят от соответствующих расстояний y 1, y 2, y 3 расположения поперечных сечений I-I, II-II, III-III, т.е. по всей длине соответствующих участков стержня значения σ1, σ2, σ3 постоянны. 5. Построение эпюры абсолютных деформаций отдельных участков бруса Δℓ(y). Для построения эпюры абсолютных деформаций Δℓ(y) используем закон Гука
Если нормальная сила N− постоянная величина, то Δℓ = Участок I: Δℓ1 = Участок II: Δℓ2 = Участок III: Δℓ3 = По полученным значениям строим эпюру абсолютных деформаций (удлинения, укорочения) отдельных участков бруса Δℓ(z) (см. рис.3.16 г). Определение перемещений сечений бруса начинаем с неподвижного закрепленного конца. Сечение в точке А расположено в заделке, оно не может смещаться и его перемещение равно нулю. ΔА=0. Участок I: Δ1 = Δℓ1= 0,70 мм. Участок II: Δ2 = Δℓ1+Δℓ2 = 0,70 – 0,308= 0,392 мм. Участок III: Δ3= Δ2 + Δℓ3 = 0,392 – 0,392= 0.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.24.134 (0.034 с.) |
 – суммарная деформация элементов конструкции от действия внешних нагрузок и/или внутренних усилий (силовые деформации), мм; Р – внешняя нагрузка и/или внутреннее усилие, действующие на элементе конструкции, Н; ℓ – длина элемента конструкции, мм; Е – модуль продольной упругости материала элемента конструкции, МПа= Н/мм2 ; F – площадь поперечного сечения элемента конструкции, мм2; ΣΔℓΔТ=α⋅ΔТ⋅ℓ – суммарная деформация элементов конструкции от измене-ния температуры (температурные деформации), мм; α – коэффициент линейного теплового расширения материала элемента конструкции, °С-1; ΔТ – изменение температуры элемента конструкции, °С; Σ∂ – суммарная деформация элементов конструкции от неточностей изготовления и их монтажа, фактически суммарный допуск на изготовление линейных размеров элементов конструкции (монтажные деформации),мм.
– суммарная деформация элементов конструкции от действия внешних нагрузок и/или внутренних усилий (силовые деформации), мм; Р – внешняя нагрузка и/или внутреннее усилие, действующие на элементе конструкции, Н; ℓ – длина элемента конструкции, мм; Е – модуль продольной упругости материала элемента конструкции, МПа= Н/мм2 ; F – площадь поперечного сечения элемента конструкции, мм2; ΣΔℓΔТ=α⋅ΔТ⋅ℓ – суммарная деформация элементов конструкции от измене-ния температуры (температурные деформации), мм; α – коэффициент линейного теплового расширения материала элемента конструкции, °С-1; ΔТ – изменение температуры элемента конструкции, °С; Σ∂ – суммарная деформация элементов конструкции от неточностей изготовления и их монтажа, фактически суммарный допуск на изготовление линейных размеров элементов конструкции (монтажные деформации),мм.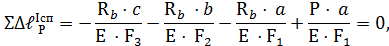
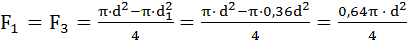 = 0,16
= 0,16 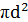 ;
; .
.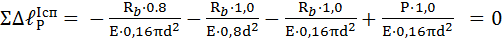 ,
,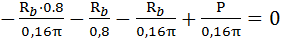 ,
,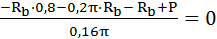 ,
, ,
,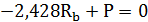 ,
,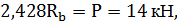
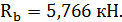
 ,
,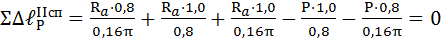 ,
,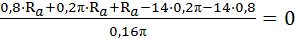 ,
, ,
,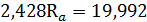
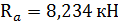
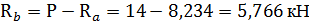
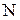 методом сечений
методом сечений 
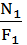
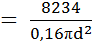 .
. 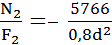 .
.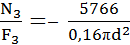 .
.
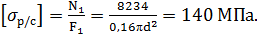
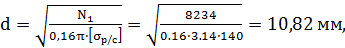
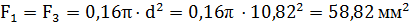 ,
, .
.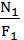 =
= 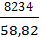 =139,99 МПа
=139,99 МПа 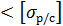 =140 МПа, т.е. на участке I условие прочности выполняется – конструкция работоспособна.
=140 МПа, т.е. на участке I условие прочности выполняется – конструкция работоспособна.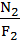 =
= 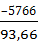 = – 61,56 МПа
= – 61,56 МПа 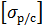 производим по модулю σ2, т.е. условие прочности выполняется – конструкция работоспособна.
производим по модулю σ2, т.е. условие прочности выполняется – конструкция работоспособна. =
= 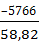 = – 98,03 МПа
= – 98,03 МПа 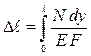 .
.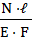 .
. =
= 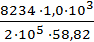 = 0,70 мм.
= 0,70 мм.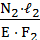 =
=  = – 0,308 мм.
= – 0,308 мм.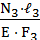 =
= 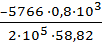 = – 0,392 мм.
= – 0,392 мм.


