Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод: уравновешивающая сила определена верно.
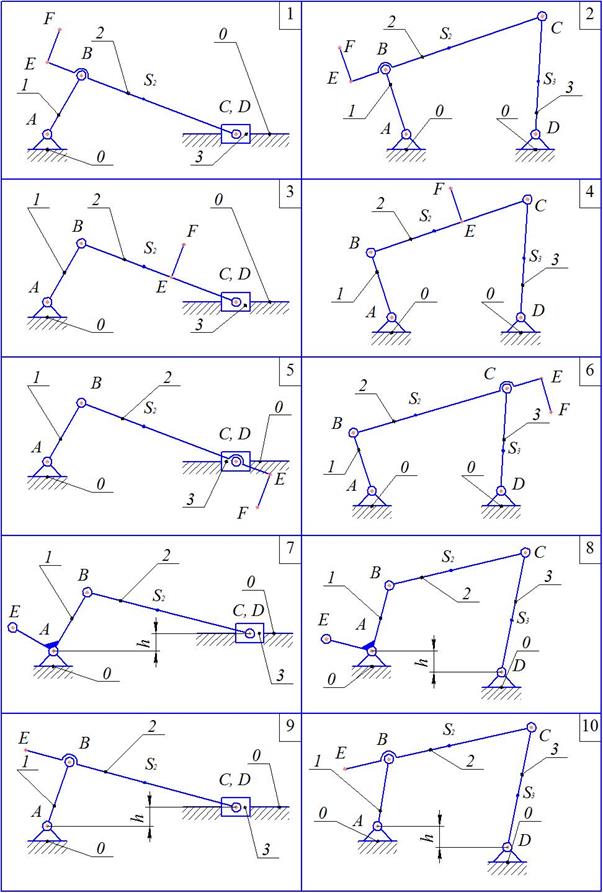
Задание №1 для курсового проектирования «Кинематический и силовой анализ плоских рычажных механизмов» Для плоского рычажного механизма, положение звеньев которого задано углом поворота ведущего звена 1 – кривошипа АВ (рис. 2.32), выполнить структурное, кинематическое и силовое исследование. Силами инерции ведущего звена 1 можно пренебречь. Кинематическое исследование выполнить графоаналитическим методом. Силовой анализ начального механизма выполнить двумя способами: 1) с помощью плана сил; 2) с помощью теоремы о «жёстком» рычаге Н.Е. Жуковского. Дано: 1).Схема механизма (рис. 2.32). Положением кривошипа 1 (АВ)и направлением его вращения задаться самостоятельно. 2). n 1,об/мин – частота вращения ведущего звена 1 механизма – кривошипа АВ. 3). LAB, LBC и т.д. – длины звеньев механизма. 4). Положения неподвижных шарниров, направляющих, центров тяжести. 5). P 2, P 3 – величины силы веса шатуна 2 и коромысла (ползуна) 3. 6). Р пс– величина силы полезного сопротивления, приложенной к точке С и направленной в сторону, противоположную линейной скорости этой точки. Примечание: Задание №1 курсовой работы состоит из расчетно-пояснительной записки и графических построений. Графические построения выполняются карандашом на отдельном листе миллиметровой бумаги формата А3 с соблюдением требований ГОСТ 2.301-68. На чертежах указываются масштабы и пояснительные надписи к построениям. Все вспомогательные построения на чертежах обязательно сохраняются.
Примечания: 1. Длина ℓ AE – только для схем 7-8;2.Длина h – только для схем 7-10; 3. Длины ℓ СD, ℓ AD,
Рис.2.32. Схемы механизмов для кинематического и силового анализа Глава 3 ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ Ведение в сопротивление материалов Сопротивление материалов – наука о прочности, жесткости и устойчивости элементов конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, надежные размеры деталей машин и различных строительных сооружений. Основные положения сопротивления материалов опираются на законы и теоремы общей механики, математики и физики. Основной базой является теоретическая механика, которая изучает равновесие и движение абсолютно твердых тел. В отличие от теоретической механики, в сопротивлении материалов рассматриваются деформируемые тела, которые могут менять размеры и форму под действием внешних сил.
Объекты курса Любая конструкция состоит из различных элементов. Эти элементы конструкций могут быть: 1. Брус (стержень). Брусом называется твердое тело, одно из измерений которого (длина) значительно превышает размеры поперечного сечения (рис. 3.1 а). 2. Оболочка, пластина. Оболочкой называется твердое тело, одно измерение которого (толщина) мало по сравнению с двумя другими (рис. 3.1 г). Геометрическое место точек, равноудаленных от наружной и внутренней поверхностей оболочки, называется срединной поверхностью. Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной (рис. 3.1 б, в). 3. Массив. Все три измерения одного порядка (рис. 3.1 д). В сопротивлении материалов главное внимание уделяется расчету стержней (брусьев). Расчетами пластин, оболочек, массивов занимается теория упругости.
 
Рис. 3.1. Модели формы элементов конструкции: а – стержень; б – кольцо; в – круглая пластинка; г – оболочка; д – массив Внешние силы Если конструкция рассматривается изолированно от окружающих тел, то действие последних на конструкцию заменяется силами, которые называются внешними. Сосредоточенные силы – передаются на конструкцию через небольшую площадку, то есть можно практически условно считать, что они приложены в точке (рис. 3.2). К числу таких сил можно отнести давление колеса на рельс и т. д. Из приведенного примера видно, что понятие сосредоточенной силы является условным. Одна и та же нагрузка в зависимости от поставленной задачи может быть схематизирована по-разному.
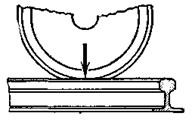
Рис. 3.2. Пример сосредоточенной силы Распределенная нагрузка – передается на сооружение через определенную площадь и измеряется в единицах силы, отнесенной к единице площади (кН/м2, кН/см2, Н/мм2). К числу таких нагрузок относится давление сыпучих материалов и жидкости на стенки резервуаров (рис. 3.3 а), давление воды на пластину (рис. 3.3 б) и т. п.
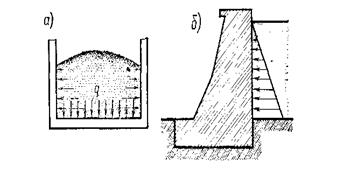
Рис. 3.3. Примеры распределенной нагрузки: а –сыпучих материалов; б –жидкостей
Для стержневых систем распределенную по площади нагрузку Р (рис. 3.4 а) обычно заменяют погонной q (рис. 3.4 б): q = P · b, где q – погонная нагрузка; Р – нагрузка, распределенная по площади; b – ширина балки.
По времени действия нагрузки подразделяются: на статические – нагрузки, приложенные к сооружению довольно медленно, когда ускорениями масс сооружений, а следовательно, и силами инерции можно пренебречь; на динамические – нагрузки, изменяемые во времени: удар копра, несбалансированный двигатель. Эти нагрузки дают динамический эффект, когда ускорениями движения масс пренебречь нельзя, а следовательно, нужно учесть силу инерции.
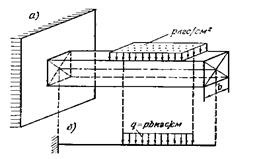
Рис. 3.4. Замена нагрузки: а – распределенная по площади; б – погонная Основные понятия и гипотезы (допущения) Под действием внешних нагрузок отдельные частицы тела перемещаются относительно друг друга. Как следствие, тело изменяет свои размеры и форму. Эти изменения и называются деформацией.
Если силы, вызвавшие деформацию, уменьшать и затем полностью снять, то тело будет стремиться приобрести первоначальную форму. Деформации полностью или частично исчезнут. Свойство тел деформироваться под нагрузкой и затем после устранения сил восстанавливать свое первоначальное состояние называют упругостью. Часть деформации, которая исчезает после снятия нагрузок, называют упругой, а ту часть, которая остается, называют остаточной деформацией. Появление остаточной деформации связано с так называемой пластичностью. У некоторых материалов упругие свойства одинаковы во всех направлениях. Такие тела называют изотропными. Наряду с этим встречаются анизотропные тела, у которых свойства в различных направлениях разные. Сопротивление материалов рассматривает идеализированное тело (абстрактное) и наделяет его определенными свойствами. Принимается гипотеза о сплошном и однородном строении материала. Под сплошным понимаем материал, который не имеет никаких пустот, что позволяет применять анализ бесконечно малых величин. Под однородностью понимается то, что механические свойства тела в окрестностях точки не зависят от размеров рассматриваемого элемента.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.171.136 (0.023 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
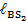
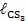
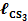– только для схем 2, 4, 6, 8, 10.
