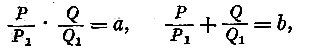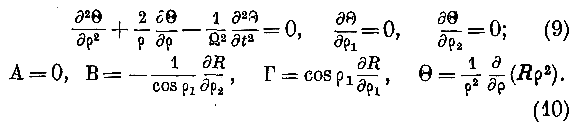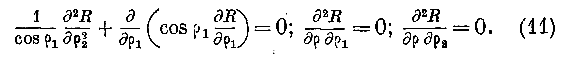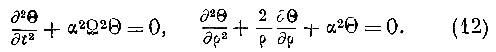Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Законы поперечных колебаний. § 12. Интеграция в случае колебаний по одной из ланий кривизны
§ 12. Интеграция в случае колебаний по одной из ланий кривизны. Существуют многие волновые поверхности, допускающие колебания по одной из линий кривизны, причём на всей волновой поверхности колебания но другой липни кривизны не существуют. Такие колебания мы будем называть прямолинейно поляризованными по одной из линий кривизны, причём плоскость поляризации мы считаем перпендикулярною к плоскости колебаний. Чтобы отыскать условия, которые должны быть выполнены, нам остаётся положить или Лг или /?, равными нулю. Мы примем последнее. Следовательно, в уравнениях (9) и (10) нам нужно положить и = 0, вследствие чего они преобразуются в следующие:
Полагая в этих уравнениях H — i и дифференцируя уравнения (49) — первое по р, второе по p 1; третье по ра, находим: Подставляя эту величину в уравнение (50), находим, что оно обращается в тождество. Подставляя величину и в уравнения (48), находим:
Дифференцируя последнее из этих уравнений по ^ и обращая внимание на первое из уравнений (49), имеем:
Вот условие, которому должна удовлетворять поверхность волны, чтобы колебание по нормали к поверхности р1 могло не существовать. Раскроем это условие. Мы имеем:
Означая через л, ^ две функции, зависящие от одного р2, мы удовлетворим предыдущим уравнениям, полагая Рг = Р\, $, = ф, (56) Но мы видели в § 3, что
Подставляя в эти выражения величины P, u Qi из уравнений (56), мы находим:
А это свойство, как оыло доказано выпад (§ '.t, с), принадлежит одной сфере, если только одно из уравнений (57) не обращается в тождество, например первое, что возможно, когда m i i Но при настоящих условиях равенство ~ = р. = ~- тем не менее остается, и так как Рг и Р, а следова- Р тельно, и —-1 не зависят от р2> т° p- = const., и мы снова приходим к сфере. Чтобы избежать этого частного случая, мы должны предположить, что второе из уравнений (57) обращается в тождество, что возможно, когда
ибо второе из уравнений (56) даёт:
Легко убедиться, что эти выражения обращают u тождество последнее из уравнений (49). Обращаясь к уравнениям (7), мы находим следующие т:-?личины для кривизны ортогональных поверхностей:
Следовательно, поверхность с параметром ^ есть плоскость. Ни один из радиусов кривизны других поверхностей не изменяется с переменой pj. Для всех точек пересечения поверхностей p и р2 кривизна этих поверхностей не изменяется.
Итак, поперечные колебания по одной линии кривизны могут совершаться только на поверхности волны, характеризуемой выражениями (61), и притом эти колебания перпендикулярны к плоскостям, параметр которых есть рг, т. е. поляризованы в этих плоскостях. К рассматриваемым поверхностям относятся поверхности вращения и цилиндры. Для них
Следовательно, для цилиндров, за исключением круглого, колебания могут совершаться только параллельно образующей; для поверхностей вращения, за исключением сферы п круглою цилиндра, - только перпендикулярно меридиональным плоскостям. Чтобы колебания могли совершаться и по другой линии кривизны, необходимо, чтобы одновременно с условиями (63) существовали ещё условия, которые, как легко убедиться, выполняются только сферой или круглым цилиндром. Отсюда заключаем, что на поверхностях вращения и цилиндрах колебания могут совершаться только по одной линии кривизны, положение которой нами уже указано. То же самое мы скажем п о поверхностях (61), так как, чтобы колебание могло происходить по другой липни кривизн“, мы дошли бы до заключения, что Л и р. должны быть функциями;^, но они должны быть u функциями (>2, следовательно, X=const., [>. = const., п мы впадаем в случай сферы пли круглого цилиндра. Теперь остаётся исследовать самый вид поперечных колебаний. Подставляя величины А' и В' во второе из уравнений (49), которое одно осталось неудовлетворённым находим, полагая ff -i:
Подставляя в это выражение величины a lt Н% (61), легко видеть, что оно не будет содержать pj. Полагая в этом уравнении
преобразуем его в следующее:
Итак, решение вопроса зависит от успешности интеграции этого уравнения с частными производными. Предыдущее исследование даёт нам возможность разделить все волновые поверхности на три группы: a) Поверхность волны и соответствующая ей орто Эти поверхности не допускают прямолинейной поляризации ни по одной из линий кривизны. b) Изотермические волновые поверхности. Эти поверхности не допускают прямолинейную поляризацию, безраз.лично, по той или другой линии кривизны.
c) Поверхности, удовлетворяющие условиям (61), Эти поверхности допускают прямолинейную поляризацию в плоскостях, принадлежащих семейству ортогональных поверхностей. Прямолинейная поляризация в плоскостях перпендикулярных невозможна. III. КОЛЕБАНИЯ ПРОДОЛЬНЫЕ § 13. Обращаясь к основным дифференциальным уравнениям колебаний в § 7, мы заметим, что когда умножим их на — = к,2, они будут содержать члены, из которых одни имеют коэффициентом квадрат скорости и поперечных колебаний, другие-квадрат скорости продольных колебаний. Первые
Так как поверхность p по нашему выбору есть поверхность волны, то в уравнениях § 7 мы должны удержать одно колебание R и приравнять нулю колебания /?! и R.2, совершающиеся в плоскости, касательной к волне. Вследствие этого находим, полагая //=1:
Так как А = 0, то уравнения (1) примут вид:
Умножая первое из уравнений (2) на //i//2, дифференцируя по p и обращая внимание на уравнение (4), находим: Но но уравнениям (2) В не зависит ни от рх, ни от [-,. Следовательно, означая через &F частную производную от функции F по одной из переменных ^, р.2, мы получаем пз уравнения (7):
Подставляя в ото выражение величавы II lt Н2, найденные в § 3, приравнивая нулю коэффициенты при различных степенях,., мы находим следующие условия, которым должна удовлетворять волновая
Но мы знаем, что подобные соотношения имеют место только для сферы, круглого цилиндра и плоскости. Отсюда заключаем, что одни изотермические волновые поверхности могут распространять колебания продольные. Итак, если поверхность сотрясения или начальная волна не принадлежат к поверхностям изотермических волн, то вблизи их колебания происходят смешанные; но на значительных расстояниях волна приближается к виду одной из изотермических волн, и в явлении обнаруживаются колебания продольные. Это заключение было выведено иным путём Пуассоном. Нам остается объинтегрировать приведенные дифференциальные уравнения для сферы. Для сферы в координатах, уже нами употреблённых, мы имеем:
Подставляя величины В и Т в уравнение (5), получаем:
где суммирование совершается но индексу к. Подставляя величину 0 в последнее из уравнений (10), интегрируя u обращая внимание на уравнение (11), находим:
Последний член этого выражения должен равняться нулю, ибо при p =оо будет /2 = 0. Второй член второй части выражения R отпадает для (> различных, и квадрат амплитуды, т. е. напряжение звука, изменяется обратно пропорционально квадрату расстояния. Между тем квадрат амплитуды кубического расширения следует тому жо закону для всякого р. Все эти выводы были получены Пуассоном иным путём.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 33; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.116 (0.02 с.) |





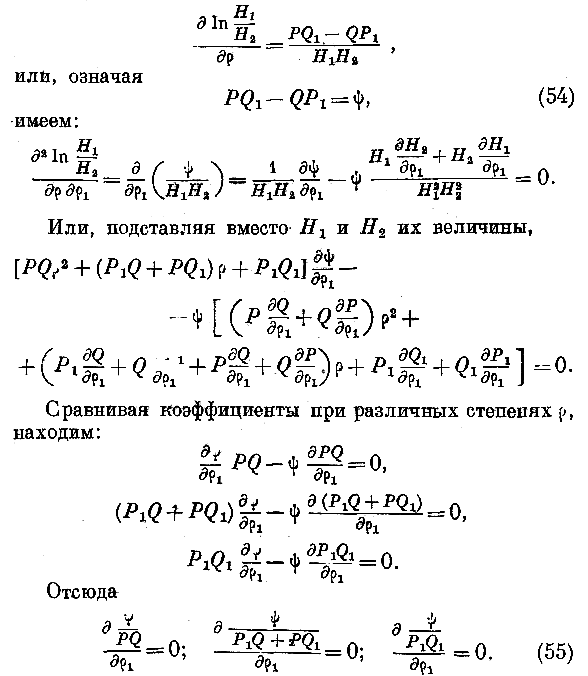
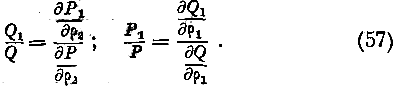



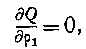







 члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу:
члены в случае колебаний продольных должны исчезнуть из уравнений, и мы получаем первую группу: