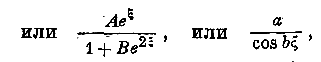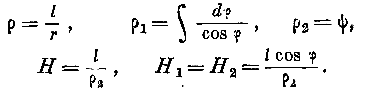Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аконы колебании в неограниченной среде постоянной упругости
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.) § 2. Приложим приведённые выражения к случаю волны, распространяющейся в среде постоянной упругости. Её поступательное движение совершается с постоянной скоростью, следовательно, если представим себе два бесконечно близких положения волны, то отрезки нормалей ds, заключающиеся между ними, будут величинами, постоянными для всех точек волновой поверхности. Итак,
Или обращаясь к уравнению (1)
Это основные уравнения в нашем исследовании. С их помощью ур-ния (2) дают
Кривизна 1/p дуги s будет по уравнениям (3) и (7)
Этот результат известен: линия s, пересечение поверхностей μ1 и μ2, есть прямая, нормальная к поверхностям (”; эта нормаль имеет здесь значение луча. Отсюда вытекает естественный выбор параметра р. Он может представлять отрезок луча между некоторым начальным и настоящим положением волны. При таком выборе ds = d\> и по уравнению (1) имеем Я = 1. Итак, мы имеем теорему: Если принимаем за параметр волны отрезок луча между начальным и последующим положением волны, то её дифференциальный параметр первого порядка есть во всём пространстве величина постоянная и равная 1. § 3. Выражения (4) и (5) вследствие уравнений (6) преобразуются в следующие:
где P и Q означают функции, не зависящие от {>. Подставляя эти выражения в формулы (7), находим: Нг = — Рг', //2 = —<?"", т. е. дифференциальные параметры первого порядка поверхностей, ортогональных к волне, пропорциональны радиусам кривизны волны.
Интегрируя выражения (11) и означая через PL и Ql две новые функции, не зависящие от р, получаем: Подставляя в эти выражения величины Нл и Нг из уравнений (12), мы преобразуем их в следующие:
Подставляя выражения (13) в последнее из уравнений (10), мы находим:
Итак, условия ортогональности рассматриваемой си § 4. Мы переходим к исследованию некоторых частных видов дифференциальных параметров первого порядка поверхностей р, рг, |.,. а) Предположим, что поверхность p есть поверхность вращения. Принимая ось вращения за ось z, называя через г расстояние точки поверхности от оси, через рг — угол меридиональных плоскостей с постоянною плоскостью, через рг— параметр поверхностей, пересекающих поверхности p и р2 под прямым углом, мы имеем, полагая p постоянным:
Замечая, что находим по уравнению (1):
Точно так же имеем:
Следовательно, Нг и На в поверхностях вращения не зависят от параметра меридиональных плоскостей. Ь) Рассмотрим цилиндрические поверхности. Возьмём ось z параллельно образующей. Координату z примем за параметр плоскостей, нормальных к оси z. Параметр плоскостей, параллельных оси z и нормальных к поверхности цилиндра, которую принимаем за поверхность [>, означим через f/t. Имеем, полагая p постоянным:
откуда находим:
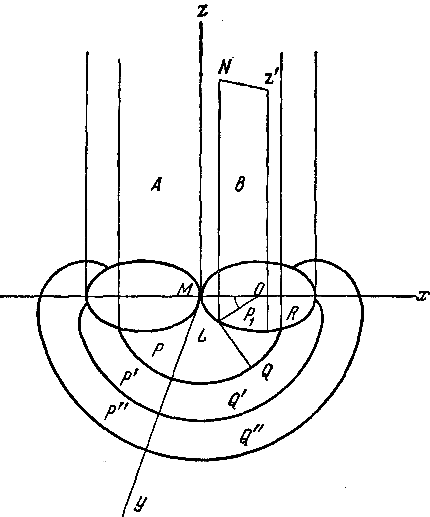
В обоих случаях (а) и (Ь), как легко видеть, первое из уравнений (14) обращается в тождество, и уравнение (15) сводится к двум последним членам. Как пример цилиндрической волны рассмотрим эпициклоидалы-гый цилиндр. Представим себе (рис. 1) в среде постоянной упругости два равных неограниченных круглых цилиндра А и В. Оба цилиндра образуют по линии MZ узкую щель, параллельную их осям и через которую вытекают колебания в пространство, находящееся перед цилж:-.драми. От этой щели побегут колебания, огибая до ы>- которой точки L один из цилиндров и затем распространяясь по касательной к нему LQ. Таким образом, от MZ побежит цилиндрическая волна, сечение которой, перпендикулярное к образующей, представит кривая PQ. Эту последнюю мы можем себе представить происшедшей от движения конца нити MR, навёрнутой на щь
Рис. 1. линдp В и затем развёртываемой при постоянном натяжении. Длина этой нити может быть принята за параметр р, так как все колебания, одновременно вышедшие из MZ, будут одновременно прибывать к различным поверхностям р. Для некоторого момента сечение волны будет P'Q', для другого P"Q" и т. д. Если примем радиус цилиндров равным 1, угол MOL —sä параметр pt касательных плоскостей. NLQZ', нормаль- ных к волне, то геометрические свойства волны представятся уравнениями:
с) Исследуем поверхность, для которой
Означая это отношение через и,, мы находим из уравнений (14):
Интегрируя, получаем:
Это равенство возможно, если только (j. постоянно. Поэтому уравнения (12) примут вид:
И из уравнений (2) мы находим величину кривизн поверхности р:
т. е. оба радиуса кривизны равны между собою в каждой точке поверхности p и не изменяются при переходе от одной точки к другой. Следовательно, в рассматриваемом случае поверхность p есть сфера. Сюда же относится случай
если одно из уравнений (14) не обращается тождественно в нуль, что приводит к круглому цилиндру. Если мы примем //=1, получим:
Вместо p -l u. мы можем поставить просто p при условии, что при р = 0 будет /fj —0, /7о=--0. Тогда Нг = Рр, HZ = Q?. Принимая р2 за параметр меридиональных плоскостей, рг — за параметр конуса широты и p--за радиус сферы, мы получаем из выражений (11):
Следовательно,
d) Исследуем поверхность волны р, когда одна из величин Р1 пли Q-^ обращается в нуль. Примем <?1 = 0- Кривизны поверхности р определяются из уравнений (7), и мы находим:
откуда заключаем, что один радиус кривизны есть величина, постоянная для всех точек поверхности р, другой же — величина переменная. Следовательно, поверхность р имеет вид канала, образованного движением центра сферы постоянного радиуса г" по некоторой кривой в пространстве.
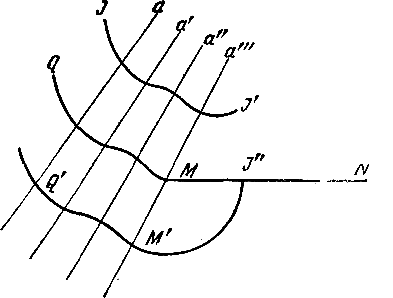
Так как 01=0, то из уравнений (14) мы находим, что />! не должно зависеть от \-г и Q не должно зависеть от р!. Поэтому кривизны поверхностей ръ ра будут по выражениям (7): е) Явления оиффракции. При своём движении волна может встречать препятствия, которые она должна огибать, или отверстия, через которые может проникнуть только часть волны. Как в том, так и в другом случае явления изменяются, ибо изменяется самый вид волны. Предположим (рис. 2), что //' представляет поверхность волны в какой-нибудь момент времени.
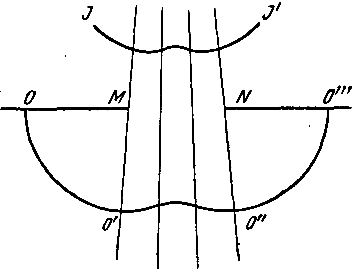
Рис. 2. MN представляет препятствие. Линии а, а', а", а'" представляют направление нормалей к волне. В некоторый момент волна принимает положение QM, затем Q'M'J", ибо движение распространилось и в пространстве M'MN. Сечение поверхности M'J" плоскостью, нормальною к ребру препятствия MN, есть дуга круга. Следовательно, эта поверхность принадлежит к разряду исследованных в (d). Излагаемая ниже теория поперечных колебаний даёт возможность по данному виду волны определить законы колебаний, происходящих на её поверхности; а следовательно, определяя дифференциальные параметры первого порядка ортогональной системы, включающей поверхность Q'M'J", вставляя их в найденные выше дифференциальные уравнения с частными производными и интегрируя их, мы решим задачу. Пусть //' (рис. 3) представляет снова начальное положение волны и MN —отверстие- Легко видеть, что одним из последующих положений волны будет 00'0"0'", где 00', О"О'" суть поверхности, определённые в (d). Такой случай решается, как и предыдущий. Метод изыскания законов диффракции, здесь предложенный, представляет к своему осуществлению многие трудности, заключающиеся преимущественно в разрывности всех или некоторых дифференциальных параметров первого порядка ортогональной системы. В этой разрывности заключается основной характер явлений диффракции.
Рис. 3. § 5. Мы переходим к исследованию изотермических поверхностей. Предположим, что поверхность волны есть поверхность изотермическая и p — её термометрический
параметр. Означая через ренциалъныи параметр второго порядка функции р/; имеем: А2р = 0, так как p есть параметр термометрический. Следовательно,
откуда
Вставляя в это выражение величины //,, 7/: из уравнений (12), находим:
Это выражение должно существовать для всяких р, рь р2. Мы можем удовлетворить ему при двух предположениях:
! g постоянное. Рассмотрим первое предположение. Мы находим:
Предполагая, что P и Q ые обращаются в нуль, мы находим из двух последних уравнений: Pl = 0, Q, = 0. Следовательно, рассматриваемая поверхность есть сфера. Величина //, выраженная термометрическим параметром, б\'пет:
Если же мы примем Т3 —0, то должны будем принять или JP1 = 0, то-есть Н1 = 0, что невозможно, или Q = 0, но тогда равенство P1Ql = 0 даёт или Рг == 0, или (>1 = 0, то-есть опять или Н1 = 0 или 7/2=0, что невозможно. Рассмотрим второе предположение. Оно влечёт за собою
Здесь возможны два случая: Р=0, q! 0 или Q = Q, />i=0. Примем последнее. Из уравнений (12) имеем:
Нг = Р^Нар, ffa = Qi. Но Elf // = е я. Следовательно, Bi~gPe>.; Я2 = <?1-
Так как Q=-0, /^ = 0, то из уравнений (14) находим: 9Р_ ___ n “5Q! __ л - — V/j n — • v/, <??2 5?! следовательно, Обращаясь к уравнениям (7), мы находим следующие выражения для кривизны поверхностей р, р1( р2:
Отсюда ясно, что рассматриваемая поверхность есть не что иное, как круглый цилиндр. Итак, из всех изотермических поверхностей только плоскость, сфера и круглый цилиндр могут быть поверхностями волны. § 6. Исследование поверхностей;., ьг, о2) когда две из них, например p и j^, или все три изотермичны, представляя случай более частный, чем предыдущий, не требует более определения вида поверхностей, которые не могут быть иными, чем сфера и круглый цилиндр, но сводится к определению функции P и Q или P и Qlt удовлетворяющих новым условиям. 'Мы рассмотрим только случай тройной изотермической системы ортогональных поверхностей, параметры которых \>, рь р2 будут термометрическими параметрами. Здесь к условию
нам нужно прибавить
Эти условия для сферы примут вид:
Следовательно, отношение
Итак, Уравнение (15) будет здесь:
Частные интегралы этого уравнения будут иметь вид
где s есть линейная функция относительно рь р2. Для полного определения вида функций Р, (ч, 1>2 нам следовало бы заняться интеграцией нового ряда дифференциальных уравнений с частными производными, выражающими зависимость криволинейных Координат от прямолинейных. Но таи как подобные вычисления были бы излишни в настоящем исследовании, то мы ограничимся приведением известных результатов.
Означая через г радиус сферы, через 9 — широту и Ф — долготу, имеем:
Для круглого цилиндра мы имели:
При новых условиях, вводимых свойствами тройной изотермической системы, мы получаем еще:
назад вперед
Знаете ли Вы, что такое мысленный эксперимент, gedanken experiment? Релятивисты и позитивисты утверждают, что "мысленный эксперимент" весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении. Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: "Если факт не соответствует теории - измените факт" (В другом варианте " - Факт не соответствует теории? - Тем хуже для факта"). Максимально, на что может претендовать "мысленный эксперимент" - это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте. Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем. Понятие "мысленный эксперимент" придумано специально спекулянтами - релятивистами для шулерской подмены реальной проверки мысли на практике (эксперимента) своим "честным словом". Подробнее читайте в FAQ по эфирной физике.
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 48; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.142 (0.048 с.) |


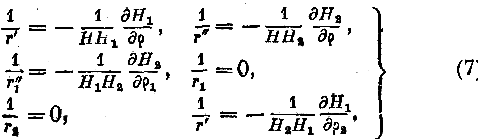
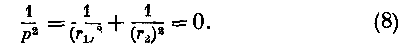
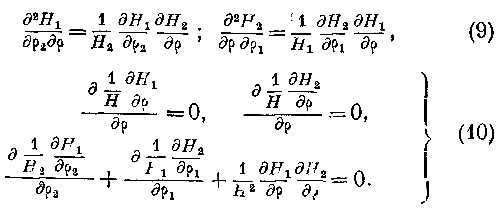


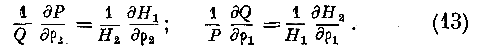
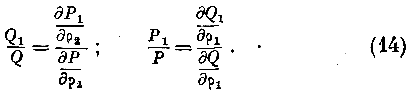
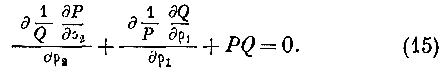

 мы
мы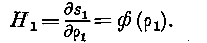
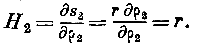

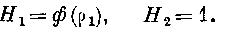
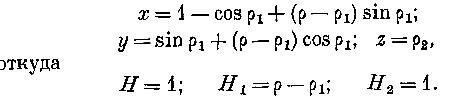
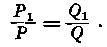


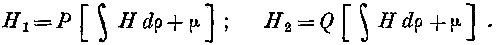
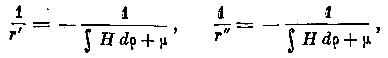

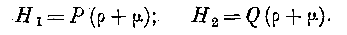
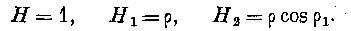


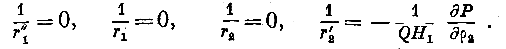
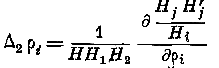
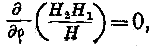




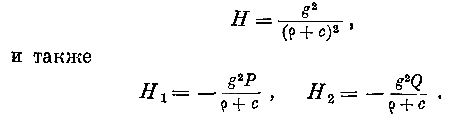
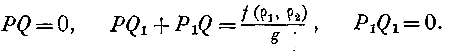

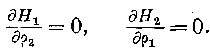
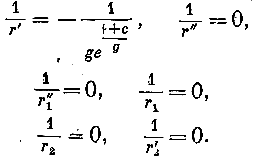

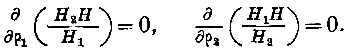
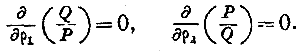
 есть величина постоянная, которую означим через -.
есть величина постоянная, которую означим через -.