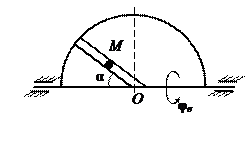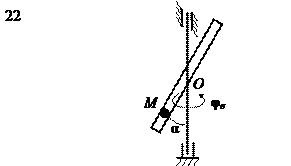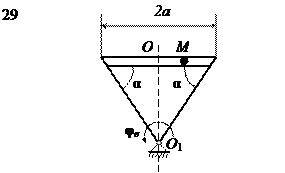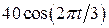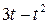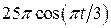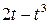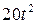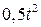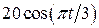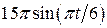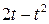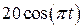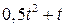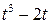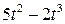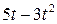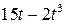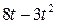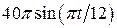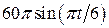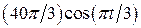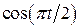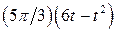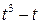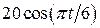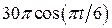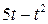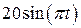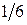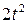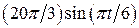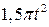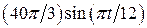Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 5. Определение абсолютной скорости и абсолютного ускорения точки при сложном движенииСодержание книги
Поиск на нашем сайте
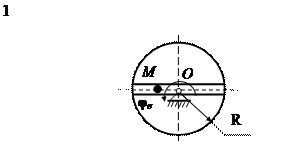
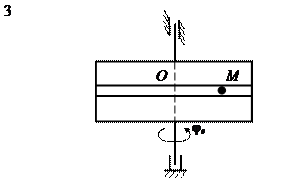
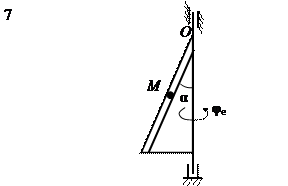
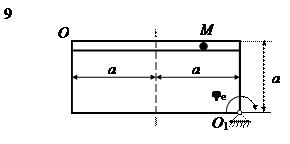
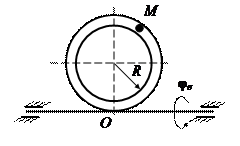
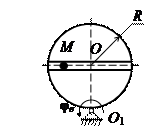
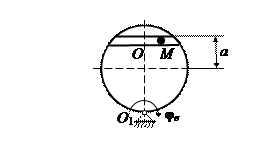
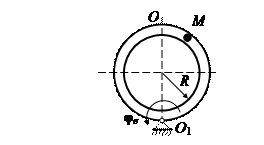
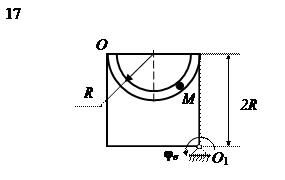
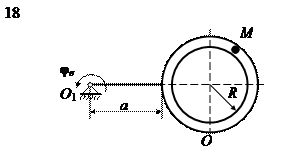
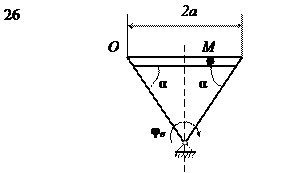
На рис. 15 (а, б, в) показано тело, совершающее вращательное движение по закону j е = f 1(t). По поверхности этого тела перемещается точка М по закону Sr = f 2(t). В момент времени t = t 1 найти абсолютную скорость и абсолютное ускорение точки М. Исходные данные приведены в таблице 8. Положение точки М показано при положительном значении естественной координаты ОМ. Указания В задаче рассматривается сложное движение точки. Согласно теореме о сложении скоростей абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
Величина абсолютной скорости:
Согласно теореме о сложении ускорений абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений:
Величина абсолютного ускорения определяется по проекциям на оси выбранной системы координат. Алгоритм решения задач: 1. Выбрать точку, движение которой рассматривается как сложное. Разложить абсолютное движение точки на относительное и переносное. Дать характеристику обоим движениям. 2. Выбрать подвижную и неподвижную системы отсчета. 3. Определить положение точки в заданный момент времени 4. Определить абсолютную скорость точки при 5. Определить абсолютное ускорение точки при Для расчетов абсолютной скорости и абсолютного ускорения необходимо выполнить отдельные рисунки. Пример решения задач Пластина вращается вокруг горизонтальной оси по закону Решение:
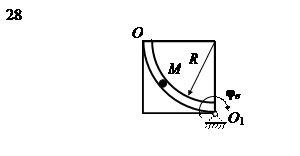
Рис. 14, а Рассмотрим сложное движение точки М. Относительным движением точки М является движение точки по дуге окружности радиусом R. Переносным движением системы является вращательное движение пластины вокруг горизонтальной оси. Переносным движением точки М является движение по окружности радиусом Re в плоскости, перпендикулярной оси вращения. Подвижную систему отсчета связываем с пластиной, неподвижную – с опорами оси вращения. Находим положение точки на пластине при t1 = 2 с: OM1 = 2,5pt12 = 2,5p·22 = 10p см; Определяем абсолютную скорость точки М 1 (рис. 14 а):
Здесь, относительная скорость точки М 1: При t1 = 2 с. Переносная скорость точки М 1: Здесь: При t1 =2 с.
Так как вектора
Определяем абсолютное ускорение точки M 1 (рис. 14 б):
Относительное ускорение складывается из касательного и нормального ускорений:
Так как
Переносное ускорение складывается из вращательного и центростремительного ускорений:
где При t 1 = 2 с
Рис. 14, б
Кориолисово ускорение:
Вектор Таким образом, векторное равенство для определения абсолютного ускорения имеет вид:
Проецируем его на оси системы координат М 1 xyz: ax = ae вр + ac = 623,52 + 596,6 = 1220,12 см/с2; ay = – ar t sin60o – arn cos60o = –15,71·0,866 – 32,87·0,5 = –30,04 см/с2; az = –ae ц + ar tcos60o – arn sin60o= –9378,78+15,71·0,5–32,87·0,866 = = –9399,39 см/с2.
Ответ:
Рис. 15, а
Рис. 15, б
Рис. 15, в
Таблица 8
Раздел «Динамика»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.95 (0.009 с.) |

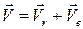 .
.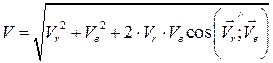 .
.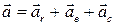 .
. .
.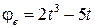 , рад. По криволинейному каналу радиуса R = 30 см, перемещается точка М по закону Sr = OM = 2,5p t 2, см (см. рис. 14 а). В момент времени t1 = 2 с найти абсолютную скорость и абсолютное ускорение точки.
, рад. По криволинейному каналу радиуса R = 30 см, перемещается точка М по закону Sr = OM = 2,5p t 2, см (см. рис. 14 а). В момент времени t1 = 2 с найти абсолютную скорость и абсолютное ускорение точки.
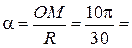
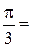 60º.
60º.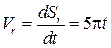 , см/с.
, см/с.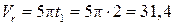 см/с. Так как
см/с. Так как  , вектор
, вектор 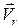 направлен в сторону положительного отсчета координаты
направлен в сторону положительного отсчета координаты  .
.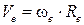 .
.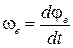 =
= 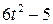 , с-1 – угловая скорость пластины.
, с-1 – угловая скорость пластины. =
=  с-1. Так как
с-1. Так как  >0, направление вращения
>0, направление вращения  .
.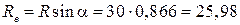 см.
см. см/с,
см/с, 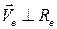 и направлен в сторону вращения
и направлен в сторону вращения 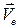 перпендикулярны друг другу, то
перпендикулярны друг другу, то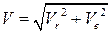 =
= 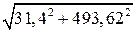 =
= 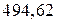 см/с.
см/с.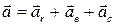
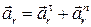 .
. =
= 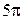 = 15,71 см/с2.
= 15,71 см/с2. , вектор
, вектор 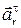 направлен в сторону положительного отсчета координаты
направлен в сторону положительного отсчета координаты 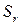 .
.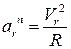 =
=  =
= 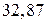 см/с2.
см/с2.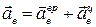 .
. ;
;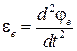 =
=  , с-2 – угловое ускорение пластины.
, с-2 – угловое ускорение пластины.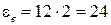 с-2. Так как
с-2. Так как 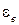 >0, направление вращения
>0, направление вращения 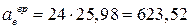 см/с2,
см/с2,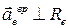 и направлен в сторону вращения
и направлен в сторону вращения 
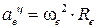 =
= 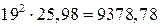 см/с2.
см/с2.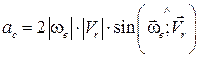 , где
, где  .
.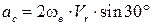 =
=  см/с2.
см/с2. направлен согласно правилу Жуковского или векторного произведения, т.е. перпендикулярно плоскости чертежа (вдоль оси x).
направлен согласно правилу Жуковского или векторного произведения, т.е. перпендикулярно плоскости чертежа (вдоль оси x).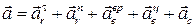 .
. =
= 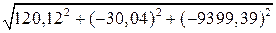 =
= 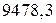 см/с2.
см/с2.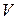 =
=