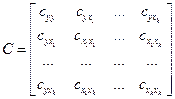Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы регрессионного анализаСодержание книги
Поиск на нашем сайте
Регрессия – аппроксимация графика рассеяния некоторой кривой. Такая кривая называется линией регрессии. Термин введен Фрэнсисом Гальтоном (Francis Galton, 1822-1911), который обнаружил, что сыновья высоких отцов в среднем ниже, чем их отцы, и назвал это регрессией посредственности. Линию регрессии обычно подбирают методом наименьших квадратов (МНК), т.е. таким образом, чтобы
В курсе ТВ мы рассматривали вывод одномерной регрессии (см. приведенное выше уравнение). Для одномерного случая уравнение для вычисления прогнозных значений можно записать в следующем виде
где
Таким образом, для вычисления уравнения регрессии необходимо знать статистики системы случайных величин x и y. Качество регрессии, т.е. прогнозирования по уравнению регрессии, очевидно, тем выше, чем меньше сумма квадратов отклонений от линии регрессии
Анализ дисперсий можно представить таблицей
Пример. Исследовалась зависимость содержания меди y в рудном теле от расстояния от контакта x.
Вывод: существует значимая линейная зависимость содержания от расстояния. Величину среднеквадратической ошибки прогноза можно оценить также, используя коэффициент корреляции и общую дисперсию
Многомерная регрессия В этом случае находится зависимость выходной переменной Y от k входных переменных X. Уравнение (1) можно записать в матричном виде
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.007 с.) |

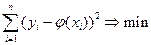 . Для линейной модели в случае одной переменной
. Для линейной модели в случае одной переменной 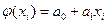 - называется также уравнением регрессии y на х. Регрессия y на х (рис. а)и х на y (рис. б).
- называется также уравнением регрессии y на х. Регрессия y на х (рис. а)и х на y (рис. б).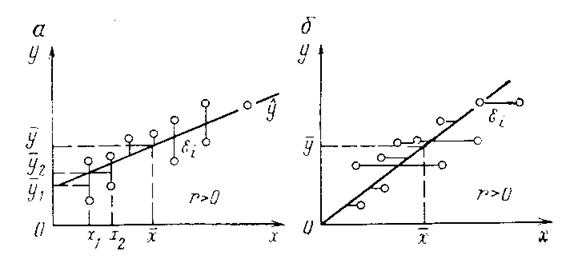
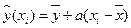 , (1)
, (1)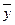 и
и 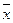 - соответственно средние значения выходной и входной переменных, a – коэффициент уравнения регрессии, который может быть выражен через оценки коэффициента корреляции rxy или ковариацию cov(x,y) и стандартs Sy, Sx
- соответственно средние значения выходной и входной переменных, a – коэффициент уравнения регрессии, который может быть выражен через оценки коэффициента корреляции rxy или ковариацию cov(x,y) и стандартs Sy, Sx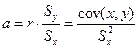 . (2)
. (2)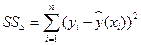 , что фактически означает: чем большую долю дисперсии выходной переменной объясняет линия регрессии, тем выше качество прогноза. Для оценки качества регрессии можно использовать схему дисперсионного анализа. Рассчитаем сумму квадратов отклонений уравнения регрессии от среднего выходной переменной
, что фактически означает: чем большую долю дисперсии выходной переменной объясняет линия регрессии, тем выше качество прогноза. Для оценки качества регрессии можно использовать схему дисперсионного анализа. Рассчитаем сумму квадратов отклонений уравнения регрессии от среднего выходной переменной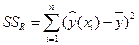 и общую дисперсию переменной y
и общую дисперсию переменной y 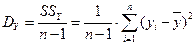 .
.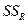

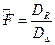
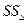
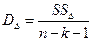
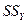
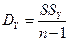
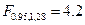
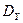
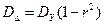 или для стандарта ошибки
или для стандарта ошибки 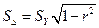 . В данном примере
. В данном примере 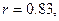
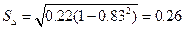
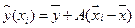 , где
, где 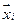 - вектор столбец (транспонированная i -я строка таблицы X). Вектор коэффициентов уравнения регрессии
- вектор столбец (транспонированная i -я строка таблицы X). Вектор коэффициентов уравнения регрессии 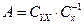 , где
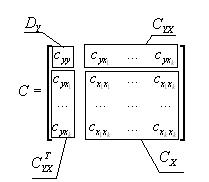
, где  - матрица взаимных ковариаций выходной и входных переменных;
- матрица взаимных ковариаций выходной и входных переменных; 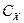 - ковариационная матрица входных переменных, которые могут быть легко сформированы из ковариационной матрицы
- ковариационная матрица входных переменных, которые могут быть легко сформированы из ковариационной матрицы 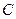 полной системы случайных величин, что показано в приводимых ниже матрице и на рис.
полной системы случайных величин, что показано в приводимых ниже матрице и на рис.