
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая обработка одномерных количественных данных.Содержание книги
Поиск на нашем сайте
Выборка из генеральной совокупности Статистика - любая функция выборки случайной величины Например, среднее арифметическое значение
или среднеквадратическое отклонение (оценка стандартного отклонения или стандарт).
Статистики являются функциями случайных величин – выборочных значений и, поэтому их распределение может быть описано некоторым законом распределения. Например, в соответствии с центральными предельными теоремами ТВ, среднее значение случайной величины, распределенной по любому закону, будет близко к нормальному, если для вычисления среднего используется более 15-20 значений.
Аналоги числовых характеристик случайных величин – одномерные статистики:
В качестве робастной оценки (устойчивой к «ураганным» выбросам) – медиана – значение, которое делит выборку пополам
В качестве робастной оценки разброса используется медианное отклонение
Гистограмма – аналог плотности вероятностей. Гистограмма характеризует распределение числа объектов, попавших в интервалы. Для определения числа интервалов можно использовать различные правила (формула Стреджесса и пр.). Самое простое – число интервалов оценивать как корень квадратный из объема выборки. Объем выборки для построения гистограмм должен быть не менее 40-50 объектов.
Из гистограммы можно получить экспериментальный аналог плотности вероятностей и, наоборот, зная плотность вероятности (плотность) можно получить теоретическую гистограмму. Зная число объектов ni, попавших в i -й интервал длиной Δx, а также объем выборки N, для этого интервала оцениваем вероятность попадания pi = ni/N, а затем значение экспериментальной плотности di = pi/ Δx. Для определения теоретического значения числа объектов ΔNi, попавших в i -й интервал, необходимо найти вероятность попадания в этот интервал Δ Pi по принятой модели плотности распределения f(x):
В Mathcad – для построения гистограмм можно использовать функции hist и histogram.
Непараметрические статистики: медиана, медианное отклонение, вариационный ряд, ранги значений и их вычисление.
Проверка гипотезы о законе распределения по критерию χ2 Гистограмма – распределение вероятностей попадания в интервалы значений случайной величины. Гистограмма м.б. теоретическая – ее вычисляют, опираясь на модель распределения и эмпирическая, полученная в результате обработки опытных данных. Для построения эмпирической гистограммы необходимо определить число интервалов. Самое простое правило – число интервалов оценивать как корень квадратный из объема выборки. Объем выборки для построения гистограмм должен быть не менее 40-50 объектов. Теоретическую гистограмму можно рассчитать, зная параметры распределения, например, нормальное распределение … Критерий
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.66.147 (0.008 с.) |

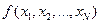 или
или  , где
, где 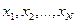 - выборочные значения из некоторой генеральной совокупности значений.
- выборочные значения из некоторой генеральной совокупности значений.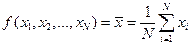
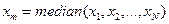 . (3)
. (3)
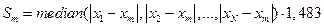 . (4)
. (4)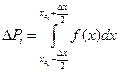 , где
, где 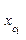 - центр i-го интервала, а затем вычислить ΔNi = Δ PiN.
- центр i-го интервала, а затем вычислить ΔNi = Δ PiN.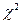 позволяет количественно оценить сходство эмпирического распределения с теоретическим.
позволяет количественно оценить сходство эмпирического распределения с теоретическим.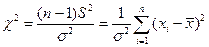 имеет
имеет 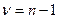 .
.



