Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геолого-геофизические приложения регрессионного анализаСодержание книги
Поиск на нашем сайте
Использованием аппарата регрессионного анализа для решения задачи прогноза значений некоторой переменной по значениям других переменных открывает широкие горизонты практических приложений. 1. Прогноз значений физических характеристик (плотности по магнитной восприимчивости, удельному электрическому сопротивлению и т.п.; прогноз запасов в месторождении по значениям физических полей и данным геохимического опробования и т.п.). Одни свойств измерены, например, по каротажным данным, а другие надо установить для дальнейшего использования при интерпретации данных. Например, при решении обратной задачи установить пределы возможных изменений плотности и т.п. 2. Интерполяция и экстраполяция - заполнение в таблице недостающих данных. Т.е. «дырки» в таблице заполнять с помощью уравнений регрессии. Причем это касается не только нескольких переменных, но также по одному методу. Например, в таблице данных магнитной съемки по техническим причинам отсутствуют значения на некоторых профилях. Показать, как можно сформировать уравнения регрессии для решения задач интерполяции и экстраполяции. Метод главных компонент (МГК) Principal Components Method (PCM), Principal Components Analysis (PCA)
МГК является мощным инструментом анализа многомерных данных и позволяет:
Главными компонентами (ГК) называются линейные комбинации исходных признаков, проходящие вдоль главных осей эллипсоида рассеивания. ГК ортогональны между собой, что равносильно их некоррелированности в рамках модели многомерного нормального распределения. Пусть имеется исходная таблица Х, состоящая из m колонок и n строк. Придерживаясь модели нормального распределения, эти данные можно представить в m -мерном пространстве признаков в виде рассеяния точек в объеме m -мерного эллипсоида. Проекции на оси этого эллипсоида называются главными компонентами выборки Х.
Коэффициенты в уравнениях главных компонент t1,…tp можно определить по ковариационной матрице С, которую можно представить разложением по собственным значениям и векторам:
Каждый i -й столбец матрицы V соответствует собственному значению λ i
Если p = m, то в выражении (1) соблюдается точное равенство, т.к V = Vp. Если же p < m, то новая матрица Cp
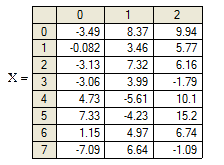
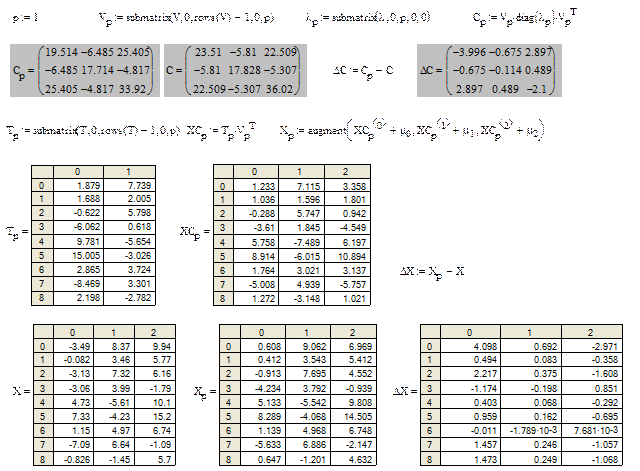
Пусть дана табл. X с m = 3 столбцами, рассчитаем по программе StatM статистики:
Составим функцию для расчета собственных значений и собственных векторов ковариационной матрицы. Также в ней вычисляется относительный вклад d главных компонент в общую дисперсию системы признаков, которая равна следу матрицы C – tr(c) - сумма элементов главной диагонали, на которой стоят, как известно дисперсии признаков.
Легко проверить правильность разложения по базису собственных векторов
, т.е. получается исходная ковариационная матрица C. Составляющие собственного вектора – это направляющие косинусы соответствующей главной оси эллипсоида. Поэтому сумма квадратов элементов в каждом столбце матрицы V равна 1:
Спроектируем данные на оси ГК, перенося с помощью операции центрирования начало новой системы координат в центр эллипсоида
Ниже показана выборка в осях исходных признаков и осях главных компонент T. По величине d видно, что первые две главные компоненты исчерпывают 92% общей дисперсии выборки. Поэтому можно без особых потерь информации основные особенности трехмерной выборки отразить в двумерном пространстве первых двух главных компонент
Аналогичное разложение можно провести для корреляционной матрицы
Гл. 3. Принципы формирования стохастических моделей системы "объект-поле"
Построение моделей, отражающих особенности распределения гравитационного поля над средой с хаотическим распределением плотностных неоднородностей, увеличивает разнообразие математических моделей, использующихся в теории и практике интерпретации потенциальных полей. Расчет вероятностных законов распределения гравитационного поля на основе математических моделей случайно-неоднородных сред является дальнейшим развитием способов стохастического моделирования геологических объектов сложного строения, позволяющих рассчитывать количественные характеристики стохастической системы «сложный объект-поле» [Вахромеев, Давыденко,1987]. Возможности вероятностно-статистического подхода могут быть расширены за счет развития способов прямого расчета вероятностных распределений для стохастических моделей неоднородных объектов. Постановка задачи Предположим, что в некотором объеме геологической среды случайным образом распределены неоднородности. Понятие «случайным образом» означает, что фактическая совокупность неоднородностей в моделируемом геологическом объекте рассматривается как частная реализация из множества возможных реализаций генеральной совокупности системы «сложный объект-поле». Параметры такой генеральной совокупности определены свойствами и особенностями пространственного распределения физико-геологических неоднородностей, то есть характеристиками стохастической модели объекта. Известные способы решения прямой задачи в стохастической постановке позволяют рассчитывать для модели системы «сложный объект-поле» функции математического ожидания и дисперсии, а также авто- и взаимные корреляционные функции случайных полей и параметров модели сложного объекта [Вахромеев, Давыденко, 1987; Vakhromeyev G.S, Davydenko A.Yu., 1987, 1989]. Развитие стохастического подхода в геолого-геофизических приложениях приводит к необходимости разработки аппарата для расчета более полных характеристик системы «сложный объект-поле». В этом отношении существенный теоретический и практический интерес, особенно для статистических методов анализа и интерпретации геофизических полей, имеет решение прямой задачи для функции и плотности вероятности стохастического аномального эффекта. Знание или, по крайней мере, оценка законов распределения случайных полей, обусловленных суммарным эффектом случайных неоднородностей, позволяет обосновать применимость того или иного способа выделения слабых сигналов на фоне случайных помех [Никитин, 1986; Вахромеев, Давыденко,1987], оценить корректность конкретного способа решения обратной задачи. Важной является также возможность моделируемых и эмпирических законов распределения случайных полей с позиций геолого-геофизической информации об особенностях неоднородного строения генерирующих эти поля сложных объектов. Стохастическая модель Представим аномальный эффект U в точке x суперпозицией аномальных эффектов m неоднородностей:
В общем случае число неоднородностей m является дискретной случайной величиной, распределение которой зависит от принятой модели случайного распределения неоднородностей в объеме моделируемого объекта. Следует также отметить, что каждое отдельное слагаемое в (1) также может представлять суммарный эффект неоднородностей некоторой генеральной совокупности. Различия в вероятностных характеристиках таких генеральных совокупностей обусловлены различными физико-геологическими параметрами типов неоднородностей, представленных в стохастической модели. Так, например, серия рудных жил в пределах некоторой рудной зоны может быть аппроксимирована случайным расположением в пространстве тонких пластин, а неоднородности в толще четвертичных отложений или вмещающих породах – в виде случайного пуассоновского поля точечных источников. Обычный недостаток существенной априорной геолого-геофизической информации вполне оправдывает допустимость фактической независимости случайных физико-геометрических характеристик различных типов неоднородностей, а это означает возможность декомпозиции суммы (1) на независимые подсуммы, соответствующие типам неоднородностей. Таким образом, в случае необходимости усложнения модели i-е слагаемое в (1) можно рассматривать как суммарный эффект случайных неоднородностей i-го типа с заданными вероятностными характеристиками. Поэтому без существенного ограничения общности последующих выводов будем полагать, что (1) выражает суммарный эффект неоднородностей только одного типа генеральной совокупности, причем случайные характеристики различных неоднородностей являются независимыми и неразличимыми в статистическом смысле. Прямая задача в вероятностно-статистической постановке Принятая модель позволяет определить функцию F(U) и плотность f(U) распределения аномального эффекта по известным формулам для вероятностной смеси распределений независимых случайных величин [Вентцель, Овчаров, 1988]:
где p1, p2, …, pn; Учитывая принятые для модели допущение о независимости случайных параметров различных неоднородностей, можно определить функцию и плотность распределения суммы j независимых случайных величин через операцию j-кратной свертки [Корн Г., Корн Т., 1973]:
где, в соответствии со статистической неразличимостью (одинаковым распределением) параметров различных неоднородностей,
Таким образом, для нахождения функции (2) и плотности распределения (3) необходимо знать функцию и/или плотность распределения эффекта одиночной неоднородности и задать модель случайного распределения этих неоднородностей в объеме моделируемого объекта. В гравимагниторазведке стохастический аномальный эффект одиночной неоднородности обычно можно представить в виде
где Если предположить независимость амплитудных и геометрических случайных параметров для отдельной неоднородности и обозначить соответствующие плотности распределений
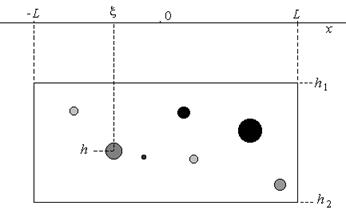
Интегрирование выражения (6) в пределах от -¥ до u позволяет также определить функцию распределения Для определения плотности смеси распределений (3) необходимо задать ряд распределения числа неоднородностей - вероятности p1, p2, …, pn. Эти вероятности можно определить на основе модели случайного распределения источников в объеме моделируемого объекта. Пример Рассмотрим расчета параметров вероятностных распределений составляющей Vz гравитационного поля для случайно-неоднородной среды, представленной ансамблем неоднородностей в виде горизонтальных материальных нитей со случайной массой и случайным распределением в объеме двумерной горизонтальной призмы прямоугольного сечения (рис.1).
Рис. 1. Геометрические параметры модели случайно-неоднородной горизонтальной прямоугольной призмы.
Будем полагать, что число неоднородностей, попадающих в контур призмы, подчиняется распределению Пуассона. В этом случае, если известен параметр l - среднее число случайных источников на единицу площади разреза, то вероятности в (2) и (3) где a= lS – математическое ожидание числа неоднородностей в контуре, ограничивающем площадь S (в нашем случае S = 2L(h2 –h1)).
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.227.250 (0.007 с.) |

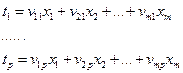
 . (1)
. (1)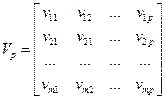 ,
, 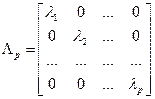 .
.
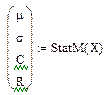
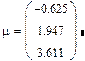
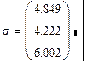
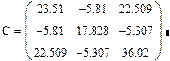


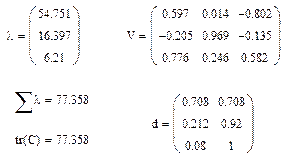

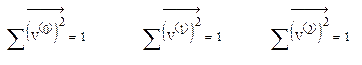 .
.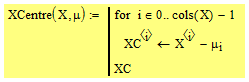
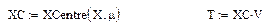
 . По этим компонентам можно приближенно восстановить не только ковариационную матрицу при значении p =2, но также приближенные значения исходной трехмерной системы признаков Xp.
. По этим компонентам можно приближенно восстановить не только ковариационную матрицу при значении p =2, но также приближенные значения исходной трехмерной системы признаков Xp.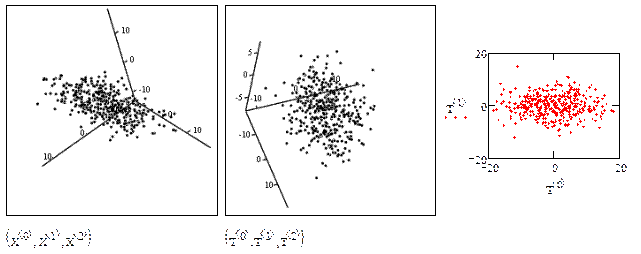
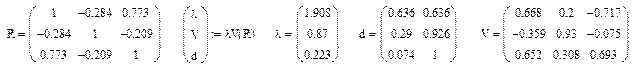
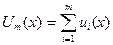 . (1)
. (1)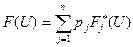 , (2)
, (2)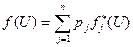 , (3)
, (3)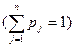 - ряд распределения, характеризующий вероятности появления соответственно 1, 2, … n неоднородностей в объеме модели, а
- ряд распределения, характеризующий вероятности появления соответственно 1, 2, … n неоднородностей в объеме модели, а 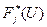 и
и 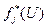 - соответственно функция и плотность распределения для суммарного эффекта с j слагаемыми.
- соответственно функция и плотность распределения для суммарного эффекта с j слагаемыми.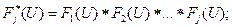
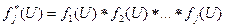 , (4)
, (4)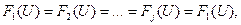
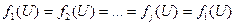 .
.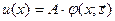 или
или 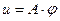 , (5)
, (5)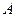 - случайный амплитудный фактор, зависящий от случайных параметров массы неоднородности;
- случайный амплитудный фактор, зависящий от случайных параметров массы неоднородности; 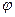 - координатная функция, являющаяся случайной величиной в силу случайности вектора геометрических параметров (форма и положение неоднородности)
- координатная функция, являющаяся случайной величиной в силу случайности вектора геометрических параметров (форма и положение неоднородности) 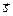 .
.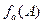 и
и 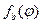 , то на основе известного в теории вероятностей правила [Вентцель, Овчаров, 1988] плотность распределения случайного аномального эффекта одиночной неоднородности (5) можно записать в виде
, то на основе известного в теории вероятностей правила [Вентцель, Овчаров, 1988] плотность распределения случайного аномального эффекта одиночной неоднородности (5) можно записать в виде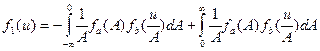 . (6)
. (6)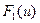 .
.
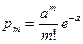 , (7)
, (7)