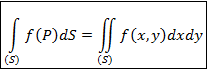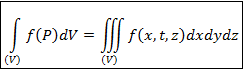Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение функции, заданной на отрезке в ряд Фурье
Если функция продолжена четным образом Если нечетным
Ряды Фурье в комплексной форме
Спектральные характеристики периодической функции -свойство линейности - свойство дифференцирования -свойство интегрирования -спектр смещенной функции -изменение масштаба Интегралы по фигуре Понятие фигуры, её диаметра, меры. Вычисление массы фигуры. Понятие интеграла по фигуре, его свойства и приложения. “фигура” – отрезок Мерой одномерной фигуры длина, мерой двумерной фигуры площадь, мерой трехмерной фигуры объем. Назовем диаметром Вычисление массы фигуры
Понятие интеграла по фигуре
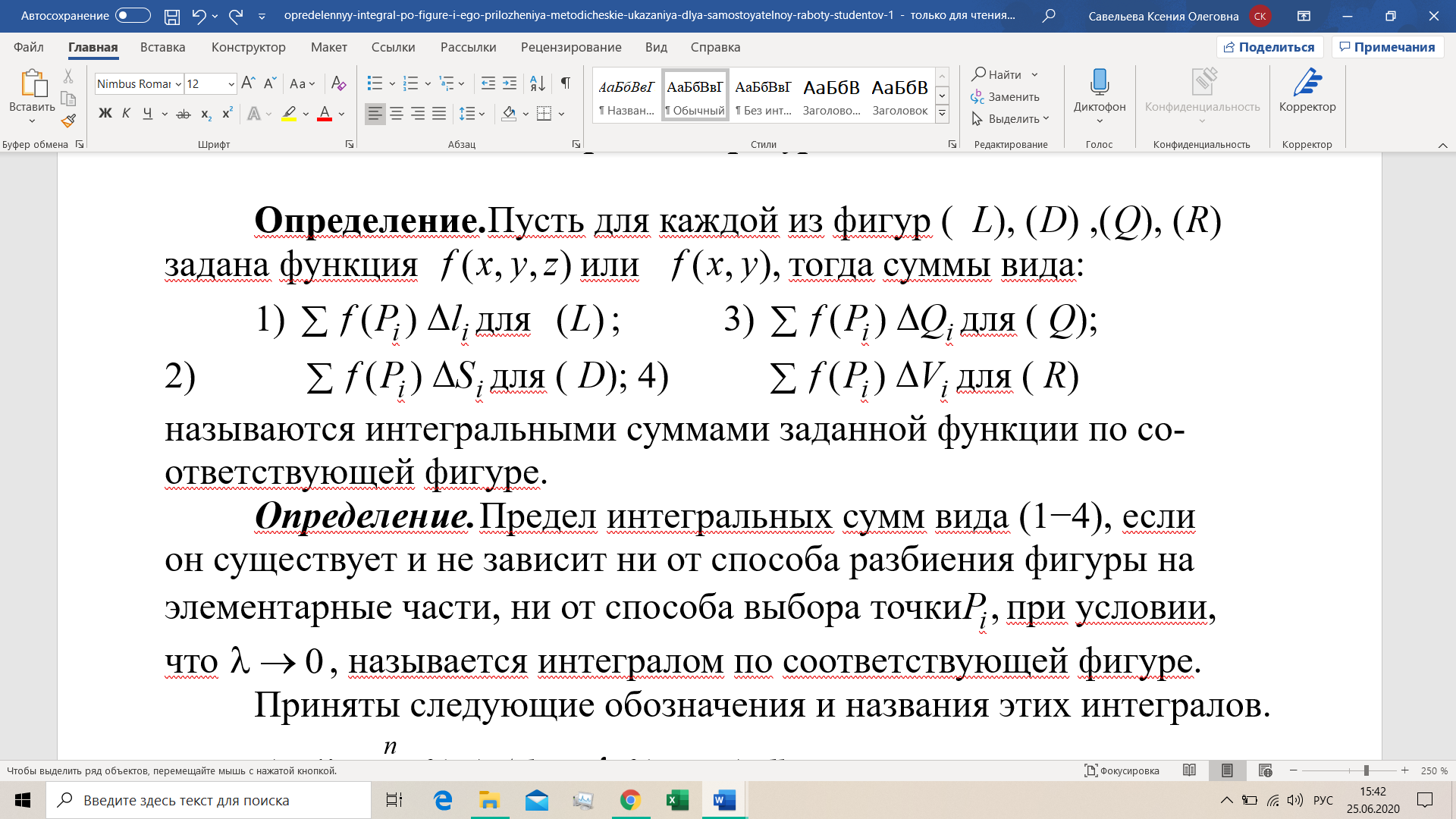
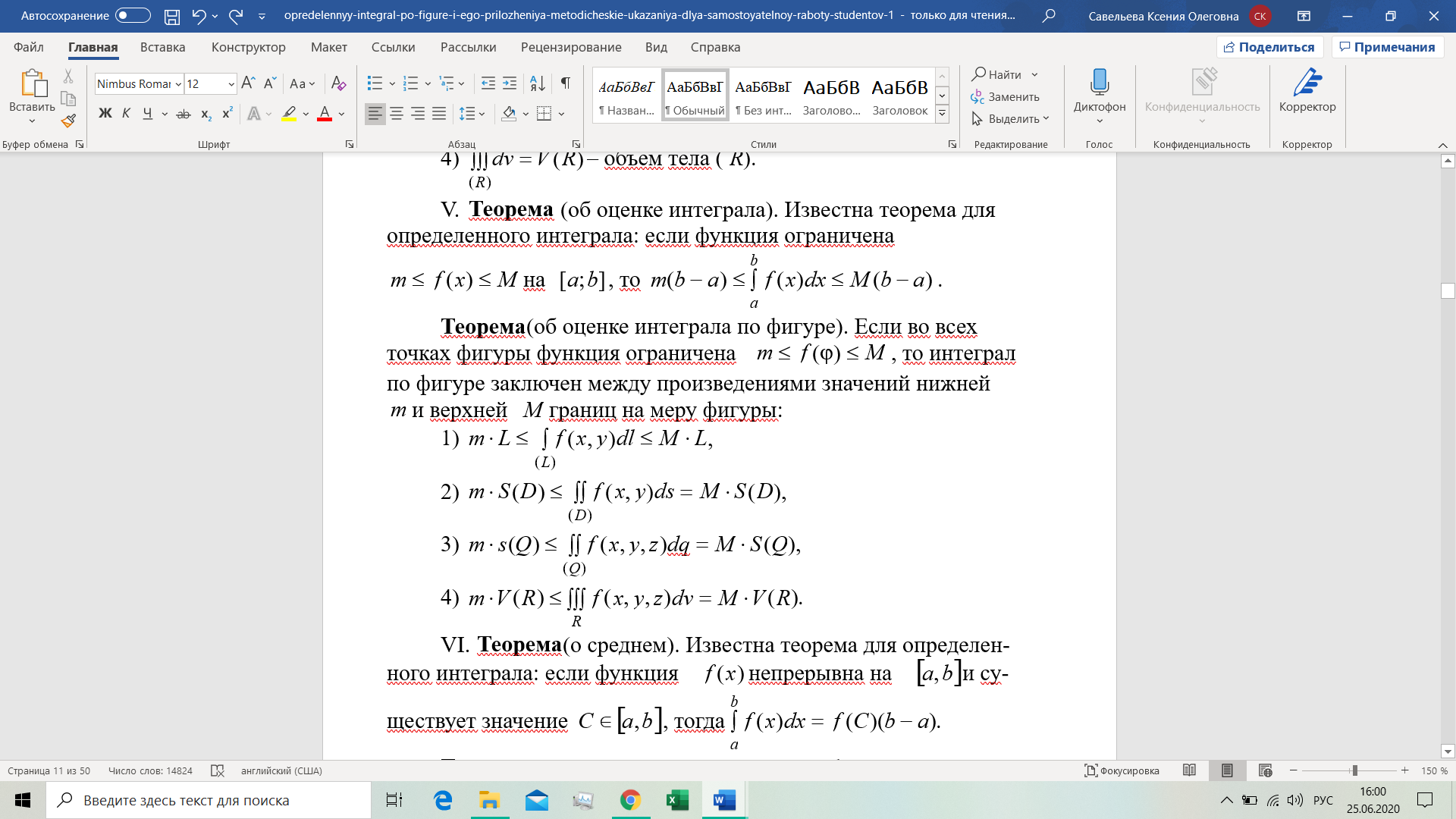
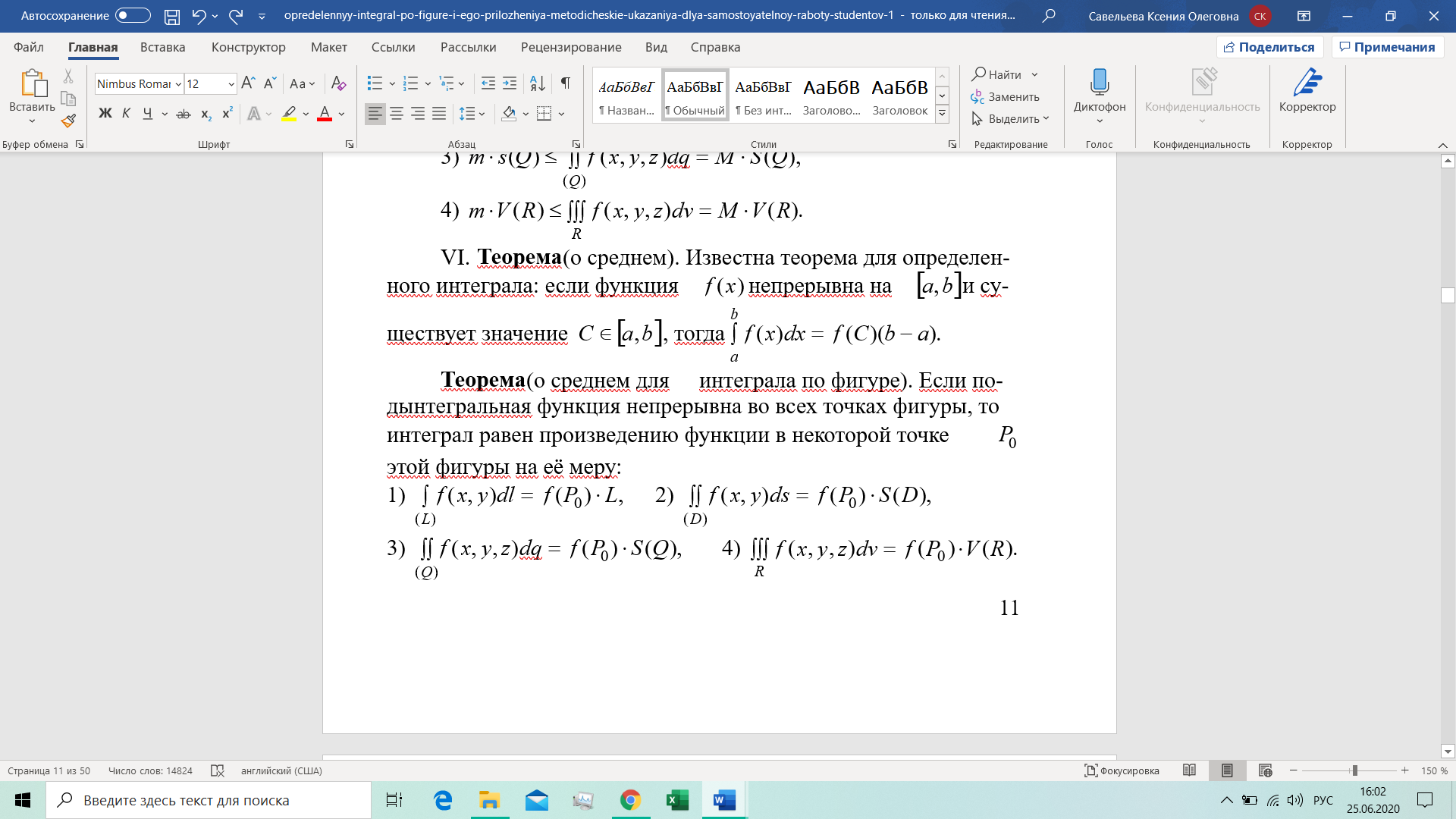
Лямда – диаметр фигуры. Свойства интеграла по фигуре: · Интеграл от суммы функций равен сумме интегралов. Выполняется при условии, что обе функции интегрируемы · Вынесение константы за знак интеграла · Разбие области на части соответсвует сумме интегралов · Если подынтегральная функция равна 1, то интеграл по фигуре численно равен мере фигуры
Приложения интеграла по фигуре
Конкретные виды интеграла по фигуре: криволинейный, двойной, тройной, Поверхностный. Мы рассматривали фигуры пяти видов: отрезок, дугу кривой, поверхность, плоскую область и тело. Следовательно, мы получим пять видов интегралов по фигуре:
1. Если фигура (Ф) является отрезком [a,b], то интеграл называют определенным интегралом и обозначают
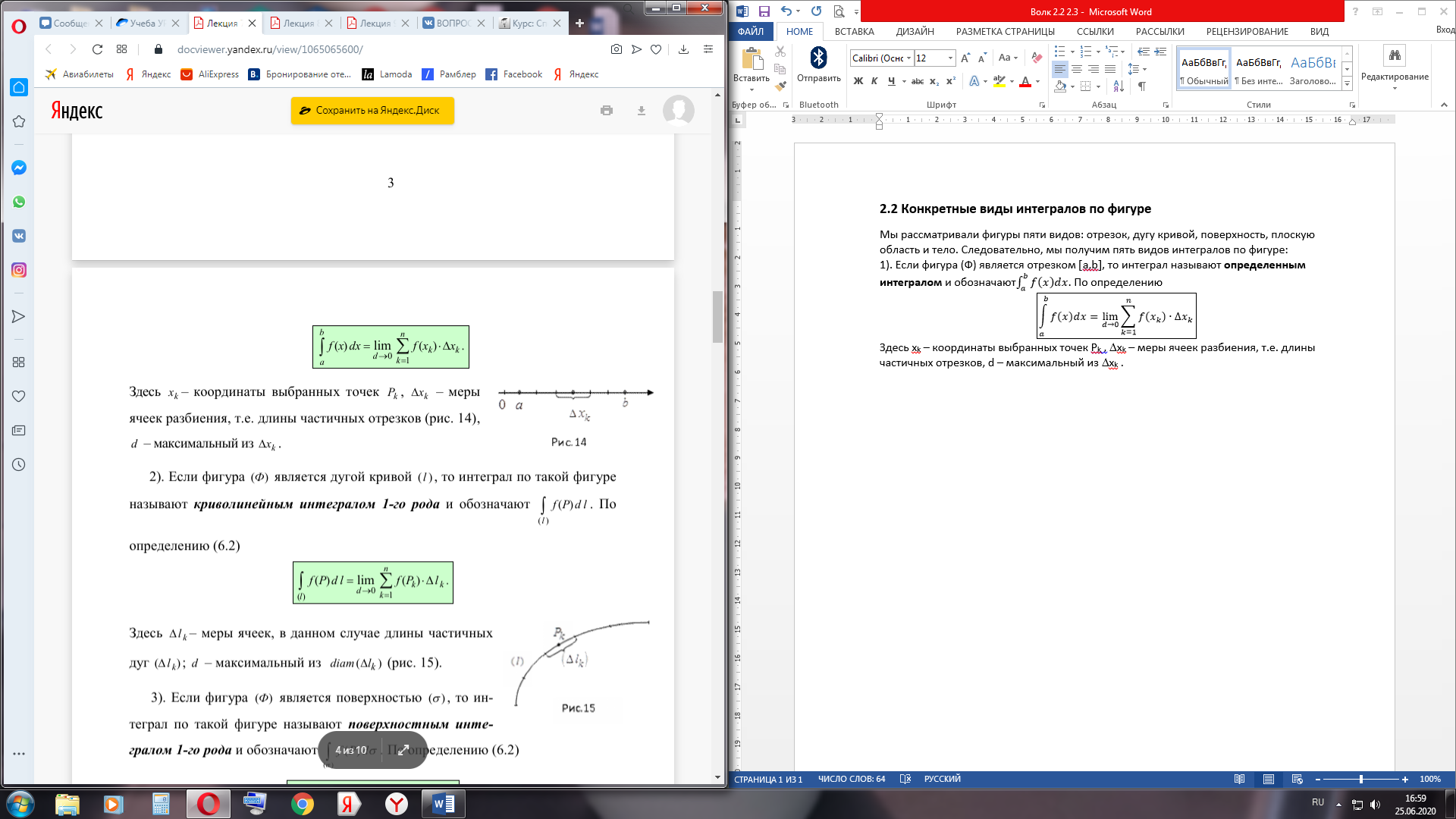
2. Если фигура (Ф) является дугой кривой (l), то интеграл по такой фигуре называют криволинейным интегралом 1-го рода и обозначают
Здесь Dlk – меры ячеек, в данном случае длины частичных дуг (Dlk); d – максимальный из diam (Dlk).
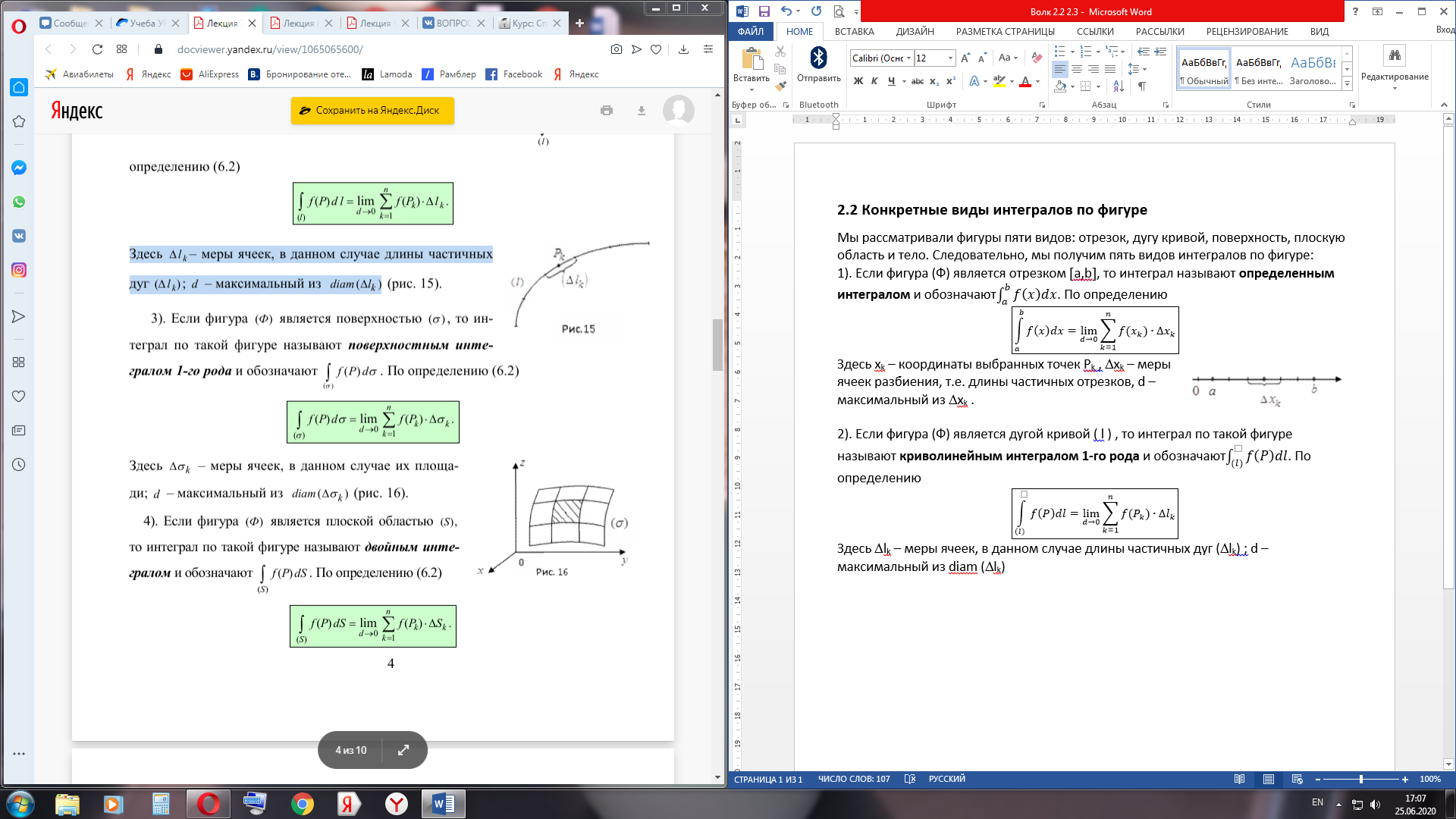
3. Если фигура (Ф) является поверхностью (s), то интеграл по такой фигуре называют поверхностным интегралом 1-го рода и обозначают
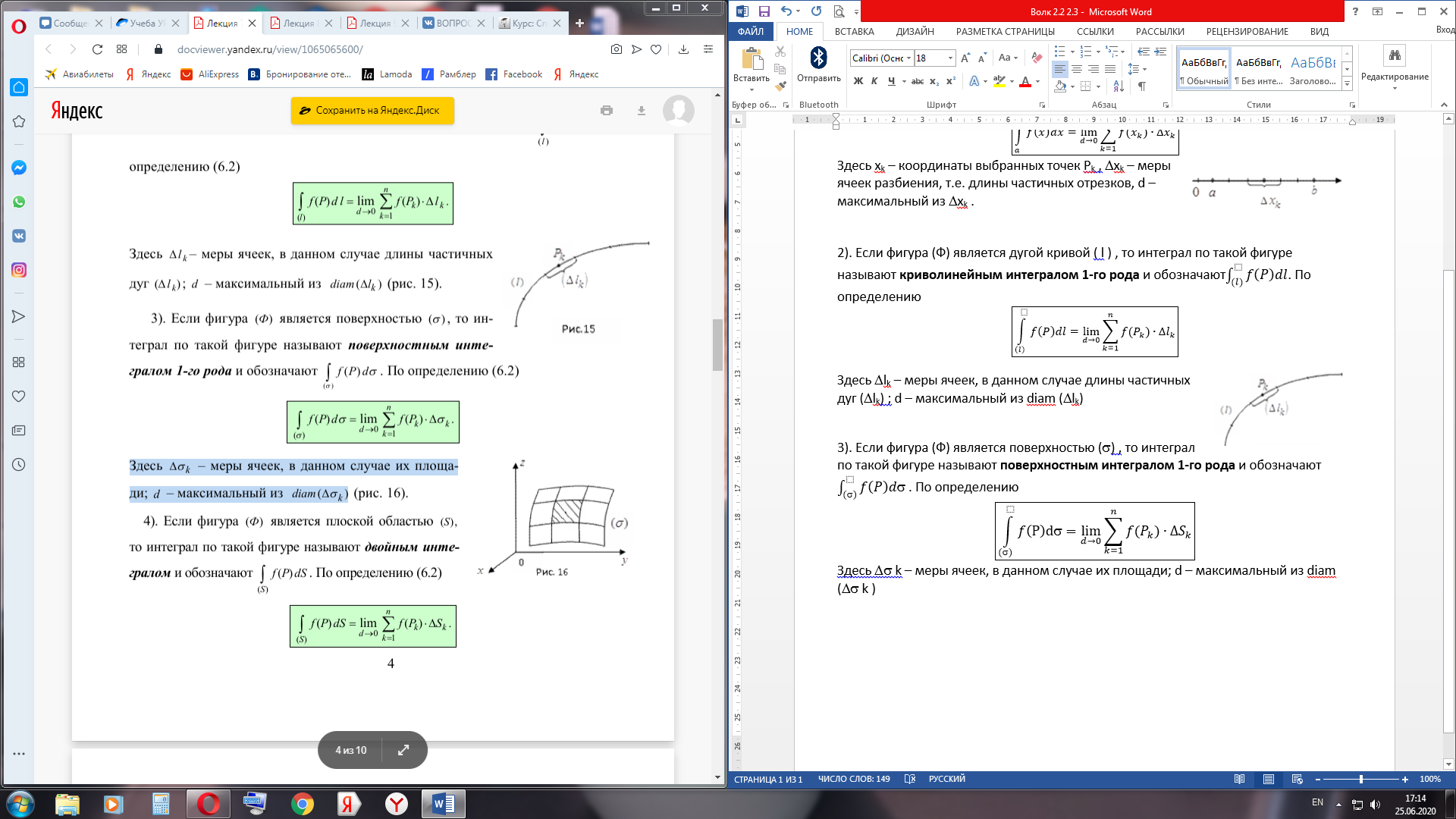
4. Если фигура (Ф) является плоской областью (S), то интеграл по такой фигуре называют двойным интегралом и обозначают
5. Если фигура (Ф) является телом (V), то интеграл по такой фигуре называют тройным интегралом и обозначают
dS = dx × dy,
Аналогичная форма записи принята и для тройного интеграла
|
|||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.69.45 (0.012 с.) |
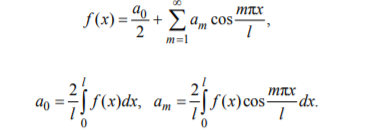
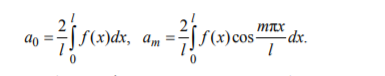

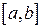 , дугу
, дугу 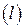 , плоскую область
, плоскую область 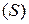 , поверхность
, поверхность  , тело
, тело  . Отрезок и дугу назовем одномерной фигурой, плоскую область и поверхность – двумерной фигурой, тело – трехмерной фигурой.
. Отрезок и дугу назовем одномерной фигурой, плоскую область и поверхность – двумерной фигурой, тело – трехмерной фигурой.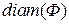 фигуры
фигуры  наибольшее из расстояний между ее точками
наибольшее из расстояний между ее точками

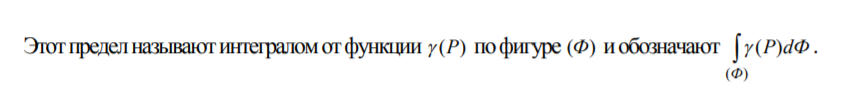



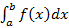 . По определению
. По определению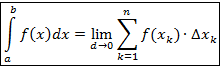
 Здесь xk – координаты выбранных точек Pk, Dxk – меры ячеек разбиения, т.е. длины частичных отрезков, d – максимальный из Dxk.
Здесь xk – координаты выбранных точек Pk, Dxk – меры ячеек разбиения, т.е. длины частичных отрезков, d – максимальный из Dxk.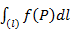 . По определению
. По определению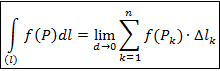
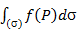 . По определению
. По определению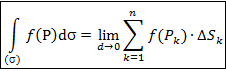
 Здесь Dsk – меры ячеек, в данном случае их площади; d – максимальный из diam (Dsk).
Здесь Dsk – меры ячеек, в данном случае их площади; d – максимальный из diam (Dsk).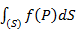 . По определению
. По определению
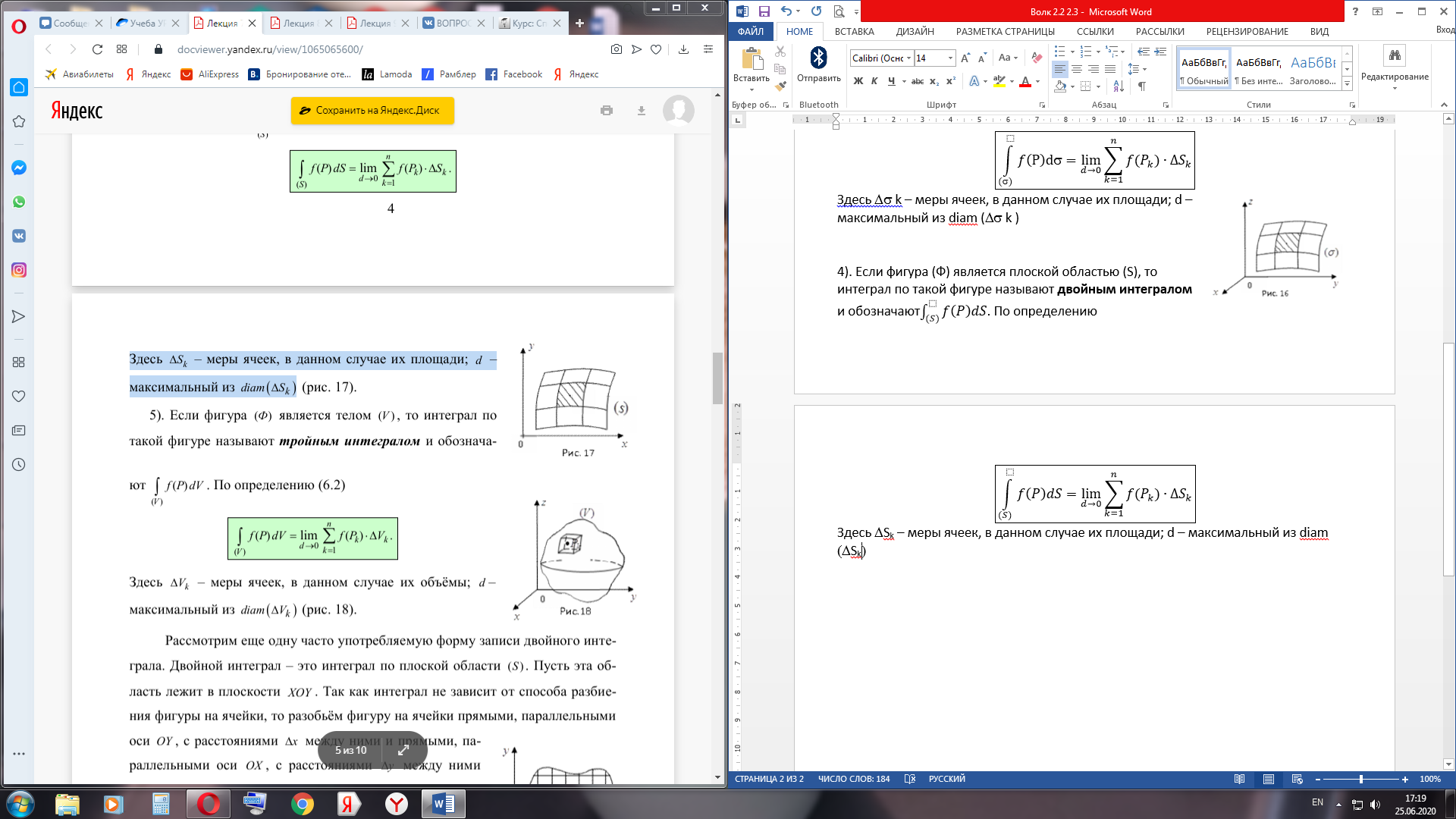 Здесь DSk – меры ячеек, в данном случае их площади; d – максимальный из diam (DSk).
Здесь DSk – меры ячеек, в данном случае их площади; d – максимальный из diam (DSk).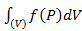 . По определению
. По определению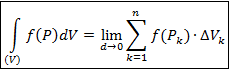
 Здесь DVk – меры ячеек, в данном случае их объёмы; d – максимальный из diam (DVk).
Здесь DVk – меры ячеек, в данном случае их объёмы; d – максимальный из diam (DVk). Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области (S). Пусть эта область лежит в плоскости XOY. Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьём фигуру на ячейки прямыми, параллельными оси OY, с расстояниями Dx между ними и прямыми, параллельными оси OX, с расстояниями Dy между ними (рис. 19). Тогда площадь любой ячейки, кроме приграничной, равна DS = Dx × Dy. Поэтому dS и интеграл записывают в следующем виде:
Рассмотрим еще одну часто употребляемую форму записи двойного интеграла. Двойной интеграл – это интеграл по плоской области (S). Пусть эта область лежит в плоскости XOY. Так как интеграл не зависит от способа разбиения фигуры на ячейки, то разобьём фигуру на ячейки прямыми, параллельными оси OY, с расстояниями Dx между ними и прямыми, параллельными оси OX, с расстояниями Dy между ними (рис. 19). Тогда площадь любой ячейки, кроме приграничной, равна DS = Dx × Dy. Поэтому dS и интеграл записывают в следующем виде: