
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и условная сходимостьСодержание книги Поиск на нашем сайте
Знакопеременный ряд
Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин расходится, то ряд называется условно сходящимся.
Комплексные числовые ряды Числовым рядом с комплексными членами называется ряд
Где Сn=an + ibn, a и b – действительные числа.
1.2 Степенные ряды Степенным рядом называется функциональный ряд вида
или вида
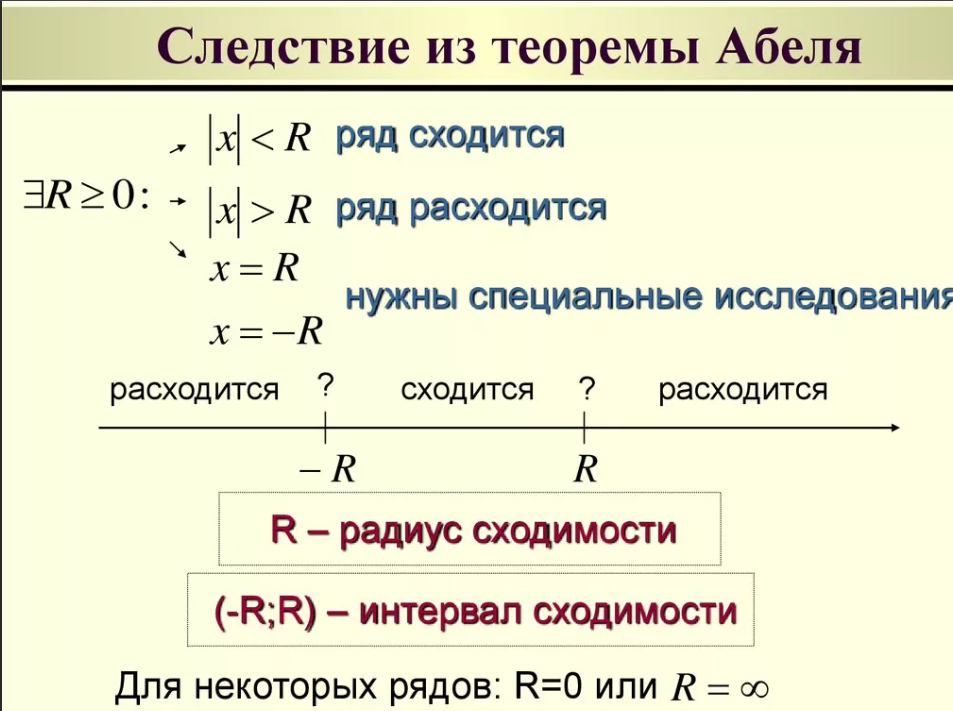
где x0, a0, a1, a2,... — действительные числа. Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема Абеля 1) Если степенной ряд сходится при 2) Если ряд расходится при некотором значении х0', то он расходится при всяком x, для которого
Свойства степенных рядов Пусть дан некоторый степенной ряд (1) 1) Сумма степенного ряда (1) есть функция непрерывная во всех внутренних точках интервалов сходимости ряда 2) Степенной ряд (1) можно почленно интегрировать если пределы интегрирования являются внутренними точками интервала сходимости ряда. 3) Если степенной ряд (1) почленно проинтегрировать на отрезке (-R; R) [0;х] |x|<R, то полученный степенной ряд будет иметь тот же радиус сходимости R, что и степенной ряд (1). 4) Степенной ряд (1) внутри его интервала сходимости можно почленно дифференцировать сколь угодно раз. Получаем, что степенные ряды имеют тот же радиус сходимости R, что и ряд (1). Ряды Тейлора и их применение к вычислению Значений функции, к вычислению определенных интегралов, к решению Дифференциальных уравнений. Пусть f (x) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков, тогда степенной ряд Называется рядом Тейлора функции f(x) в точке x0 В случае x0 = 0 ряд называется рядом Маклорена в точке x0=0
Применение ряда Тейлора к вычислению Значений функции
Применение ряда Тейлора к вычислению определенных интегралов
При вычислении определенных интегралов мы можем воспользоваться стандартными разложениями функций. Члены ряда отбрасывают учитывая погрешность вычисления.
Разложение периодической функции в тригонометрический ряд Фурье. Ряд Фурье для четной и нечетной функции. Разложение функции, заданной на отрезке в ряд Фурье. Ряд Фурье в комплексной форме. Спектральные характеристики периодической функции. Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+..., где ao, a1,a2,...,b1,b2,.. - действительные константы, т.е.
Ряд Фурье для четной и нечетной функции
|
|||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.103 (0.009 с.) |

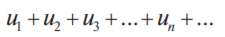
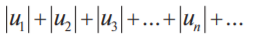
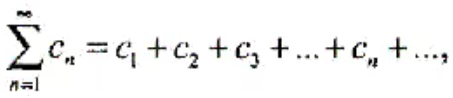

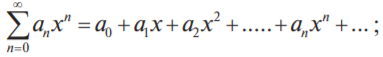
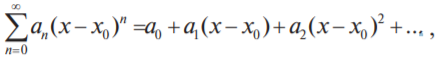
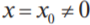 , то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству 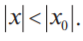
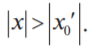
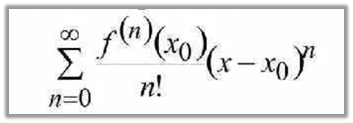
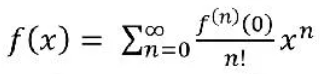


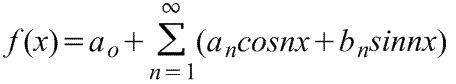 (1)
(1)



