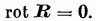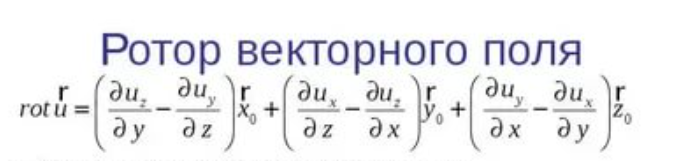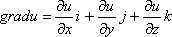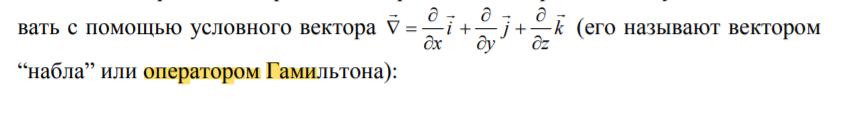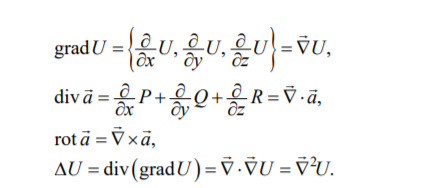Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные свойства дивергенциСодержание книги Поиск на нашем сайте
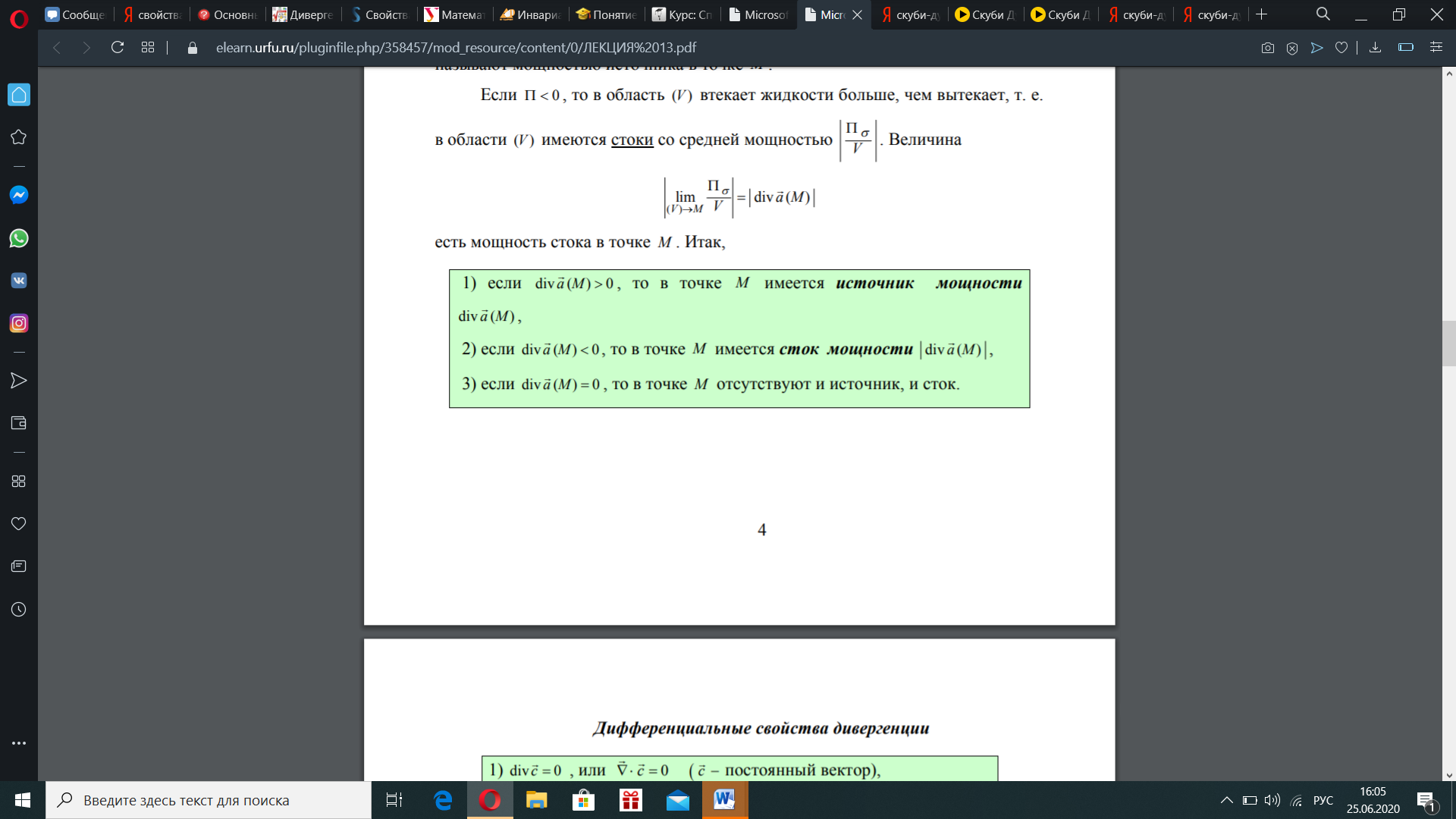
В каждой точке М поля А показывает наличие источников или стоков поля:
Линейный интеграл поля и свойства линейного интеграла. Циркуляция
В тех случаях, когда линейный интеграл поля a r берется по замкнутой кривой L, он называется Вычисление линейного интеграла
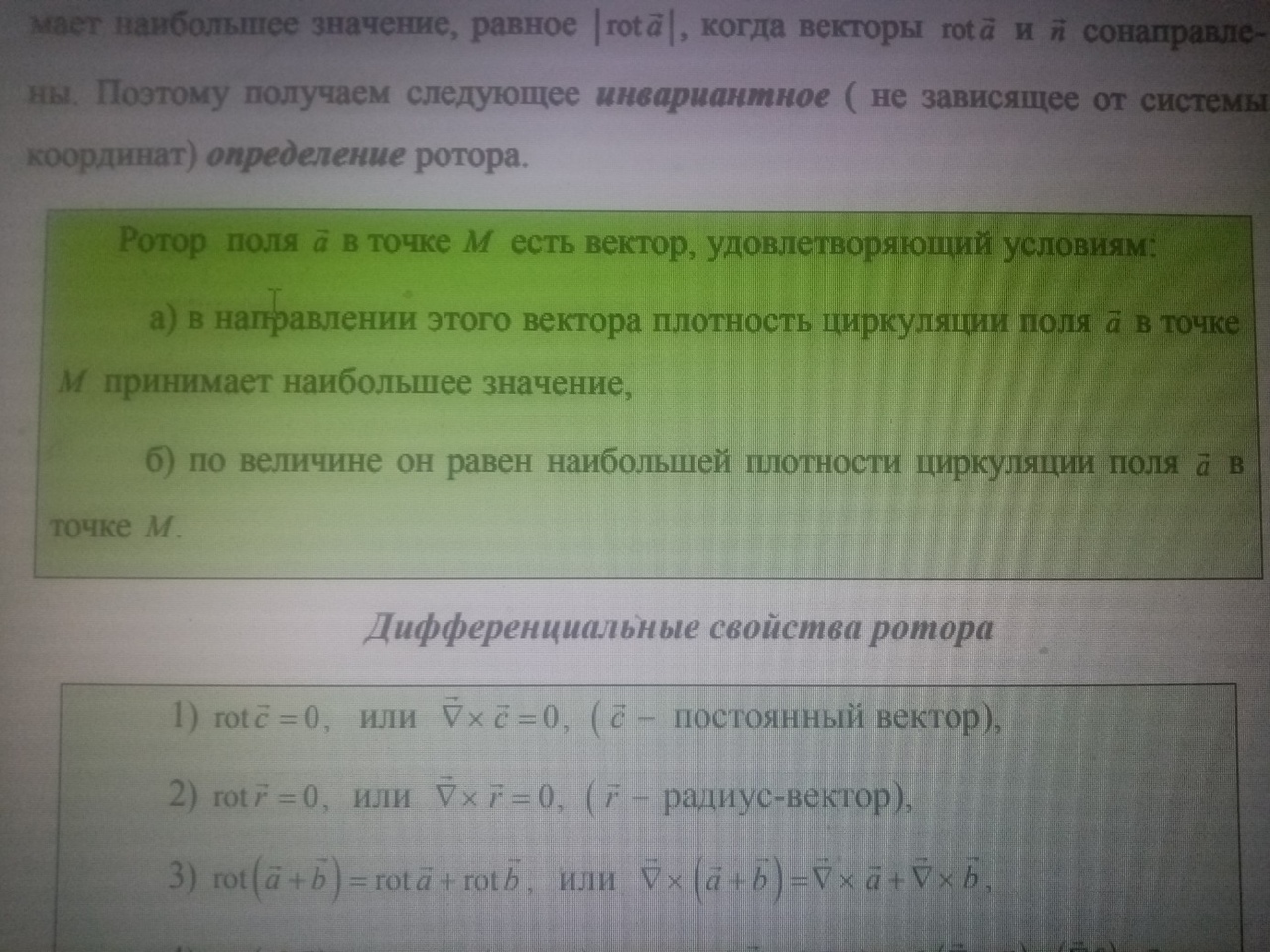
Понятие Ротора: Физический смысл ротора: Таким образом, ротор поля линейных скоростей в любой точке равен удвоенному вектору угловой скорости. В произвольном поле его ротор, вычисленный в точке M, также характеризует вращательную способность поля в этой точке. Инвариантное определение ротора:
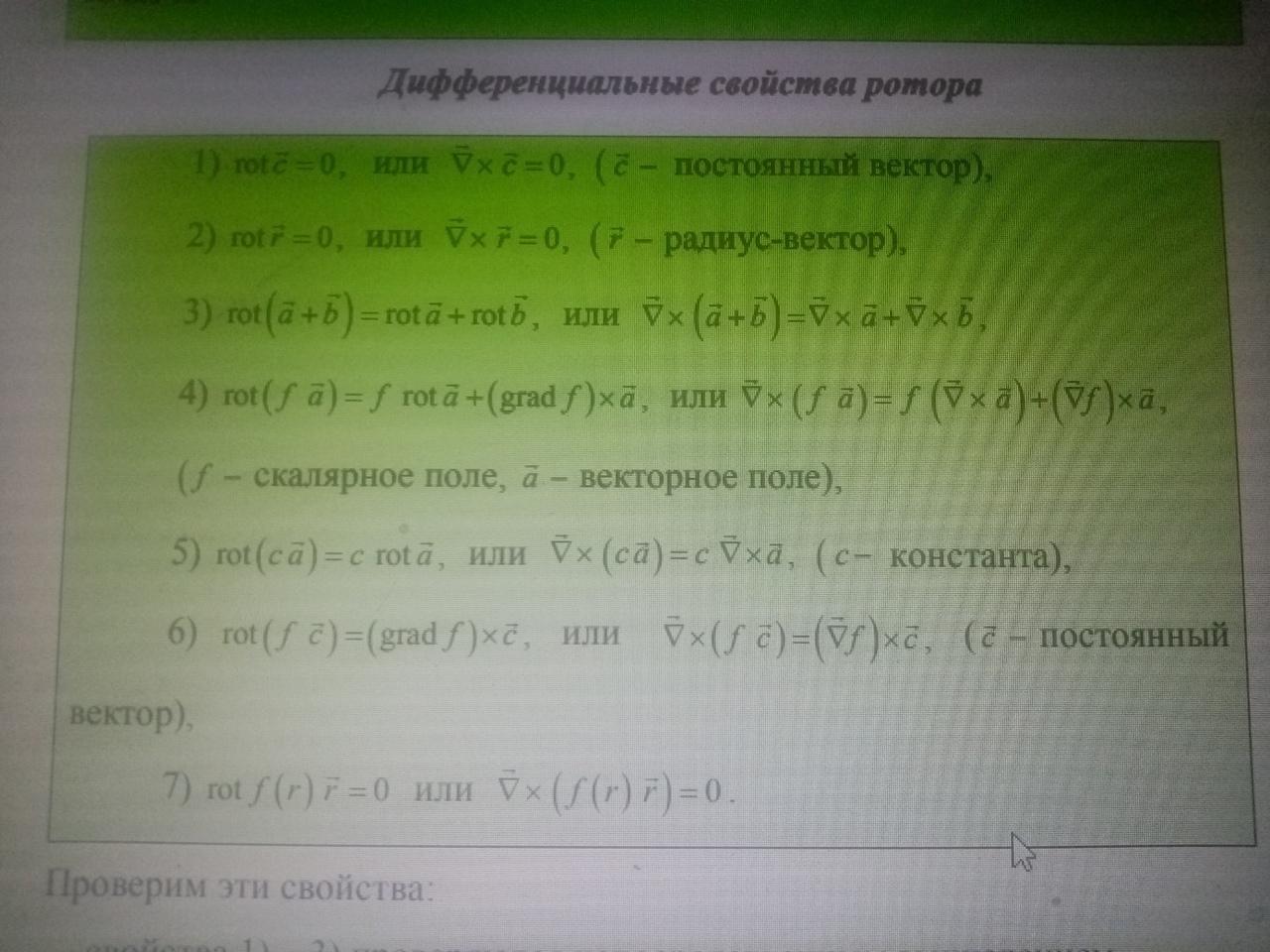
Дифференциальные свойства ротора:
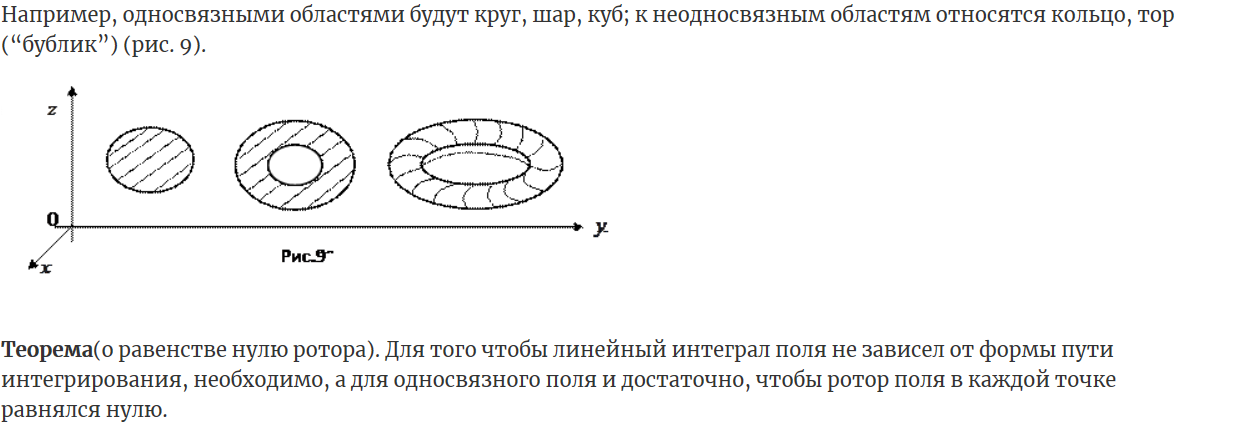
Условие независимости линейного интеграла поля от формы пути интегрирования Ответ: Для того чтобы линейный интеграл поля не зависел от формы пути интегрирования, во-первых, необходимо и достаточно, чтобы циркуляция поля по любой замкнутой кривой равнялась нулю, во-вторых, необходимо, а для односвязного поля и достаточно, чтобы ротор поля в каждой точке равнялся нулю, в-третьих, необходимо и достаточно, чтобы подынтегральное выражение
Потенциальное поле, отыскание скалярного потенциала. Соленоидальное поле, Гармонические поля. 1)Векторное поле называется потенциальным (безвихревым полем), если в каждой его точке ротация равна нулю:
2) Скалярный потенциал векторного поля A {\displaystyle \mathbf {A} } А — это скалярная функция ϕ {\displaystyle \phi } Фи такая, что во всех точках области определения поля А=grad(фи) A = grad ϕ, {\displaystyle \mathbf {A} =\operatorname {grad} \,\phi,} Где grad(фи) grad ϕ {\displaystyle \operatorname {grad} \phi } обозначает градиент ϕ {\displaystyle \phi } Фи.
Непрерывное векторное поле в односвязной области трёхмерного пространства потенциально тогда и только тогда, когда оно безвихревое, то-есть тогда,когда Ротор равен 0. 3)Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю: 4) Гармоническим называется поле, для которого и ротор и дивергенция равны нулю.
∫ S a → ⋅ d s → = 0 {\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0} 4.8. Повторные операции теории поля. Оператор Гамильтона Ñ. Запись основных характеристик скалярного и векторного поля с помощью Ñ. Правила действия с Ñ Повторные операции теории поля
Оператор Гамильтона Ñ.
Запись основных характеристик скалярного и векторного поля с помощью Ñ.
Правила действия с Ñ
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.29.213 (0.009 с.) |

 4.4 Вычисление работы в силовом поле.
4.4 Вычисление работы в силовом поле.
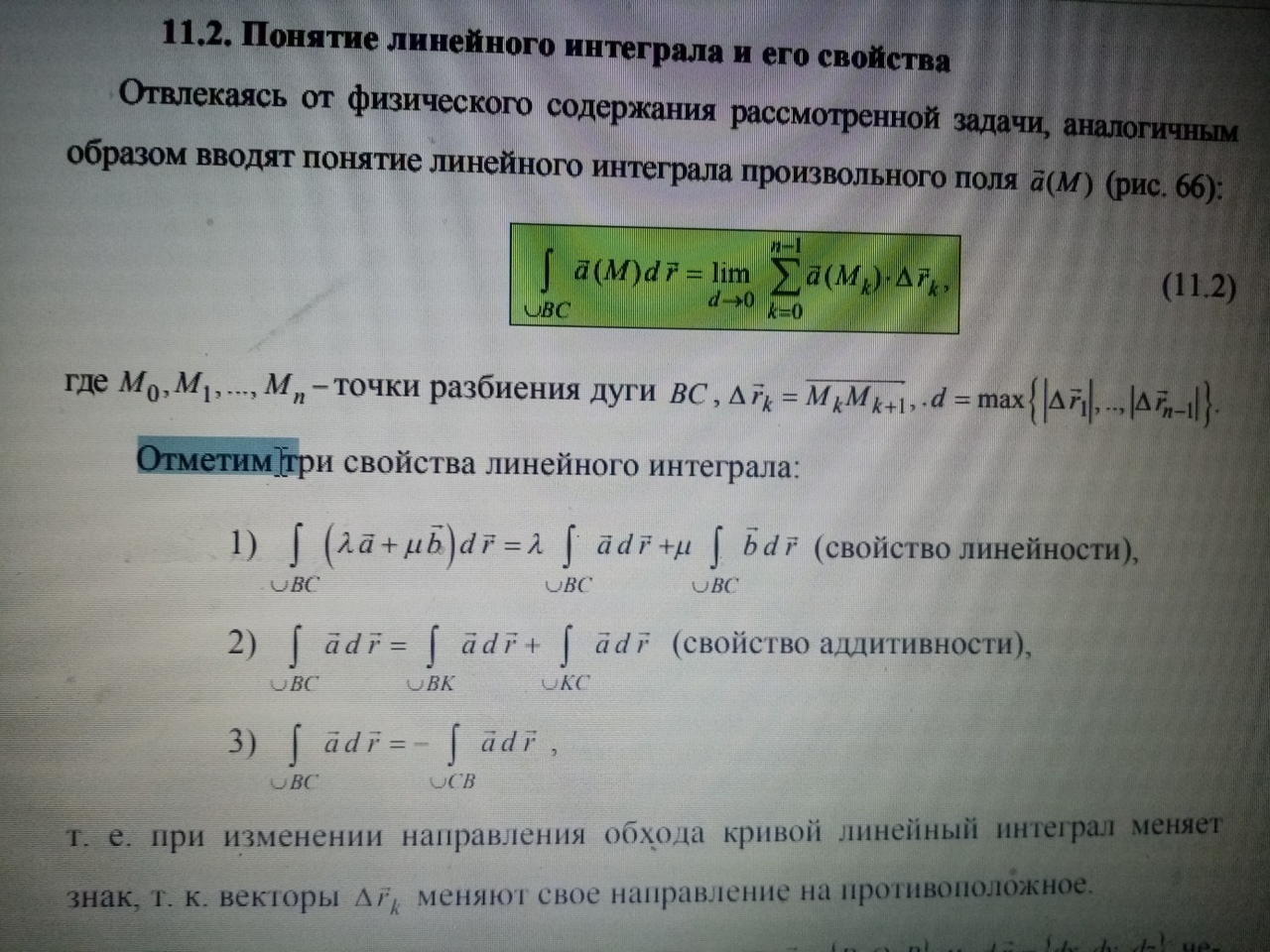
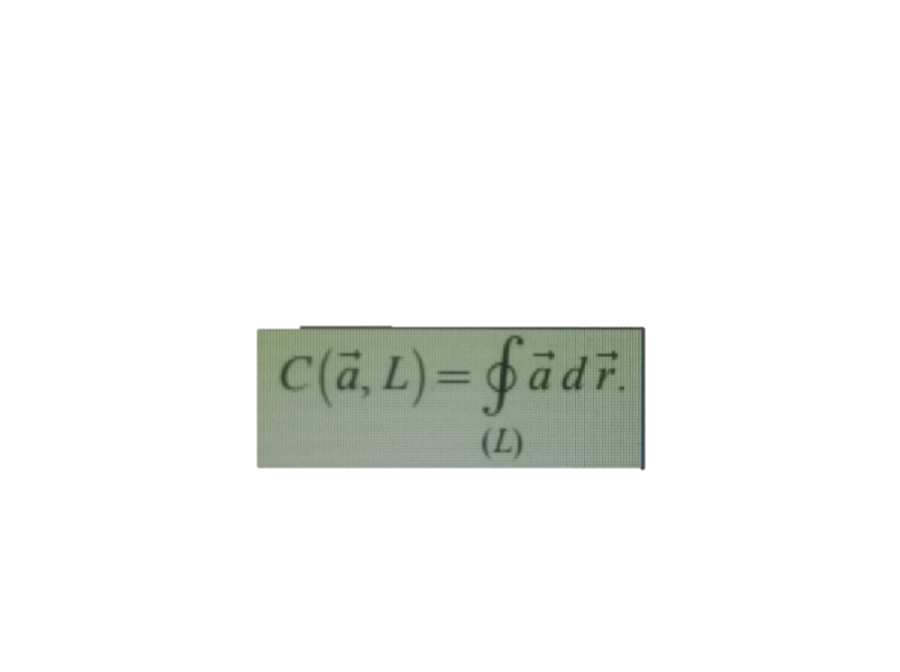 циркуляцией поля a r по кривой L и обозначается так:
циркуляцией поля a r по кривой L и обозначается так: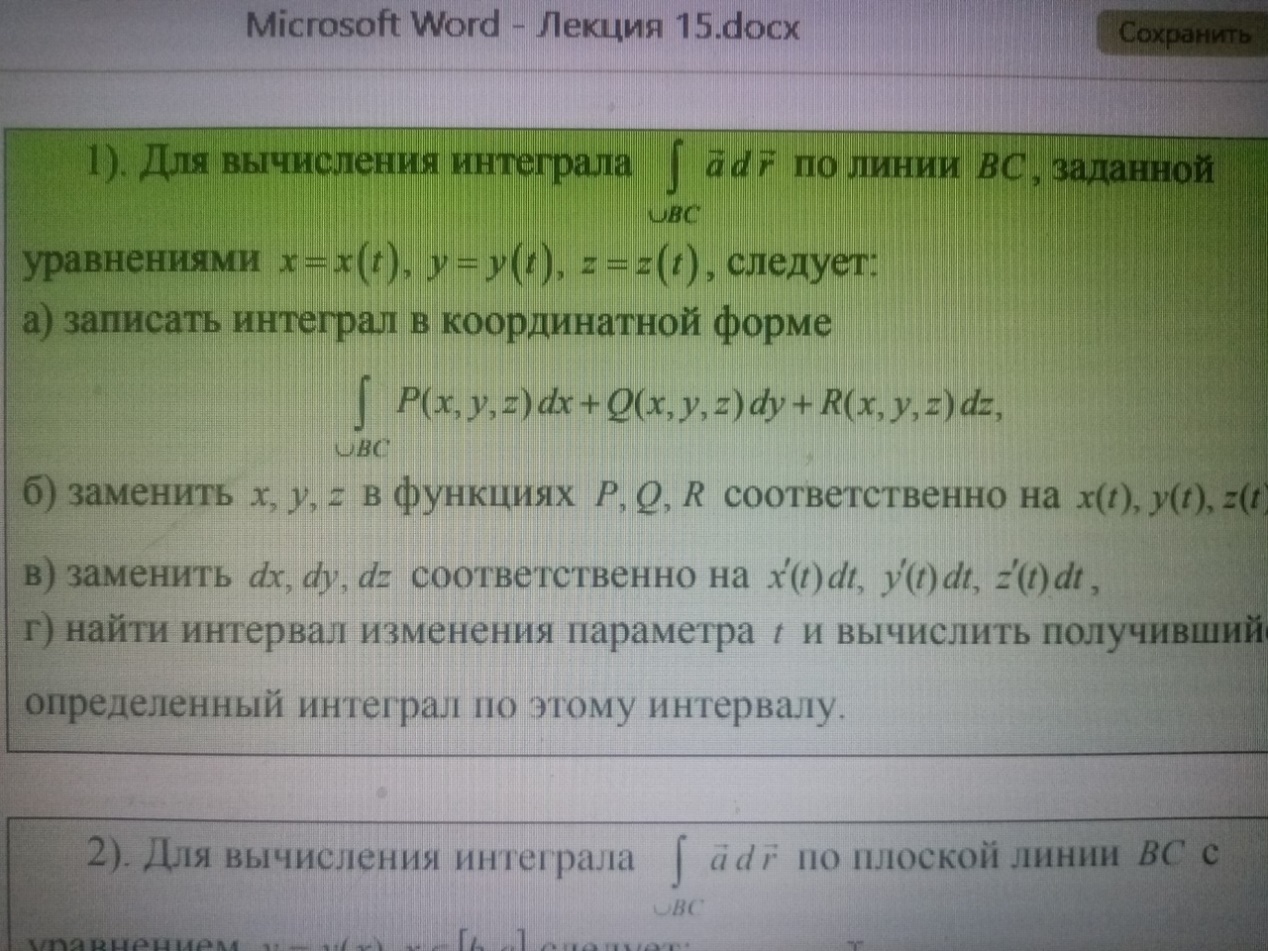

 4.5 Формула Стокса:
4.5 Формула Стокса:
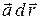 было полным дифференциалом некоторой функции
было полным дифференциалом некоторой функции 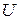 .
.