
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы Свенна и золотого сечения в определении решения на экстремум унимодальной функцииСодержание книги
Поиск на нашем сайте
Цель: закрепить теоретические знания и получить практические навыки в разработке программы решения задач методами одномерной оптимизации. Используемые приемы и технологии: технология визуального проектирования и событийного программирования, среда программирования Visual Studio 2010 Professional, язык программирования Visual C++ 2010 Professional. Ключевые термины: нелинейное моделирование, математическая модель, оптимальный план, допустимый план, алгоритм Свена, метод золотого сечения. Постановка задачи: Разработайте визуальное приложение на языке Visual C++ решения задачи методами одномерной оптимизации.
Варианты заданий
Методом Свенна найти отрезок, содержащий точку экстремума унимодальной функции Вариант 1. Вариант 2. Вариант 3. Вариант 4. Вариант 5. Вариант 6. Вариант 7. Вариант 8. Вариант 9. Вариант 10.
Методические указания
1 Разработайте алгоритм программы. 2 Разработайте визуальное приложение, формализующее алгоритм методов одномерной оптимизации: · создайте проект с помощью мастера Windows Forms Application; · настройте свойства формы Form1; · добавьте компоненты на форму; · создайте и определите функции обработчика событий. 3 Оформите отчет по лабораторной работе, включающий разделы: · Постановка задачи. · Теоретическое обоснование. · Скриншоты программы. · Код программы (функции обработчиков событий). · Выводы.
2. 3.3 Контрольные вопросы
1 Что называется нелинейным программированием? 2 Какая постановка задачи нелинейного программирования? 3 Что называется унимодальной функцией? 4 Что понимается под нелинейной моделью? 5 Какие методы одномерной оптимизации? 6 Сколько и какие этапы включает алгоритм Свенна? 7 Что понимается под золотым сечением? 8 Какое свойство золотого сечения? 9 Какие исходные данные содержит алгоритм метода золотого сечения? 10 Сколько и какие этапы метода золотого сечения?
3 Сетевое планирование и управление в моделировании информационных систем
3.1 Сетевое планирования в условиях определённости
Длина критического пути и топология определяются методом критического пути (Critical Path Method). Для определения длины критического пути рассчитывается ранний (ожидаемый) срок наступления завершающего события. Ранний срок совершения события
Поздний (предельный) срок наступления
Ранний срок начала работы – наиболее ранний (минимальный) из возможных моментов начала данной работы при заданной продолжительности работ. Совпадает с ранним сроком наступления начального события
Ранний срок окончания работы – наиболее ранний (минимальный) из возможных моментов окончания данной работы при заданной продолжительности работ. Рассчитывается по формуле
Поздний срок начала работы – наиболее поздний (максимальный) из допустимых моментов начала данной работы, при котором возможно выполнение последующих работ в установленный срок. Определяется по формуле
Поздний срок окончания работы – наиболее поздний (максимальный) из допустимых моментов окончания данной работы, при котором возможно выполнение последующих работ в установленный срок.
Работа участка, несовпадающего с критическим путем сетевого графика, обладает резервом времени. Полный резерв времени работы – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы
Критические работы не имеют резервов времени. Степень сложности выполнения в заданный срок работы некритического пути определяется коэффициентом напряженности. Коэффициент напряженности рассчитывается по формуле
Алгоритм метода критического пути. 1 Ранний и поздний сроки наступления начального события 2 Ранний и поздний сроки наступления конечного события 3 Разность между ранним сроком конечного события
3.2 Сетевое планирования в условиях неопределённости
В условиях неопределенности время Математическое ожидание рассчитывается по формуле
Дисперсия рассчитывается по формуле
Среднеквадратическое отклонение рассчитывается по формуле
Анализ сетевых графиков методом PERT (Program Evaluation and Review Technique) включает расчет временных параметров и оценку вероятности того, что общий срок выполнения проекта Если
|
||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.217 (0.007 с.) |

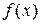 , уточнить точку экстремума методом золотого сечения,
, уточнить точку экстремума методом золотого сечения, 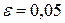 .
.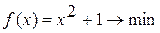
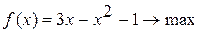
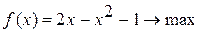
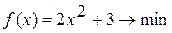
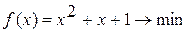
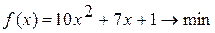
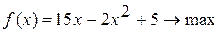
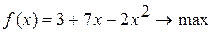
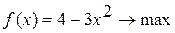
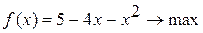
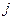 определяется по формуле
определяется по формуле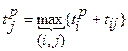 ,где (3.1)
,где (3.1)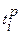 - ранний срок совершения
- ранний срок совершения 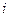 события;
события;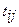 - продолжительность выполнения
- продолжительность выполнения 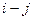 работы.
работы.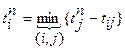 , где (3.2)
, где (3.2)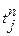 – поздний срок совершения
– поздний срок совершения 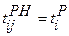 , где (3.3)
, где (3.3)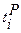 – ранний срок наступления начального события.
– ранний срок наступления начального события.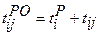 , где (3.4)
, где (3.4)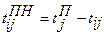 , где (3.5)
, где (3.5)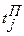 – поздний срок свершения
– поздний срок свершения 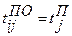 , где (3.6)
, где (3.6)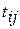 без изменения общего срока выполнения проекта. Определяется по формуле
без изменения общего срока выполнения проекта. Определяется по формуле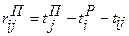 , где (3.7)
, где (3.7)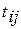 – продолжительность выполнения
– продолжительность выполнения 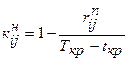 , где (3.8)
, где (3.8)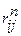 – полный резерв времени работы
– полный резерв времени работы 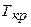 – длина критического пути;
– длина критического пути;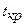 – продолжительность части максимального полного пути, содержащего работу
– продолжительность части максимального полного пути, содержащего работу 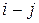 , которая совпадает с критическим путем.
, которая совпадает с критическим путем.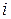 совпадают.
совпадают.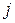 совпадают.
совпадают.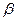 -распределение, нормальное распределение). Числовые характеристики случайной величины
-распределение, нормальное распределение). Числовые характеристики случайной величины 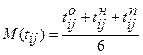 , где (3.9)
, где (3.9)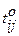 – оптимистическое время (выполнение работы в благоприятных условиях);
– оптимистическое время (выполнение работы в благоприятных условиях);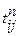 – пессимистическое время (выполнение работы в неблагоприятных условиях);
– пессимистическое время (выполнение работы в неблагоприятных условиях);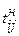 – наиболее вероятное время (выполнение работы в нормальных условиях).
– наиболее вероятное время (выполнение работы в нормальных условиях).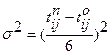 , где (3.10)
, где (3.10)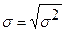 , где (3.11)
, где (3.11)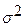 - дисперсия случайной величины
- дисперсия случайной величины 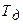 . Если вероятность
. Если вероятность 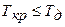 мала, например меньше 0,3, то выполнение комплекса работ в заданный срок
мала, например меньше 0,3, то выполнение комплекса работ в заданный срок 


