
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейные модели. Методы одномерной оптимизацииСодержание книги
Поиск на нашем сайте
Модели линейного программирования не всегда адекватны реальным ситуациям. При решении задач полный и точный учёт зависимостей между факторами и показателями, влияющими на критерий эффективности и ограничительные условия, достигается при разработке нелинейных математических моделей.
Постановка задачи нелинейного программирования
Задача нелинейного программирования в общем виде состоит в отыскании вектора искомых переменных
при ограничениях (2.1)
В отличие от задач линейной оптимизации, для задач нелинейного программирования общего метода, позволяющего решать любые оптимизационные задачи не существует. Это обусловлено тем, что в задачах нелинейного программирования область допустимых решений может быть невыпуклой, иметь бесконечное число крайних точек, состоять из нескольких частей, а целевая функция может достигать экстремума не только на границе, но и внутри области допустимых решений системы ограничений. Нелинейная целевая функция может иметь несколько локальных экстремумов, среди которых необходимо найти глобальный.
Методы нелинейной одномерной оптимизации
Пусть функция
Функция
Унимодальная функция монотонно возрастает слева от точки максимума и монотонно убывает справа от неё. В процессе применения методов одномерной оптимизации выделяют два этапа: · поиск отрезка, содержащего точку максимума; · уточнение координаты точки максимума на данном отрезке.
Алгоритм Свенна
Исходные данные: Этап 1. Определить Этап 2. Если Этап 3. Если Этап 4. Этап 5. Если Этап 6. Если Случай
Метод золотого сечения
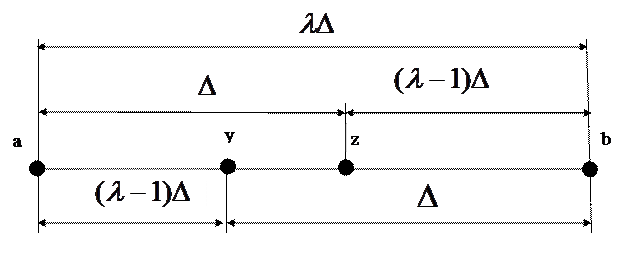
Золотое сечение отрезка – деление отрезка на две неравные части таким образом, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части отрезка. Золотое сечение отрезка
Рисунок 2.1 – Золотое сечение
Точка Алгоритм золотого сечения включает этапы: Исходные данные: Этап 1.
Этап 2. Если Этап 3.
Этап 4.
Этап 5. Если Этап 6.
Практическая работа №2
|
||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.007 с.) |

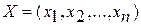 , при котором целевая функция достигает экстремума (максимума, минимума).
, при котором целевая функция достигает экстремума (максимума, минимума).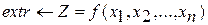
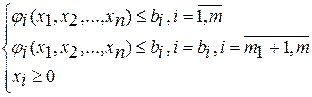
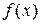 определена на
определена на 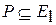 . Задача одномерной оптимизации – задача, в которой требуется найти мах(min)
. Задача одномерной оптимизации – задача, в которой требуется найти мах(min) 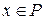 . Решение (точка максимума (минимума)) задачи одномерной оптимизации – точка
. Решение (точка максимума (минимума)) задачи одномерной оптимизации – точка 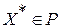 , при условии
, при условии 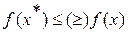 для всех
для всех 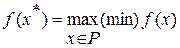 (2.2)
(2.2)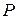 , если существует единственная точка
, если существует единственная точка 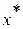 её максимума на
её максимума на 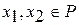 ,
,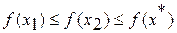 , если
, если 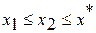 ;
;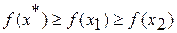 , если
, если 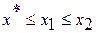
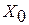 – начальная точка,
– начальная точка, 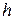 – шаг поиска (
– шаг поиска (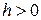 ).
).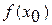 ,
,  ,
, 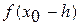 ,
, 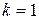 .
.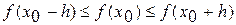 , то
, то 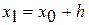 перейти на 4 этап.
перейти на 4 этап.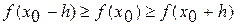 , то
, то 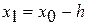 ,
, 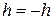 перейти на 4 этап, в противном случае (
перейти на 4 этап, в противном случае (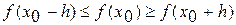 ),
), 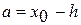 ,
, 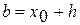 , конец.
, конец.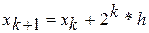 . Определить
. Определить 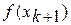 .
.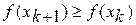 , то
, то 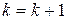 , переход на 4 этап.
, переход на 4 этап.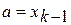 ,
, 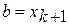 , конец. В противном случае
, конец. В противном случае 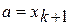 ,
, 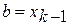 , конец.
, конец. (этап 3) не рассматривается, так как он противоречит предположению о модальности функции
(этап 3) не рассматривается, так как он противоречит предположению о модальности функции 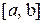 производится двумя точками
производится двумя точками 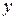 и
и 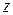 , симметричными относительно середины отрезка (рисунок 2.1).
, симметричными относительно середины отрезка (рисунок 2.1).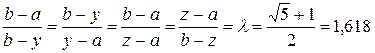
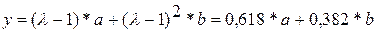
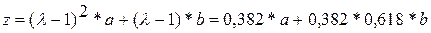
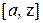 , а точка
, а точка 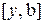 . На этом свойстве, позволяющем вычислять значение функции в одной пробной точке основан алгоритм золотого сечения.
. На этом свойстве, позволяющем вычислять значение функции в одной пробной точке основан алгоритм золотого сечения.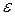 – параметр окончания счёта.
– параметр окончания счёта.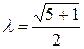 ;
; 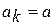 ,
, 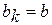 ;
;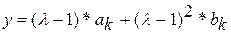 ;
; 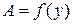 ;
;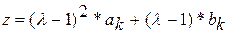 ;
; 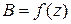 ;
;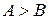 , то перейти на 4 этап.
, то перейти на 4 этап.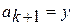 ;
; 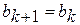 ;
;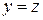 ;
; 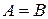 ;
;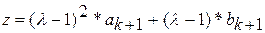 ;
;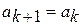 ;
;  ;
; 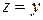 ;
; 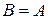 ;
;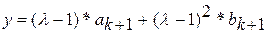 ;
;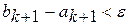 , то
, то 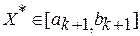 , конец.
, конец.


