
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование систем методами математического программированияСодержание книги
Поиск на нашем сайте
СЕМИНАРЫ СПЕЦИАЛИСТОВ
Методические указания к выполнению практических работ для студентов направления подготовки 09.03.04 «Программная инженерия»
Курган 2016
Кафедра: «Программное обеспечение автоматизированных систем»
Направление подготовки: 09.03.04 «Программная инженерия»
Дисциплина: «Семинары специалистов»
Составил: канд. техн. наук, доцент А.М. Семахин.
Утверждены на заседании кафедры «29» июня 2016 г.
Рекомендованы методическим советом университета
«12» декабря 2016 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 5 1 Моделирование систем методами математического программирования 5 1.1 Методы линейного программирования 5 1.1.1 Симплекс метод 6 1.1.2 Метод Гаусса-Жордана 6 1.2 Методы целочисленного программирования 7 1.2.1 Метод отсекающих плоскостей 7 2.2.2 Метод ветвей и границ 8 1.3 Практическая работа №1 «Метод отсечения в моделировании систем» 10 1.3.1 Варианты заданий 10 1.3.2 Методические указания 11 1.3.3 Контрольные вопросы 12 2 Нелинейные модели. Методы одномерной оптимизации 12 2.1 Постановка задачи нелинейного программирования 12 2.2 Методы нелинейной одномерной оптимизации 13 2.2.1 Алгоритм Свенна 13 2.2.2 Метод золотого сечения 14 2.3 Практическая работа №2. Методы Свенна и золотого сечения в определении решения на экстремум унимодальной функции 15 2.3.1 Варианты заданий 15 2.3.2 Методические указания 16 2.3.3 Контрольные вопросы 16 3 Сетевое планирование и управление в моделировании информационных систем 16 3.1 Сетевое планирования в условиях определённости 16 3.2 Сетевое планирования в условиях неопределённости 18 3.3 Расчёт параметров сетевого графика 19 3.4 Практическая работа №3. «Сетевое моделирование систем 24 3.4.1 Варианты заданий 1 24 3.4.2 Методические указания 24 3.4.3 Варианты заданий 2 25 3.4.4 Контрольные вопросы 29 4 Имитационное моделирование систем 29 4.1 Этапы имитационного моделирования 29 4.2 Структура типовой имитационной модели 29 4.3 Генерация псевдослучайных чисел 30 4.4 Моделирование случайных событий 30 4.5 Моделирование случайных величин 30 4.6 Моделирование случайных векторов 4.7 Практическая работа №4 31 «Последовательное обслуживание с блокировками и ограниченным буфером» 31 4.7.1 Варианты заданий 1 32 4.7.2 Варианты заданий 2 34 4.7.3 Методические указания 42 4.7.4 Контрольные вопросы 42 5 Системы массового обслуживания в моделировании систем 43 5.1 Основные понятия и определения. Классификация систем массового обслуживания 43 5. 2 Моделирование систем массового обслуживания 43 5.3 Модели массового обслуживания 44 5.3.1 Одноканальная система массового обслуживания с отказами в обслуживании 44 5.3.2 Многоканальная система массового обслуживания с отказами в обслуживании 45 5.3.3 Одноканальная система массового обслуживания с ограниченной длиной очереди 47 5.3.4 Одноканальная система массового обслуживания с неограниченной длиной очереди 48 5.3.5 Многоканальная система массового обслуживания с ограниченной длиной очереди 50 5.3.6 Многоканальная система массового обслуживания с неограниченной длиной очереди 51 5.4 Практическая работа №5. Модели систем массового обслуживания 53 5.4.1 Варианты заданий 54 5.4.2 Методические указания 55 5.4.3 Контрольные вопросы 56 ЗАКЛЮЧЕНИЕ 56 СПИСОК ЛИТЕРАТУРЫ 56
ВВЕДЕНИЕ
Дисциплина «Семинары специалистов» (6 семестр) имеет целью дать студентам теоретические знания и практические навыки в разработке математических моделей и формализации алгоритмов методов решения на объектно-ориентированном языке программирования. Предмет дисциплины – технология разработки математических моделей. Задачи дисциплины – изучение теоретических основ математического моделирования процессов, явлений и объектов реального мира и приобретение практических навыков разработки программных приложений в интегрированной среде программирования Microsoft Visual Studio, отладки и документирования программ. Практические занятия (34 часов). Методические указания содержат теоретическое обоснование и варианты заданий для выполнения практических работ по дисциплине «Семинары специалистов». Методические указания разработаны в соответствии с требованиями государственного образовательного стандарта по подготовке бакалавров по направлению 09.03.04 – «Программная инженерия».
Симплекс метод
Симплекс-метод – метод обхода угловых точек области допустимых решений (симплекса) с проверкой на оптимальность. Базисное решение – решение системы уравнений, получаемое приравниванием к нулю Допустимое базисное решение – базисное решение, удовлетворяющее требованию неотрицательности правых частей. Небазисные переменные – переменные, имеющие нулевое значение. Базисные переменные – переменные, имеющие ненулевое значение. Включаемая переменная – небазисная переменная, которая будет включена в множество базисных переменных на следующей итерации (при переходе к смежной экстремальной точке). Исключаемая переменная – базисная переменная, которая на следующей итерации подлежит исключению из множества базисных переменных. Симплекс-алгоритм состоит из следующих шагов. Шаг 1. Определение начального допустимого базисного решения. Шаг 2. Определение включаемой переменной из числа небазисных переменных. Если такой переменной нет, то решение оптимально. Иначе осуществляется переход к шагу 3. Шаг 3. Определение исключаемой переменной из числа базисных переменных. Шаг 4. Определение нового базисного решения. Переход на шаг 2 [2].
Метод Гаусса-Жордана
Метод Гаусса-Жордана (метод исключения переменных) определяет оптимальное решение задачи линейного программирования. Метод Гаусса-Жордана выполняется после определения ведущей строки, ведущего столбца и ведущего элемента симплекс-таблицы. Ведущая строка – строка симплекс-таблицы, соответствующая исключаемой переменной. Ведущий столбец – столбец симплекс-таблицы, соответствующий включаемой переменной. Ведущий элемент – элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки. Условие оптимальности. Включаемой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая в Z-уравнении наибольший отрицательный (положительный) коэффициент. В случае равенства коэффициентов для нескольких небазисных переменных выбор делается произвольно. Если все коэффициенты при небазисных переменных в Z-уранении неотрицательны (неположительны), полученное решение является оптимальным [2]. Условие допустимости. В задачах максимизации и минимизации в качестве исключаемой переменной выбирается базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к (положительному) коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно [2]. Метод Гаусса-Жордана включает две вычислительные процедуры. 1 Формирование новой ведущей строки. Новая ведущая строка=Старая ведущая строка/Ведущий элемент. 2 Формирование остальных новых уравнений. Новое уравнение=Старое уравнение–(Коэффициент ведущего столбца старого уравнения)*(Новая ведущая строка) [2]
Метод отсекающих плоскостей
Метод отсекающих плоскостей разработан Р. Гомори в 1957-1958 годах. Алгоритм метода включает этапы: Этап 1. Ослабленная задача. Целочисленность искомых переменных игнорируется, симплекс-методом определяется оптимальный план. Этап 2. Расширенная задача. Если план нецелочисленный, составляется дополнительное ограничение, “отсекающее” дробную часть искомой переменной. Дополнительное ограничение включается в систему ограничений и решается расширенная задача [3].
Метод ветвей и границ
Метод ветвей и границ применяется для решения полностью или частично целочисленных задач. Предложен А Лэндом и Дж. Дойгом в 1960 г. Дана математическая модель целочисленного линейного программирования
при ограничениях (1.3)
Найти вектор
В начале 1. Список задач линейного программирования, каждая из которых должна быть решена в последующих итерациях. 2. Нижнюю границу оптимального значения линейной формы задачи Пусть в результате 1 Этап. Выбирается из списка задач линейного программирования задача 2 Этап. Если задача 3 Этап. Если 4 Этап. Если все компоненты вектора 5 Этап Задача
при ограничениях
Тогда задача
при ограничениях
Процесс решения продолжается пока не будут решены все задачи линейного программирования из списка. Решение задачи будет
Практическая работа №1 «Метод отсечения в моделировании систем»
Цель: получить теоретические знания и практические навыки в моделировании систем методами линейного программирования. Используемые приемы и технологии: линейное программирование, целочисленное программирование. Ключевые термины: математическая модель, симплекс-метод, метод отсекающих плоскостей, метод ветвей и границ. Постановка задачи: Разработайте математическую модель выбора оптимального проекта информационной системы организации. Разработайте программу, формализующую математическую модель выбора оптимального проекта информационной системы организации на языке С++.
Варианты заданий
Разработайте программу на языке С++, формализующую алгоритм решения оптимизационной задачи симплекс-методом
Вариант 1 Вариант 2 Вариант 3
при ограничениях при ограничениях при ограничениях
Вариант 4 Вариант 5 Вариант 6
при ограничениях при ограничениях при ограничениях
Вариант 7 Вариант 8 Вариант 9
при ограничениях при ограничениях при ограничениях
Вариант 10 Вариант 11 Вариант 12
при ограничениях при ограничениях при ограничениях
Методические указания
1 Выбрать вариант задания по последней цифре номера зачетной книжки. 2 Разработать математическую модель выбора оптимального проекта информационной системы. 3 Разработать алгоритм решения задачи. 4 Разработать программу выбора оптимального проекта информационной системы. 5 Оформить отчет по практической работе. Содержание отчета должно включать: Титульный лист 1 Постановка задачи. 2 Описание алгоритма решения задачи 3 Математическая модель выбора проекта информационной системы организации. 4 Диаграмма классов. 5 Оптимальное решение математической модели информационной системы.
1.3. 3 Контрольные вопросы
1 Что называется математической моделью? 2 Что называется оптимальным решением? 3 Что называется допустимым решением? 4 Какие этапы метода Гаусса-Жордана? 5 Какой алгоритм метода обыкновенное Жорданово исключение? 6 Какой алгоритм метода модифицированное Жорданово исключение? 7 Какие этапы алгоритма метода отсекающих плоскостей? 8 Какие этапы алгоритма метода ветвей и границ? 9 Как формулируется условие оптимальности? 10 Как формулируется условие допустимости?
Алгоритм Свенна
Исходные данные: Этап 1. Определить Этап 2. Если Этап 3. Если Этап 4. Этап 5. Если Этап 6. Если Случай
Метод золотого сечения
Золотое сечение отрезка – деление отрезка на две неравные части таким образом, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части отрезка. Золотое сечение отрезка
Рисунок 2.1 – Золотое сечение
Точка Алгоритм золотого сечения включает этапы: Исходные данные: Этап 1.
Этап 2. Если Этап 3.
Этап 4.
Этап 5. Если Этап 6.
Практическая работа №2 Варианты заданий
Методом Свенна найти отрезок, содержащий точку экстремума унимодальной функции Вариант 1. Вариант 2. Вариант 3. Вариант 4. Вариант 5. Вариант 6. Вариант 7. Вариант 8. Вариант 9. Вариант 10.
Методические указания
1 Разработайте алгоритм программы. 2 Разработайте визуальное приложение, формализующее алгоритм методов одномерной оптимизации: · создайте проект с помощью мастера Windows Forms Application; · настройте свойства формы Form1; · добавьте компоненты на форму; · создайте и определите функции обработчика событий. 3 Оформите отчет по лабораторной работе, включающий разделы: · Постановка задачи. · Теоретическое обоснование. · Скриншоты программы. · Код программы (функции обработчиков событий). · Выводы.
2. 3.3 Контрольные вопросы
1 Что называется нелинейным программированием? 2 Какая постановка задачи нелинейного программирования? 3 Что называется унимодальной функцией? 4 Что понимается под нелинейной моделью? 5 Какие методы одномерной оптимизации? 6 Сколько и какие этапы включает алгоритм Свенна? 7 Что понимается под золотым сечением? 8 Какое свойство золотого сечения? 9 Какие исходные данные содержит алгоритм метода золотого сечения? 10 Сколько и какие этапы метода золотого сечения?
3 Сетевое планирование и управление в моделировании информационных систем
3.1 Сетевое планирования в условиях определённости
Длина критического пути и топология определяются методом критического пути (Critical Path Method). Для определения длины критического пути рассчитывается ранний (ожидаемый) срок наступления завершающего события. Ранний срок совершения события
Поздний (предельный) срок наступления
Ранний срок начала работы – наиболее ранний (минимальный) из возможных моментов начала данной работы при заданной продолжительности работ. Совпадает с ранним сроком наступления начального события
Ранний срок окончания работы – наиболее ранний (минимальный) из возможных моментов окончания данной работы при заданной продолжительности работ. Рассчитывается по формуле
Поздний срок начала работы – наиболее поздний (максимальный) из допустимых моментов начала данной работы, при котором возможно выполнение последующих работ в установленный срок. Определяется по формуле
Поздний срок окончания работы – наиболее поздний (максимальный) из допустимых моментов окончания данной работы, при котором возможно выполнение последующих работ в установленный срок.
Работа участка, несовпадающего с критическим путем сетевого графика, обладает резервом времени. Полный резерв времени работы – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы
Критические работы не имеют резервов времени. Степень сложности выполнения в заданный срок работы некритического пути определяется коэффициентом напряженности. Коэффициент напряженности рассчитывается по формуле
Алгоритм метода критического пути. 1 Ранний и поздний сроки наступления начального события 2 Ранний и поздний сроки наступления конечного события 3 Разность между ранним сроком конечного события
3.2 Сетевое планирования в условиях неопределённости
В условиях неопределенности время Математическое ожидание рассчитывается по формуле
Дисперсия рассчитывается по формуле
Среднеквадратическое отклонение рассчитывается по формуле
Анализ сетевых графиков методом PERT (Program Evaluation and Review Technique) включает расчет временных параметров и оценку вероятности того, что общий срок выполнения проекта Если
Практическая работа №3 «Сетевое моделирование систем»
Цель: получить теоретические знания и практические навыки в моделировании процессов управления комплексом работ. Используемые приемы и технологии: сетевое планирование и управление, сетевое моделирование в условиях определённ
|
||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.108 (0.009 с.) |

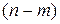 переменных, где
переменных, где 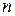 – количество неизвестных,
– количество неизвестных, 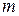 – количество уравнений.
– количество уравнений.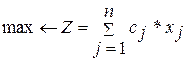
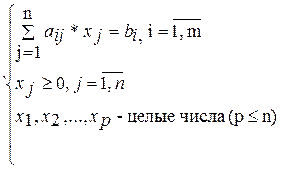
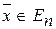 , максимизирующий целевую функцию. Для целочисленной переменной можно указать верхнюю и нижнюю границы, в пределах которых содержатся оптимальные значения
, максимизирующий целевую функцию. Для целочисленной переменной можно указать верхнюю и нижнюю границы, в пределах которых содержатся оптимальные значения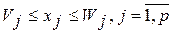 . (1.4)
. (1.4)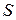 итерации метода ветвей и границ необходимо иметь:
итерации метода ветвей и границ необходимо иметь: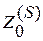 . На первой итерации в качестве
. На первой итерации в качестве 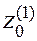 берется значение целевой функции
берется значение целевой функции 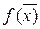 в любой целочисленной точке
в любой целочисленной точке 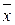 . Если точку указать невозможно, то принимают
. Если точку указать невозможно, то принимают 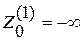 .
.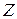 задач:
задач: 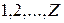 и существует
и существует 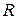 для решения,
для решения, 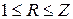 . Задача
. Задача 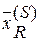 , то переходим к этапу 3. Иначе – исключаем задачу
, то переходим к этапу 3. Иначе – исключаем задачу 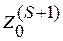 =
= 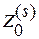 . Переход к этапу 1. При
. Переход к этапу 1. При 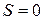 делаем вывод, что исходная задача не имеет решения и процесс решения заканчивается.
делаем вывод, что исходная задача не имеет решения и процесс решения заканчивается.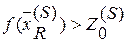 , то переходим к этапу 4. В противном случае задача
, то переходим к этапу 4. В противном случае задача 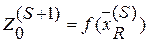 . Переход к этапу 1. При
. Переход к этапу 1. При 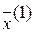 является решением исходной задачи и процесс решения заканчивается.
является решением исходной задачи и процесс решения заканчивается.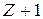 и задача
и задача 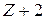 ,
, 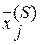 - дробная компонента в полученном оптимальном плане
- дробная компонента в полученном оптимальном плане 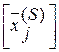 целая часть. Тогда задача
целая часть. Тогда задача 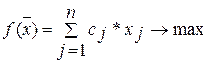
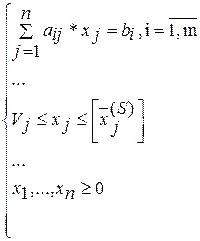 (1.5)
(1.5)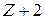 имеет вид:
имеет вид: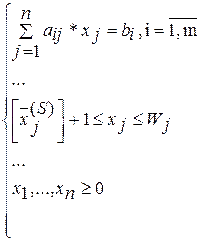 (1.6)
(1.6)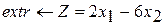
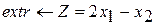
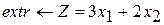
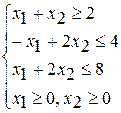
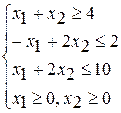
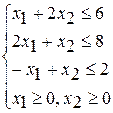
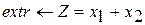
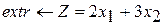
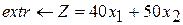
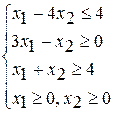
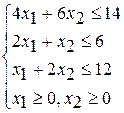
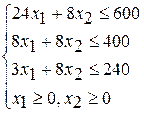
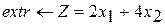
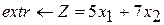
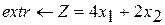
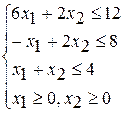
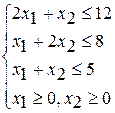
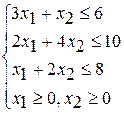
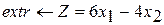
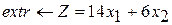

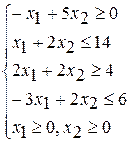
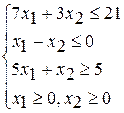
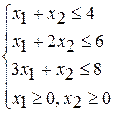
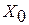 – начальная точка,
– начальная точка, 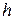 – шаг поиска (
– шаг поиска (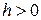 ).
).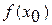 ,
,  ,
, 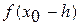 ,
, 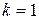 .
.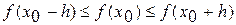 , то
, то 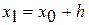 перейти на 4 этап.
перейти на 4 этап.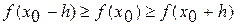 , то
, то 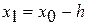 ,
, 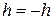 перейти на 4 этап, в противном случае (
перейти на 4 этап, в противном случае (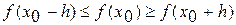 ),
), 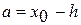 ,
, 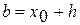 , конец.
, конец.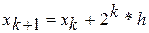 . Определить
. Определить 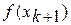 .
.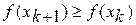 , то
, то 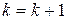 , переход на 4 этап.
, переход на 4 этап.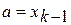 ,
, 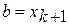 , конец. В противном случае
, конец. В противном случае 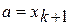 ,
, 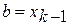 , конец.
, конец. (этап 3) не рассматривается, так как он противоречит предположению о модальности функции
(этап 3) не рассматривается, так как он противоречит предположению о модальности функции 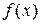 .
.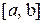 производится двумя точками
производится двумя точками 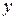 и
и 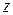 , симметричными относительно середины отрезка (рисунок 2.1).
, симметричными относительно середины отрезка (рисунок 2.1).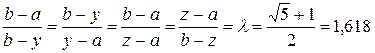
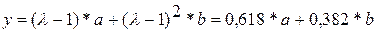
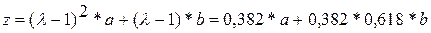
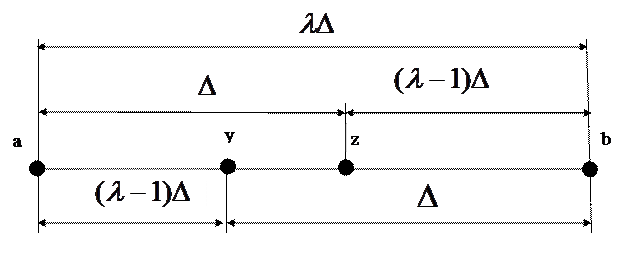
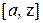 , а точка
, а точка 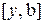 . На этом свойстве, позволяющем вычислять значение функции в одной пробной точке основан алгоритм золотого сечения.
. На этом свойстве, позволяющем вычислять значение функции в одной пробной точке основан алгоритм золотого сечения.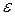 – параметр окончания счёта.
– параметр окончания счёта.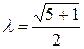 ;
; 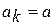 ,
, 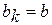 ;
;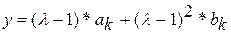 ;
; 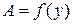 ;
;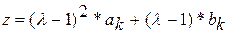 ;
; 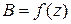 ;
;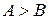 , то перейти на 4 этап.
, то перейти на 4 этап.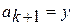 ;
; 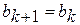 ;
;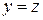 ;
; 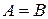 ;
;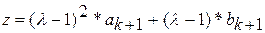 ;
;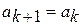 ;
;  ;
; 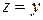 ;
; 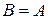 ;
;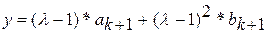 ;
;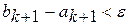 , то
, то 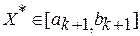 , конец.
, конец.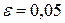 .
.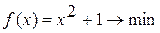
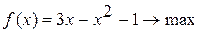
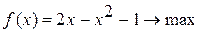
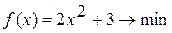
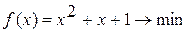
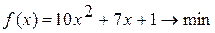
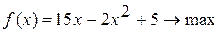
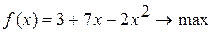
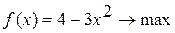
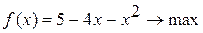
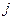 определяется по формуле
определяется по формуле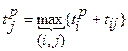 ,где (3.1)
,где (3.1)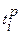 - ранний срок совершения
- ранний срок совершения 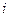 события;
события;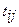 - продолжительность выполнения
- продолжительность выполнения 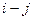 работы.
работы.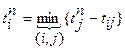 , где (3.2)
, где (3.2)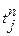 – поздний срок совершения
– поздний срок совершения 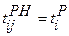 , где (3.3)
, где (3.3)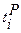 – ранний срок наступления начального события.
– ранний срок наступления начального события.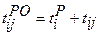 , где (3.4)
, где (3.4)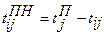 , где (3.5)
, где (3.5)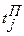 – поздний срок свершения
– поздний срок свершения 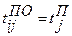 , где (3.6)
, где (3.6)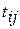 без изменения общего срока выполнения проекта. Определяется по формуле
без изменения общего срока выполнения проекта. Определяется по формуле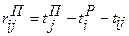 , где (3.7)
, где (3.7)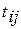 – продолжительность выполнения
– продолжительность выполнения 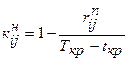 , где (3.8)
, где (3.8)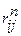 – полный резерв времени работы
– полный резерв времени работы 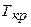 – длина критического пути;
– длина критического пути;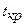 – продолжительность части максимального полного пути, содержащего работу
– продолжительность части максимального полного пути, содержащего работу 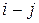 , которая совпадает с критическим путем.
, которая совпадает с критическим путем.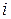 совпадают.
совпадают.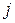 совпадают.
совпадают.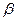 -распределение, нормальное распределение). Числовые характеристики случайной величины
-распределение, нормальное распределение). Числовые характеристики случайной величины 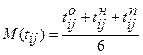 , где (3.9)
, где (3.9)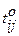 – оптимистическое время (выполнение работы в благоприятных условиях);
– оптимистическое время (выполнение работы в благоприятных условиях);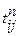 – пессимистическое время (выполнение работы в неблагоприятных условиях);
– пессимистическое время (выполнение работы в неблагоприятных условиях);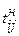 – наиболее вероятное время (выполнение работы в нормальных условиях).
– наиболее вероятное время (выполнение работы в нормальных условиях).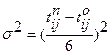 , где (3.10)
, где (3.10)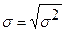 , где (3.11)
, где (3.11)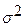 - дисперсия случайной величины
- дисперсия случайной величины 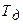 . Если вероятность
. Если вероятность 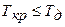 мала, например меньше 0,3, то выполнение комплекса работ в заданный срок
мала, например меньше 0,3, то выполнение комплекса работ в заданный срок 


