
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение к конъюнктивной нормальной форме.Содержание книги Поиск на нашем сайте
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Пример КНФ: ( Пусть ДНФ F имеет вид F = Процедура приведения ДНФ к КНФ: 1. Применить к F правило двойного отрицания F = F = 2. С помощью правил де Моргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции F = 5. Двойственность. Функция f *( Отношение двойственности между функциями симметрично, т.е. если f * двойственна к f, то f двойственна к f *:
Функция, двойственная к самой себе, называется самодвойственной. Принцип двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F * будет представлять функцию f *, двойственную f. Принцип двойственности в булевой алгебре: если в формуле F, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F *, представляющую функцию f *, двойственную f. Пример 1. Доказать справедливость обобщенного склеивания методом эквивалентных преобразований. Выполним эквивалентные преобразования:
Пример 2. Получить СДНФ функции, используя эквивалентные соотношения: f (x, y, z, u)= xy Ú xz Ú zu.
f(x, y, z, u)
Пример 3. Упростить булевы формулы: а) б) f (x, y, z)
а)
б) f (x, y, z) 0×
Пример 4. Представить булеву формулу
б)
Пример 5. Упростить СДНФ функции f (x, y, z, u)
Для эффективного упрощения СДНФ используем метод Блейка-Порецкого. Метод заключается в попарном склеивании всех элементарных конъюнкций СДНФ между собой, а также полученных в процессе склеивания элементарных конъюнкций меньшего числа переменных и затем – поглощении конъюнкциями меньшего числа переменных конъюнкций большего числа переменных. Рассмотрим метод Блейка-Порецкого “в действии”, для чего пронумеруем элементарные конъюнкции СДНФ:
1 2 3 4 5 6 7 Выполним все возможные попарные склеивания элементарных конъюнкций в СДНФ (под результатом склеивания проставим номера склеиваемых конъюнкций):
1,6 1,7 2,3 2,4 2,5 3,7 4,6 4,7 5,6 Выполним все возможные попарные склеивания полученных элементарных конъюнкций трех переменных:
1,6 1,7 2,3 2,4 2,4 2,5 4,7 4,6 4,7 3,7 5,6 4,6 Очевидно, что дальнейшее склеивание в данном примере невозможно. Объединим символом Ú все полученные дизъюнкции элементарных конъюнкций. Таким образом, в результате попарного склеивания получили: f (x, y, z, u)
Выполним теперь в этом выражении поглощение, в результате чего получим: f (x, y, z, u)=
Пример 6. Привести к ДНФ формулу:
Пример 7. Привести формулу к КНФ: f (x, y, z)
Пример 8. Получить СКНФ функции f (x, y, z, u) из примера 2.
В примере 2 для заданной функции f (x, y, z, u)= xy Ú xz Ú zu была получена СДНФ: f (x, y, z, u) Воспользуемся этими данными для получения СКНФ, для чего определим единичное множество функции f (x, y, z, u), т.е. множество наборов, на которых f =1:{(1111),(1101),(1110),(1100),(1011),(1010), (0111),(0011)}. Всего наборов функции четырех переменных 24=16. Определим теперь нулевое множество для f (x, y, z, u), т.е. множество наборов, на которых f =0: {(0000),(0001),(0010),(0100),(0101),(0110),(1000), (1001)}. Отсюда по правилу построения СКНФ из нулевого множества функции: f (x, y, z, u)
Пример 9. Доказать справедливость принципа двойственности в булевой алгебре, исходя из общего принципа двойственности.
Найдем для каждой операции булевой алгебры (
Таким образом, конъюнкция двойственна дизъюнкции, дизъюнкция – конъюнкции, а отрицание самодвойственно. Наконец, константы 0 и 1 принадлежат множеству логических функций Отсюда следует справедливость принципа двойственности в булевой алгебре.
Пример 10. Пусть f (x, y, z) а) определения двойственности функции; б) принципа двойственности в булевой алгебре.
б) f *(x, y, z)
Вопросы для самопроверки и упражнения. 1. Доказать методом эквивалентных преобразований справедливость соотношений п.11, п.12, п.13. 2. Упростить СДНФ импликации и функции Шеффера, используя эквивалентные соотношения. 3. Логическая функция а) табличное представление функции f; б) расщепление (обратное склеивание). 4. Для функций, заданных в виде ДНФ, получить СДНФ, используя эквивалентные преобразования, и упростить СДНФ, использую метод Блейка-Порецкого, описанный в примере 5. а) f (x, y, z) б) f (x, y, z) в) f (x, y, z)
6. Для функций 1) получить КНФ, используя правило приведения ДНФ к КНФ; 2) найти СДНФ и СКНФ, используя табличное представление функции. 7. Подтвердить самодвойственность функции f (x, y, z)= 8. Для функции 1) определения двойственной функции; 2) принципа двойственности в булевой алгебре: а) б) в) 9. Методом эквивалентных преобразований подтвердить справедливость правил 9, 12 §1.2 логически правильных рассуждений. 10. Убедиться в неправильности рассуждений а)–в), приведенных в §1.2: а) стандартным методом; б) методом эквивалентных преобразований.
|
|||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.153 (0.007 с.) |

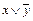 )(
)(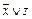 )(
)(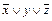 ).
).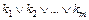 , где
, где 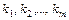 – элементарные конъюнкции.
– элементарные конъюнкции.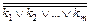 и привести
и привести 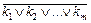 к ДНФ
к ДНФ 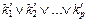 , где
, где 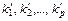 – элементарные конъюнкции. Тогда
– элементарные конъюнкции. Тогда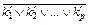 .
.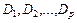 . Тогда
. Тогда ×
× 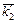 ×...×
×...× 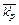 =
= 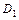 ×
× 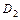 ×...×
×...× 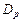
 ,...,
,...,  ) называется двойственной к функции f (
) называется двойственной к функции f (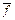 (
(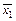 ,...,
,..., 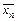 ).
).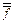 (
(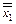 ,...,
,..., 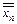 )= f *(
)= f *( ,...,
,..., 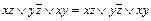 ×1
×1 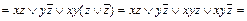
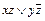 .
.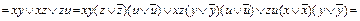
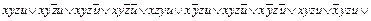
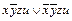 =
= 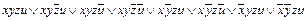 .
.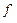 (
( ,
,  )
) 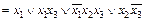 ;
;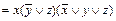 .
.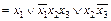
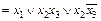
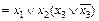
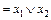 ×1
×1 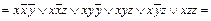
 Ú 0× z Ú x ×0Ú xyz Ú
Ú 0× z Ú x ×0Ú xyz Ú 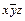 Ú xzz
Ú xzz 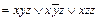
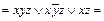
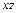 .
.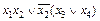 в базисе {&,Ø} и {Ú,Ø}.
в базисе {&,Ø} и {Ú,Ø}.


 а)
а) 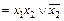
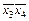
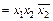
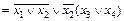
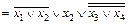 .
.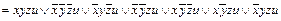
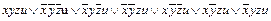
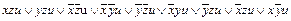
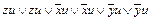
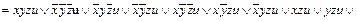
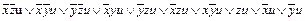 .
.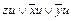
 f (x, y, z)=
f (x, y, z)= 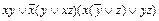 .
.

 f (x, y, z)
f (x, y, z) 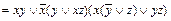
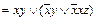
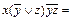
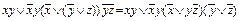
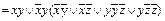
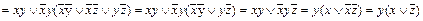
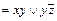 .
.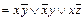 .
.







 f (x, y, z)
f (x, y, z) 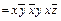
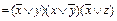
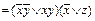
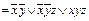
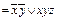
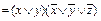 .
. .
.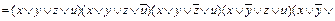
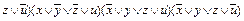 .
.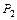 ; &, Ú, Ø) двойственные им операции.
; &, Ú, Ø) двойственные им операции. а) Пусть f (x, y)= x × y. Тогда f *(x, y)
а) Пусть f (x, y)= x × y. Тогда f *(x, y) 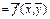

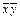
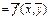
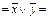 x × y.
x × y. в) Пусть f (x)
в) Пусть f (x) 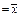 . Тогда f *(x)
. Тогда f *(x) 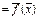
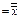
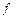 (
(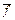 (
(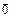
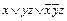 . Найти ДНФ двойственной функции f *(x, y, z), исходя из:
. Найти ДНФ двойственной функции f *(x, y, z), исходя из:


 а) f *(x, y, z)
а) f *(x, y, z) 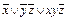
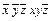
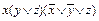
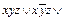
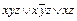
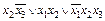 . Упростить формулу и получить СДНФ, используя:
. Упростить формулу и получить СДНФ, используя: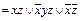 ; г) f (x, y, z)
; г) f (x, y, z) 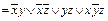 ;
;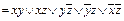 ; д) f (x, y, z)
; д) f (x, y, z) 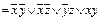 .
. ;
; 5. Привести формулы к ДНФ:
5. Привести формулы к ДНФ:
 а)
а) 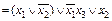 ;
; б)
б) 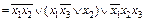 ;
;


 в)
в) 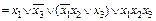 ;
;

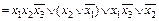 .
.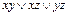 , используя принцип двойственности в булевой алгебре.
, используя принцип двойственности в булевой алгебре.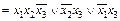 ;
;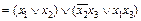 ;
;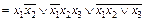 .
.


