
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Префиксная нормальная форма.Содержание книги Поиск на нашем сайте
Формулы называются эквивалентными, если при любых подстановках констант они принимают одинаковые значения. В частности, все ТИ-формулы (и все ТЛ-формулы) эквивалентны. Если формулы Множество ТИ-формул логики предикатов входит в любую теорию, исследование этого множества – важная цель логики предикатов. При этом выделяются две проблемы: 1) получение ТИ-формул (проблема построения порождаящей процедуры для множества ТИ-формул); 2) проверка формулы на истинность (проблема разрешающей процедуры). В логике предикатов прямой перебор всех переменных может быть невозможен, если предметные переменные имеют бесконечные области определения. Поэтому в логики предикатов используются различные косвенные приемы, в том числе эквивалентные соотношения, позволяющие выполнить корректные преобразования предикатных формул. В логике (алгебре) предикатов справедливы все эквивалентные соотношения логики (алгебры) высказываний, а также собственные эквивалентные соотношения, включающие связки " и $ (ниже под Y будем понимать переменное высказывание или формулу, не содержащую x): Ø$ x P (x)~" x Ø P (x). (4.1) Ø" x P (x)~$ x Ø P (x). (4.2) " x ( $ x ( " x " y P (x, y)~" y " x P (x, y). (4.5) $ x $ y P (x, y)~$ y $ x P (x, y). (4.6) " x (P (x)& Y)~(" x P (x)& Y). (4.7) " x (P (x)Ú Y)~(" x P (x)Ú Y). (4.8) $ x (P (x)& Y)~($ x P (x)& Y). (4.9) $ x (P (x)Ú Y)~($ x P (x)Ú Y). (4.10) Указанных соотношений, а также эквивалентных соотношений логики (алгебры) высказываний достаточно для выполнения преобразований формул логики (алгебры) предикатов.
Как и в логике высказываний, в логике предикатов существуют эквивалентные нормальные формы представления любых предикатных формул, в том числе префиксная (или пренексная) нормальная форма. Префиксной нормальной формой (ПНФ) называется формула, имеющая вид: Процедура получения ПНФ: 2. Используя формулы
заменить операции ®,~ на &,Ú,Ø. 2. Воспользовавшись выражениями (4.1), (4.2), а также правилом двойного отрицания и правилами де Моргана ØØ P = P, (4.13) Ø( Ø( представить предикатную формулу таким образом, чтобы символы отрицания были расположены непосредственно перед символами предикатов. 3. Для формул, содержащих подформулы вида " x ввести новые переменные, позволяющие использовать соотношения (4.7) – (4.10). 4. С помощью формул (4.3) – (4.10) получить формулы в виде ПНФ. Пример 1. В соответствии с соотношениями (4.3) – (4.4) квантор общности обладает свойством дистрибутивности относительно конъюнкции, а квантор существования – относительно дизъюнкции. Показать, что если в указанных формулах поменять местами кванторы " x и $ x, то полученные при этом соотношения будут верны лишь в одну сторону: $ x ( (" x
В соотношениях (4.16) и (4.17) левая часть более сильная, чем правая, поскольку она требует для своей истинности выполнения более жестких условий, чем правая. Так, в левой части (4.16) требуется, чтобы
Из доказанного следует, что в рассмотренных случаях нельзя непосредственно получить ПНФ предикатной формулы. Ее удается построить введением новых переменных: $ x " x
Пример 2. Привести к ПНФ следующую предикатную формулу: Ø($ x " y
Поскольку в данной предикатной формуле имеются два высказывания $ x " y Ø($ x " y Воспользуемся далее эквивалентным соотношением (4.1): Ø$ x " y Продолжая перемещение символов отрицания непосредственно к символам предикатов, используем соотношение (4.2): " x Ø" y Так как квантор общности " x не дистрибутивен относительно дизъюнкции Ú, поменяем в каком-либо предикате, например, во втором, переменную x на новую переменную z: " x $ y Ø Воспользовавшись дважды эквивалентным соотношением (4.8) или соотношением (4.19), получим: " x $ y Ø Поскольку квантор существования $ y дистрибутивен относительно дизъюнкции Ú (см. 4.4), окончательно получим префиксную нормальную форму для исходной предикатной формулы: " x " z ($ y Ø
Пример 3. Получить ПНФ предикатной формулы: " x " y ($ z (
Для получения ПНФ удалим из исходной формулы связку ®, используя формулу булевой алгебры (4.12): " x " y ($ z ( Избавимся от отрицания перед квантором $ z, используя (4.1): " x " y (Ø$ z ( Воспользуемся далее правилом де Моргана (4.15): " x " y (" z Ø( Так как последний предикат не зависит от переменной z, используем соотношение (4.8): " x " y (" z (Ø Аналогично для вынесения квантора " u (благодаря независимости первых предикатов от переменной u) воспользуемся (4.10): " x " y " z (Ø Полученная в результате выполненных эквивалентных преобразований формула является ПНФ исходной формулы.
Пример 4. Получить ПНФ предикатной формулы (Ø$ u
Для получения ПНФ осуществим эквивалентные преобразования, указывая каждый раз справа номер используемого эквивалентного соотношения:
(Ø$ u (ØØ$ u ($ u Ø($ u (Ø$ u (Ø$ u (" u Ø " u (Ø " u " y (Ø " u " y " x (Ø " x " y " u (Ø
Вопросы для самопроверки и упражнения.
1. Проиллюстрировать справедливость соотношений (4.16) и (4.17) для предикатов
2. Получить ПНФ следующих предикатных формул: а) $ x " y б) ($ x " y в) Ø($ x " z г) ($ x " z д) (" x $ y " z е) Ø(" x " y " z Ø ж) (" x " y Ø з) Ø" x $ y Ø и) (Ø$ y Ø к) Ø(" x " y Ø
ВОПРОСЫ КОЛЛОКВИУМА “ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ ЛОГИКУ”.
1. Определение высказывания. Сложные высказывания.
2. Определение логической формулы.
3. Метод установления эквивалентности формул.
4. Основные схемы логически правильных рассуждений.
5. Определение функции алгебры логики.
6. Таблицы истинности унарной и бинарной логических операций.
7. Инфиксная и префиксная формы задания логической функции.
8. Полнота и базис (определения) в булевой алгебре.
9. Классы Поста (определения).
10. Полином Жегалкина (способы построения).
11. Критерий полноты Поста-Яблонского.
12. Свойства функций Шеффера и Вебба (Пирса).
13. Основные эквивалентные соотношения (законы) булевой алгебры.
14. Определение СДНФ (СКНФ).
15. Приведение к ДНФ (КНФ).
16. Алгоритмы перехода от табличного задания булевой функции к СДНФ (СКНФ).
17. Метод Блейка-Порецкого упрощения СДНФ.
18. Указать все булевы функции от 2-х переменных в классах Т 0, Т 1, L, S, M.
19. Алгебра логики (определение).
20. Способы проверки правильности рассуждений.
21. Методы построения таблиц истинности для функций алгебры логики от n переменных.
22. Принцип двойственности в булевой алгебре.
23. Изоморфизм булевых алгебр (определение).
24. Соответствия между предикатами, отношениями и функциями.
25. Изоморфизм булевых алгебр множеств и двоичных векторов.
26. Условия гомоморфизма в алгебре множеств и булевой алгебры.
27. Изоморфизм булевых алгебр множеств и логических функций.
28. Определение n -местного предиката.
29. Кванторы.
30. Интерпретация формул логики предикатов.
31. Определение модели в логике предикатов.
32. Истинность, ложность или выполнимость формул логики предикатов.
33. Эквивалентные соотношения в логике предикатов.
34. Префиксные нормальные формы (ПНФ) в логике предикатов. Список литературы
|
||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.132.214.111 (0.011 с.) |

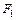 и
и 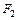 эквивалентны, то
эквивалентны, то 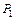 (x)&
(x)& 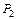 (x))~(" x
(x))~(" x 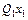
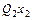 ...
... 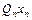 F, где
F, где 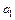 и
и 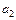 . Что касается (4.17), то здесь требуется, чтобы в левой части хотя бы один предикат выполнялся для всех a Î M; правой части достаточно, чтобы один предикат был истинен там, где ложен другой. В этих рассуждениях, по существу, содержатся доказательства справедливости (4.16) и (4.17).
. Что касается (4.17), то здесь требуется, чтобы в левой части хотя бы один предикат выполнялся для всех a Î M; правой части достаточно, чтобы один предикат был истинен там, где ложен другой. В этих рассуждениях, по существу, содержатся доказательства справедливости (4.16) и (4.17).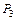 (x, y, u)).
(x, y, u)).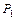 (x) – “ x – четное число” и
(x) – “ x – четное число” и 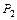 (x) – “ x – нечетное число” и недопустимость замены в (4.16) и (4.17) символа ® на ~, т.е. показать, что для данных предикатов указанные соотношения справедливы лишь в одну сторону.
(x) – “ x – нечетное число” и недопустимость замены в (4.16) и (4.17) символа ® на ~, т.е. показать, что для данных предикатов указанные соотношения справедливы лишь в одну сторону. (y, z);
(y, z);


