
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Булева алгебра и теория множеств.Содержание книги Поиск на нашем сайте
Примеры булевых алгебр: ( ( (b(U); Ç,È,Ø) – булева алгебра множеств над U; (b(U ¢); Ç,È,Ø) – булева алгебра множеств над U ¢, U ¢Ì U; ( Для любых векторов а) б) в)
Теорема 1.6.1. Если | U |= n, то булева алгебра множеств (b(U); Ç,È,Ø) изоморфна булевой алгебре двоичных векторов ( Теорема 1.6.2. Если | U |=2 m, то булева алгебра множеств (b(U); Ç,È,Ø) изоморфна булевой алгебре функций ( Взаимный изоморфизм данных булевых алгебр выполняется, если | U |= n =2 m. В этом случае |b(U)|=| Изоморфизм булевых алгебр широко используется в компьютерных вычислениях, например, вместо выполнения операций над множествами или логическими функциями используют их изоморфные аналоги – легко реализуемые на компьютере поразрядные операции над двоичными векторами.
Пример 1. Показать на примере конкретных множеств A, B Í U изоморфизм между булевыми алгебрами множеств (b(U); Ç,È,Ø), где | U |=4, и булевой алгеброй двоичных векторов длины 4 (
Пусть U ={ a, b, c, d }. Тогда b(U)={Æ, { a }, { b }, { c }, { d }, { a, b },...,{ a, b, c },...,{ a, b, c, d }};
|b(U)|=| Если булевы алгебры (b(U); Ç,È,Ø) и ( 1) существует взаимно однозначное соответствие – отображение Г:b(U)® 2) для отображение Г:b(U)® а) Г(A Ç B)= Проиллюстрируем выполнение всех условий изоморфизма заданных алгебр на примере двух конкретных множеств, например, A ={ b, c } и B ={ a, c, d }: 1) взаимно однозначное соответствие: Г(A)=(0110)= 2) условие гомоморфизма: а) Г(A Ç B)=Г({ b, c }Ç{ a, c, d })=Г({ c })=(0010)=(0110)&(1011)=
б) Г(A È B)=Г({ b, c }È{ a, c, d })=Г({ a, b, c, d })=(1111)=(0110)Ú(1011) = в) Г( Таким образом, алгебры (b(U); Ç,È,Ø) и (
Пример 2. Используя изоморфизм булевых алгебр множеств и двоичных векторов, выполнить булевы операции: 1) над множествами A ={ a, d, e }, B ={ b, c, d }; 2) над двоичными векторами t=(100110) и s=(010011).
Булевы алгебры множеств (b(U); Ç,È,Ø) и двоичных векторов ( 1) Пусть | Г(A)=Г({ a, d, e })=(10011)= Г(B)=Г({ b, c, d })=(01110)= b. Тогда: а) Г(A Ç B)= Но вектору (00010) соответствует множество { d }: Г-1((00010))={ d }. Таким образом, A Ç B ={ d }. б) Г(A È B)= в) Г( Изоморфизм булевых алгебр множеств и двоичных векторов позволяет заменить теоретико-множественные операции над множествами поразрядными логическими операциями над двоичными векторами. 2) Длина n заданных двоичных векторов t=(100110) и s=(010011) равна 6. Поэтому пусть | Выполним операции (&,Ú,Ø) над векторами, используя изоморфизм алгебр Г: Г(t)=Г((100110))={ f, k, m }= C; Г(s)=Г((010011))={ g, m, q }= D. Тогда: а) Г(t&s)= C Ç D ={ f, k, m }Ç{ g, m, q }={ m }. Но множеству { m } соответствует вектор (000010): Г-1({ m })= (000010). Таким образом, t&s=(100110)&(010011)=(000010). б)Г(tÚs)= C È D ={ f, k, m }È{ g, m, q }={ f, g, k, m, q }, но Г-1({ f, g, k, m, q })= (110111). Таким образом, tÚs=(100110)Ú(010011)=(110111).
Пример 3. Проиллюстрировать изоморфизм между булевыми алгебрами множеств (b(U); Ç,È,Ø) и логических функций (
Пусть | U |=2 m при m =2; U ={ a, b, c, d }. Изоморфизм данных алгебр означает: 1. Между логическими функциями двух переменных из
2. Для отображения Г: а) Г(f & g)= В силу изоморфизма этих алгебр справедливо и обратное: а) Г-1( Однако из-за взаимной однозначности Г достаточно показать справедливость лишь первых трех равенств. Пусть
Таблица 1.6.1 | ||||||||||||
| Элемент множества U | x 1 | x 2 | f | g | f & g | f Ú g | 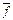
| ||||||
| a | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||
| b | 0 | 1 | 0 | 1 | 0 | 1 | 1 | ||||||
| c | 1 | 0 | 1 | 1 | 1 | 1 | 0 | ||||||
| d | 1 | 1 | 0 | 0 | 0 | 0 | 1 | ||||||
Функции f и g, соответствующие множествам 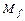 и
и 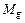 при взаимно однозначном отображении Г (характеристические функции для
при взаимно однозначном отображении Г (характеристические функции для 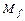 и
и 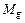 ), определены таблицами истинности 1.6.1. В крайнем левом столбце таблицы 1.6.1 перечислены элементы множества U ={ a, b, c, d }, являющиеся, по существу, обозначениями всех возможных наборов двух переменных {(00),(01),(11)}. Множества
), определены таблицами истинности 1.6.1. В крайнем левом столбце таблицы 1.6.1 перечислены элементы множества U ={ a, b, c, d }, являющиеся, по существу, обозначениями всех возможных наборов двух переменных {(00),(01),(11)}. Множества 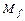 и
и 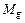 представляют собой единичные множества функций f и g соответственно, т.е. множества наборов, на которых эти функции равны единице. Тогда (см. табл. 1.6.1):
представляют собой единичные множества функций f и g соответственно, т.е. множества наборов, на которых эти функции равны единице. Тогда (см. табл. 1.6.1):
1) Г(f)= 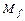 ={ a, c }, Г(g)=
={ a, c }, Г(g)= 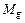 ={ b, c } и, наоборот, Г-1(
={ b, c } и, наоборот, Г-1(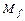 )= f и Г-1(
)= f и Г-1(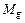 )= g;
)= g;
2) Г(f & g)= 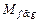 ={ c }={ a, c }Ç{ b, c }=
={ c }={ a, c }Ç{ b, c }= 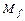 Ç
Ç 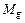 ,
,
Г(f Ú g)= 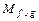 ={ a, b, c }={ a, c }È{ b, c }=
={ a, b, c }={ a, c }È{ b, c }= 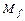 È
È 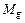 ,
,
Г(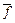 )=
)= 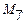 ={ b, d }= U \{ a, c }= U \
={ b, d }= U \{ a, c }= U \ 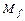 =
= 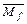 .
.
Пример 4. Выполнить булевы операции над логическими функциями трех переменных 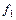 и
и 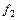 , используя изоморфизм булевых алгебр логических функций и двоичных векторов, если:
, используя изоморфизм булевых алгебр логических функций и двоичных векторов, если:
1) 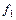 и
и 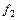 определены таблицами истинности в табл. 1.6.2
определены таблицами истинности в табл. 1.6.2
2) 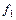 и
и 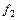 определены своими СДНФ:
определены своими СДНФ:
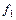
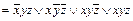 ,
,
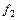
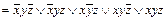 .
.
Изоморфизм булевых алгебр логических функций (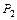 (m); &,Ú,Ø) и двоичных векторов (
(m); &,Ú,Ø) и двоичных векторов (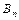 ; &,Ú,Ø) позволяет переходить от операций над функциями к операциям над двоичными векторами и обратно при выполнении условия: 2 m = n. Поэтому функциям трех переменных (m =3) соответствуют вектора длины n =8. Установим взаимно однозначное соответствие Г:
; &,Ú,Ø) позволяет переходить от операций над функциями к операциям над двоичными векторами и обратно при выполнении условия: 2 m = n. Поэтому функциям трех переменных (m =3) соответствуют вектора длины n =8. Установим взаимно однозначное соответствие Г: 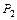 (3)®
(3)® 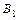 и выполним необходимые операции, используя изоморфизм булевых алгебр.
и выполним необходимые операции, используя изоморфизм булевых алгебр.
1)Зафиксировав последовательность рассмотрения всех возможных наборов значений переменных, например, как это указано в табл. 1.6.2, установим взаимно однозначное соответствие Г: 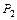 (3)®
(3)® 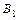 следующим образом:
следующим образом:
для функции f, представленной таблицей истинности, в соответствующем ей векторе 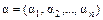 i -я компонента
i -я компонента 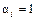 , если для f i -й набор значений переменных является единичным, т.е. функция на этом наборе принимает значение f =1, и
, если для f i -й набор значений переменных является единичным, т.е. функция на этом наборе принимает значение f =1, и 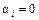 – в противном случае.
– в противном случае.
|
Таблица 1.6.2 | |||||||
 x 1 x 1
| x 2 | x 3 | f 1 | f 2 | f 1& f 2 | f 1Ú f 2 | f 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Тогда:
Г(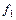 )=(00011011)=
)=(00011011)= 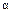 , Г(
, Г(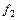 )=(00110111)=b.
)=(00110111)=b.
Выполним операции (&,Ú,Ø) над функциями 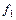 и
и 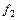 , используя изоморфизм булевых алгебр Г:
, используя изоморфизм булевых алгебр Г: 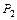 (3)®
(3)® 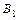 :
:
а) Г(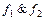 )=
)= 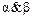 =(00011011)&(00110111)=(00010011).
=(00011011)&(00110111)=(00010011).
Но вектору (00010011) соответствует функция 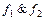 :
:
Г-1((00010011))= 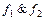 ,
,
таблица истинности которой представлена в табл. 1.6.2.
б) Г(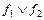 )=
)= 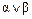 =(00011011)Ú(00110111)=(00111111).
=(00011011)Ú(00110111)=(00111111).
Но Г-1((00111111))= 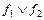 (см. табл. 1.6.2).
(см. табл. 1.6.2).
в) Г(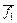 )=
)= 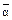 =
= 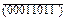 =(11100100).
=(11100100).
Г-1((11100100))= 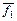 (см. табл. 1.6.2).
(см. табл. 1.6.2).
2) Определим последовательность всех возможных элементарных конъюнкций всех переменных (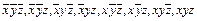 ) и установим взаимно однозначное соответствие Г:
) и установим взаимно однозначное соответствие Г: 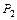 (3)®
(3)® 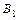 следующим образом:
следующим образом:
|
|
для функции f, представленной СДНФ, в соответствующей ей векторе 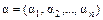 i -я компонента
i -я компонента 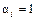 , если в СДНФ f имеется i -я конъюнкция, и
, если в СДНФ f имеется i -я конъюнкция, и 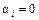 – в противном случае.
– в противном случае.
Тогда:
Г(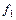 )=Г(
)=Г(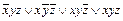 )=(00011011)=
)=(00011011)= 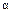 ,
,
Г(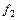 )=(
)=(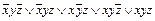 )=(00110111)= b.
)=(00110111)= b.
Выполним операции (&,Ú,Ø) над функциями 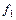 и
и 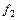 , используя изоморфизм булевых алгебр Г:
, используя изоморфизм булевых алгебр Г: 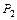 (3)®
(3)® 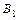 :
:
а) Г(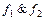 )=
)= 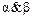 =(00011011)&(00110111)=(00010011).
=(00011011)&(00110111)=(00010011).
Но вектору (00010011) соответствует функция, СДНФ которой
Г-1((00010011)) 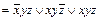 .
.
Таким образом, 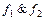
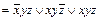 .
.
б) Г(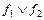 )=
)=  =(00011011)Ú(00110111)=(00111111).
=(00011011)Ú(00110111)=(00111111).
Но Г-1((00111111)) 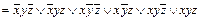 .
.
Таким образом, 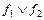
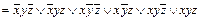 .
.
в) Г(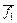 )=
)= 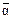 =
= 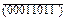 =(11100100).
=(11100100).
Но Г-1((11100100)) 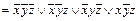 .
.
Таким образом, 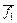
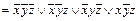 .
.
Пример 5. Выполнить операции объединения и пересечения над множествами A, B Í U из примера 2, используя изоморфизм булевых алгебр множеств и логических функций.
Изоморфизм булевых алгебр позволяет переходить от операций над множествами к операциями над функциями и обратно. Изоморфизм булевых алгебр требует выполнения условия: | U |=2 m. Поэтому для выполнения операции над A ={ a, d, e }, B ={ b, c, d } рассмотрим изоморфные алгебры: (b(U); Ç,È,Ø) и (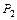 (3); &,Ú,Ø).
(3); &,Ú,Ø).
Пусть U ={ a, b, c, d, e, h, k, l }; взаимно однозначное соответствие Г:b(U)® 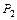 (3) установим так, как показано в табл. 1.6.3, где в крайнем правом столбце перечислены элементы множества U. Функции f и g, соответствующие множествам A, B, а также их конъюнкция, дизъюнкция, отрицание даны таблицами истинности (табл. 1.6.3).
(3) установим так, как показано в табл. 1.6.3, где в крайнем правом столбце перечислены элементы множества U. Функции f и g, соответствующие множествам A, B, а также их конъюнкция, дизъюнкция, отрицание даны таблицами истинности (табл. 1.6.3).
Тогда:
Г(A & B)= f & g, но Г-1(f & g)= 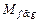 ={ d }, т.е. A & B ={ d };
={ d }, т.е. A & B ={ d };
Г(A Ú B)= f Ú g, но Г-1(f Ú g)= 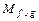 ={ a, b, c, d, e }, т.е. A Ú B ={ a, b, c, d, e }.
={ a, b, c, d, e }, т.е. A Ú B ={ a, b, c, d, e }.
|
Таблица 1.6. 3 | |||||||
| x | y | z | f | g | f & g | f Ú g | Элемент множества U |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | a |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | b |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | c |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | d |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | e |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | h |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | k |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | l |
Вопросы для самопроверки и упражнения.
1. Показать изоморфизм булевых алгебр (b(U); Ç,È,Ø) и (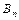 ; &,Ú,Ø) на примере A, B Í U, если:
; &,Ú,Ø) на примере A, B Í U, если:
а) A ={2,4,6}, B ={1,2,3,6}, U ={1,2,3,4,5,6};
б) A ={ a, c, d, f }, B ={ b, c, e, f }, U ={ a, b, c, d, e, f };
в) A ={1,3,4,6}, B ={2,3,5,6}, U ={1,2,3,4,5,6};
г) A ={ c, d, e }, B ={ a, b, c, f }, U ={ a, b, c, d, e, f };
2. Показать изоморфизм булевых алгебр (b(U); Ç,È,Ø) и (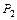 (m); &,Ú,Ø) на примере A, B Í U, если:
(m); &,Ú,Ø) на примере A, B Í U, если:
а) A ={2,4,6}, B ={1,2,3,6}, U ={1,2,3,4,5,6,7,8};
б) A ={1,3,4,6,8}, B ={2,3,5,6,7}, U ={1,2,3,4,5,6,7,8};
в) A ={ a, c, d, h }, B ={ b, c, d, e, h }, U ={ a, b, c, d, e, f, g, h };
г) A ={ c, d, e, g }, B ={ a, c, d, g, h }, U ={ a, b, c, d, e, f, g, h };
3. Задать множества A, B Í U. Выполнить операции {Ç,È,Ø} над множествами A, B, используя изоморфизм булевых алгебр множеств (b(U); Ç,È,Ø) и:
|
|
а) двоичных векторов (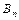 ; &,Ú,Ø);
; &,Ú,Ø);
б) логических функций (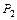 (m); &,Ú,Ø).
(m); &,Ú,Ø).
ЛОГИКА ПРЕДИКАТОВ.
Основные понятия.
Предикат P ( ,
,  ,...,
,...,  ) является функцией типа P:
) является функцией типа P: 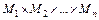 ® B, где множества
® B, где множества 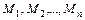 называются предметными областями предиката;
называются предметными областями предиката;  ,
,  ,...,
,...,  – предметными переменными,
– предметными переменными,  Î
Î 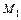 ,
,  Î
Î 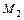 ,...,
,...,  Î
Î 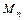 ; B ={И,Л} или {1,0}. Если предикатные переменные принимают значения на одном множестве, то P:
; B ={И,Л} или {1,0}. Если предикатные переменные принимают значения на одном множестве, то P: 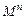 ® B.
® B.
Соответствия между предикатами, отношениями и функциями:
1. Для любых M и n существует взаимно однозначное соответствие между n -местными отношениями R Í 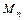 и n -местными предикатами P (
и n -местными предикатами P ( ,
,  ,...,
,...,  ), P:
), P: 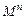 ® B:
® B:
- каждому n -местному отношению R соответствует предикат P ( ,
,  ,...,
,...,  ) такой, что P (
) такой, что P ( ,
,  ,...,
,..., 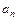 )=1, если и только если (
)=1, если и только если ( ,
,  ,...,
,..., 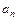 )Î R;
)Î R;
- всякий предикат P ( ,
,  ,...,
,...,  ) определяет отношение R такое, что (
) определяет отношение R такое, что ( ,
,  ,...,
,..., 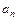 )Î R, если и только если P (
)Î R, если и только если P ( ,
,  ,...,
,..., 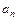 )=1.
)=1.
При этом R задает область истинности предиката P.
2. Всякой функции f ( ,
,  ,...,
,...,  ), f:
), f: 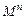 ® M, соответствует предикат P (
® M, соответствует предикат P ( ,
,  ,...,
,...,  ,
, 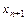 ), P:
), P: 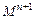 ® B, такой, что P (
® B, такой, что P ( ,
,  ,...,
,..., 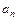 ,
, 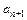 )=1, если и только если f (
)=1, если и только если f ( ,
,  ,...,
,..., 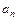 )=
)= 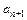 .
.
Выражение P ( ,
,  ,...,
,..., 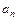 ) будем понимать как высказывание “ P (
) будем понимать как высказывание “ P ( ,
,  ,...,
,..., 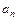 )=1” или “ P (
)=1” или “ P ( ,
,  ,...,
,..., 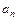 ) истинно”, а выражение P (
) истинно”, а выражение P ( ,
,  ,...,
,...,  ) – как переменное высказывание, истинность которого определяется подстановкой элементов множества M вместо переменных
) – как переменное высказывание, истинность которого определяется подстановкой элементов множества M вместо переменных  ,
,  ,...,
,...,  . При этом будем также называть P (
. При этом будем также называть P ( ,
,  ,...,
,...,  ) логической (двоичной) переменной, в отличие от
) логической (двоичной) переменной, в отличие от  ,
,  ,...,
,...,  – предметных (нелогичных) переменных.
– предметных (нелогичных) переменных.
Из предикатов как высказываний можно образовывать составные высказывания – формулы логики предикатов.
Для обозначения двухместных предикатов помимо префиксной записи P ( ,
,  ) используется нередко инфиксная запись
) используется нередко инфиксная запись  P
P  .
.
Пример 1. Каким отношениям и функциям соответствуют следующие предикаты, определенные на множестве натуральных чисел:
1. Предикат тождества E: 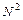 ® B: E (
® B: E ( ,
,  )=1Û
)=1Û  =
=  .
.
2. Предикат порядка Q: 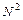 ® B: Q (
® B: Q ( ,
,  )=1Û
)=1Û  £
£  .
.
3. Предикат делимости D: 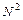 ® B: D (
® B: D ( ,
,  )=1Û
)=1Û  делится на
делится на  .
.
4. Предикат суммы S: 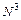 ® B: S (
® B: S ( ,
,  ,
, 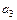 )=1Û
)=1Û  +
+  =
= 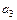 .
.
5. Предикат произведения П: 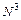 ® B: П (
® B: П ( ,
,  ,
, 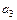 )=1Û
)=1Û  ×
×  =
= 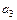 .
.
1. Двухместному предикату тождества E – “  =
=  ” взаимно однозначно соответствуют:
” взаимно однозначно соответствуют:
а) двухместное отношение 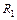 – “быть равным”,
– “быть равным”, 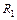 Í
Í 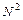 : (
: ( ,
,  )Î
)Î 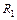 Û E (
Û E ( ,
,  )=1;
)=1;
б) одноместная функция (операция) тождества 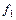 (
( )=
)=  , а именно:
, а именно: 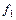 (x)= x, f: N ® N.
(x)= x, f: N ® N.
2. Двухместному предикату порядка Q – “  £
£  ” взаимно однозначно соответствует двухместное отношение
” взаимно однозначно соответствует двухместное отношение 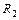 – “быть не больше”,
– “быть не больше”, 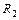 Í
Í 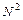 : (
: ( ,
,  )Î
)Î 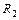 Û Q (
Û Q ( ,
,  )=1;
)=1;
3. Двухместному предикату делимости D – “  делится на
делится на  ” взаимно однозначно соответствует двухместное отношение
” взаимно однозначно соответствует двухместное отношение 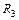 – “делиться”,
– “делиться”, 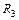 Í
Í 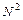 : (
: ( ,
,  )Î
)Î 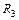 Û D (
Û D ( ,
,  )=1;
)=1;
4. Трехместному предикату суммы S – “  +
+  =
=  ” взаимно однозначно соответствуют:
” взаимно однозначно соответствуют:
а) трехместное отношение 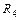 Í
Í 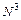 : (
: ( ,
,  ,
, 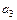 )Î
)Î 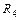 Û S (
Û S ( ,
,  ,
, 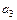 )=1;
)=1;
б) двухместная функция (операция арифметики) – сложение 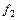 (
( ,
,  )=
)=  , а именно:
, а именно:  +
+  =
=  .
.
5. Трехместному предикату произведения П – “  ×
×  =
=  ” взаимно однозначно соответствуют:
” взаимно однозначно соответствуют:
а) трехместное отношение 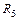 Í
Í 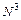 : (
: ( ,
,  ,
, 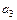 )Î
)Î 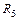 Û П (
Û П ( ,
,  ,
, 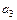 )=1;
)=1;
б) двухместная функция (операция арифметики) – умножение 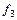 (
( ,
,  )=
)=  , а именно:
, а именно:  ×
×  =
=  .
.
Взаимная однозначность соответствия между S и 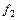 (П и
(П и 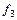 ) обусловлена выполнением для предиката S (П) условия: для каждой системы элементов
) обусловлена выполнением для предиката S (П) условия: для каждой системы элементов  ,
,  Î N существует единственный элемент
Î N существует единственный элемент 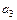 Î N такой, что S (
Î N такой, что S ( ,
,  ,
, 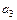 )=1 (соответственно, для П (
)=1 (соответственно, для П ( ,
,  ,
, 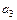 )=1).
)=1).
|
|
Кванторы.
Пусть P (x) – предикат, определенный на M, т.е. x Î M.
Высказывание “для всех x из M P (x) истинно” обозначается " x P (x); знак " x называется квантором общности. Высказывание “существует такой x из M, что P (x) истинно” обозначается $ x; знак $ x называется квантором существования.
Переход от P (x) к " x P (x) или $ x P (x) называется связыванием переменной x, или навешиванием квантора на переменную x (или на предикат P), или квантификацией переменной P.
Переменная, на которую навешен квантор, называется связанной, несвязанная квантором переменная называется свободной.
Выражение, на которое навешивается квантор " x или $ x, называется областью действия квантора; все вхождения переменной x в это выражение я<
|
| Поделиться: |

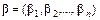 :
: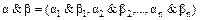 , где
, где 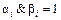 , если
, если 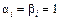 и
и 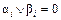 в любом другом случае;
в любом другом случае;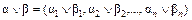 , где
, где 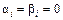 и
и 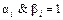 в любом другом случае;
в любом другом случае;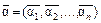 , где
, где 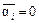 , если
, если 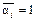 в противном случае.
в противном случае.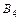 ={(0000), (0001), (0010),..., (1111)};
={(0000), (0001), (0010),..., (1111)};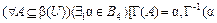 ) = A ].
) = A ].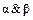 , б) Г(A È B)=
, б) Г(A È B)= 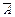 )=
)= 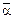 .
.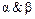 ;
;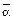 .
.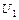 |= n =5 и
|= n =5 и 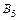 ; &,Ú,Ø). Выполним операции над множествами {Ç,È,Ø}, используя изоморфизм этих алгебр Г:b(
; &,Ú,Ø). Выполним операции над множествами {Ç,È,Ø}, используя изоморфизм этих алгебр Г:b(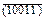 =(01100), но Г-1((01100))={ b, c }, откуда
=(01100), но Г-1((01100))={ b, c }, откуда 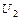 |= n =6 и
|= n =6 и 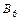 ®b(
®b(
 в) Г(t)=
в) Г(t)= 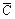 =
= 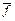 )=
)= 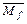 .
.


