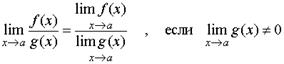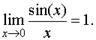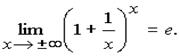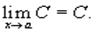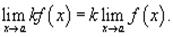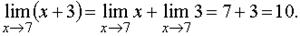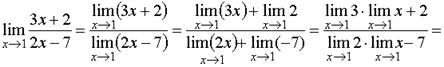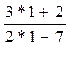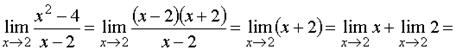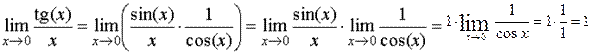Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции в точке и на бесконечностиСодержание книги
Поиск на нашем сайте
Определение предела функции в точке. Число b называется пределом функции у=f(x) при x стремящемся к a, если для любого положительного числа e можно указать такое положительной число d= Обозначение предела. Если b есть предел функции f(x) при x стремящемся к a, то записывают это так:
Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство | f(x) – b | < e. Запись этого факта:
Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство | f(x) – b | < e. Записывается это так:
Геометрический смысл равенства состоит в следующем: прямая у = b является горизонтальной асимптотой графика функции у = f(х) (и в положительном, и в отрицательном направлении).
Теоремы о пределах ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля ТЕОРЕМА 4. Предел постоянной величины равен самой постоянной величине:
ТЕОРЕМА 5. Постоянный коэффициент можно выносить за знак предела:
Замечательные пределы Первый замечательный предел равен
Второй замечательный равен
Вычисление пределов функции, раскрытие неопределенностей Пример 1. Найти предел
Пример 2. Найти предел
Пример 3. Найти предел Это преобразование справедливо при всех значениях x, отличных от 2, поэтому в соответствии с определением предела можем написать
Вычисление пределов с помощью теоремы о первом замечательном пределе Пример. Найти предел
|
||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.197 (0.009 с.) |

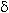 (
( ), что для всех x, отличных от a и удовлетворяющих неравенству | x-a |<d, имеет место неравенство |f(x)-b|<d.
), что для всех x, отличных от a и удовлетворяющих неравенству | x-a |<d, имеет место неравенство |f(x)-b|<d.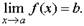
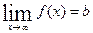
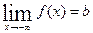
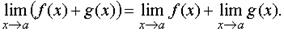 ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть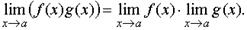 ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть