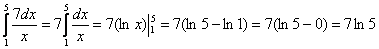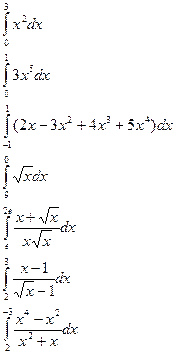Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Определенный интегралСодержание книги
Поиск на нашем сайте
Основные свойства и методы вычисления
Пусть на отрезке [ a, b ] (b > a) задана непрерывная функция y = f (x), принимающая на этом отрезке неотрицательные значения:
Для решения этой задачи разделим произвольным образом основание AD фигуры точками x 0 = a, x 1 , x 2 , …, xn -1 = a, xn = b на n частей [ x 0 , x 1], [ x 1 , x 2], …, [ xi -1 , xi ], …, [ xn -1 , xn ]; символом S n равно площади ступенчатой фигуры, образованной прямоугольниками Pi, i = 1,2,…, n; на левом рисунке эта площадь заштрихована. S ступ не равна искомой площади S, она только даёт некоторое приближение к S.
Если существует (конечный) предел последовательности интегральных сумм Sn при
Свойства определенного интеграла
1. Если b=a, то
2. если b < a, то
3.
4. 5.
6. Интегрирование неравенств. Если в любой точке Геометрический смысл определённого интеграла
ABCD, ограниченной снизу отрезком [ a, b ], слева и справа - прямыми x = a и x = b, сверху – функцией y = f (x). Вычисление определённого интеграла. Формула Ньютона-Лейбница
то Пример 1. применения формулы Ньютона-Лейбница: Пример 2. Вычислить определенный интеграл Решение: Пример 3.
Вычислить интегралы:
|
|||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.209.144 (0.006 с.) |

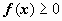 при
при 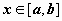 . Требуется определить площадь фигуры S, ограниченной снизу отрезком [ a, b ], слева и справа - прямыми x = a и x = b, сверху – функцией y = f (x). Эта фигура называется криволинейной трапеции ABCD
. Требуется определить площадь фигуры S, ограниченной снизу отрезком [ a, b ], слева и справа - прямыми x = a и x = b, сверху – функцией y = f (x). Эта фигура называется криволинейной трапеции ABCD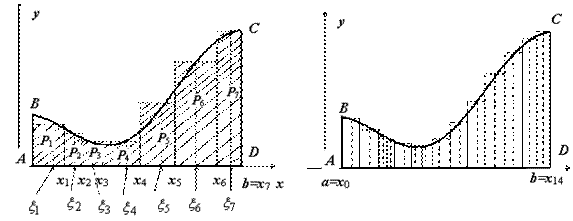
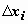 будем обозначать длину i -го отрезка:
будем обозначать длину i -го отрезка: 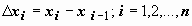 . На каждом из отрезков [ xi -1 , xi ] выберем произвольную точку
. На каждом из отрезков [ xi -1 , xi ] выберем произвольную точку  , найдём
, найдём 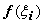 , вычислим произведение
, вычислим произведение  (это произведение равно площади прямоугольника Pi с основанием [ xi -1 , xi ] и высотой
(это произведение равно площади прямоугольника Pi с основанием [ xi -1 , xi ] и высотой 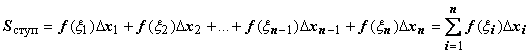 .
.  Обозначим через длину наибольшего частичного отрезка
Обозначим через длину наибольшего частичного отрезка  , не зависящий ни от способа разбиения отрезка [ a, b ] на части [ xi -1 , xi ], ни от выбора точек
, не зависящий ни от способа разбиения отрезка [ a, b ] на части [ xi -1 , xi ], ни от выбора точек  .
.  Функция f (x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.
Функция f (x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования. Кратко определение иногда записывают так:
Кратко определение иногда записывают так: 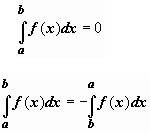
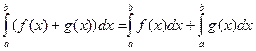


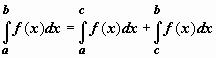 6. Если функция y= f(x ) интегрируема на отрезке [a,b], то для любой точки с внутри отрезка верно равенство
6. Если функция y= f(x ) интегрируема на отрезке [a,b], то для любой точки с внутри отрезка верно равенство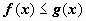 , и функции f (x), g (x) интегрируемы по отрезку [ a, b ], то
, и функции f (x), g (x) интегрируемы по отрезку [ a, b ], то 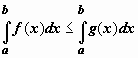 .
. 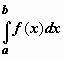 Если f (x) >0 на отрезке [ a, b ], то равен площади криволинейной трапеции
Если f (x) >0 на отрезке [ a, b ], то равен площади криволинейной трапеции Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции
Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции 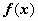 ,
,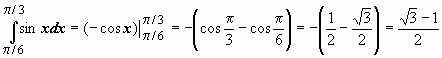 .
.