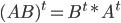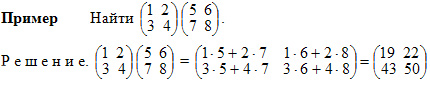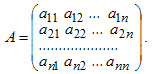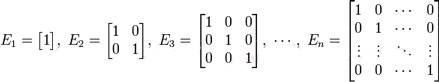Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменной в определённом интегралеСодержание книги
Поиск на нашем сайте
Теорема. Пусть функция
1.определена, непрерывно дифференцируема и монотонна на отрезке
2.
3.
Пример 4.
Пример Вычислить определенный интеграл Пример Вычислить определенный интеграл Вычисление площадей плоских фигур Пример 1. Найти площадь фигуры, ограниченной линиями
Рисунок 2 Решение:
(0;2) – вершина
Найдём пределы интегрирования.
Ответ: Пример 2. Вычислить площадь фигуры, ограниченной линиями Выполним чертеж (уравнение
На отрезке
Ответ: Пример 3. Вычислить площадь фигуры, ограниченной линиями a) f (x) = 2 х – х 2 и осью абсцисс Решение: График функции f(x) = 2x - х2 парабола. Вершина: (1; 1).
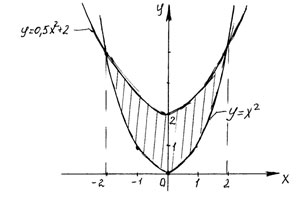
Ответ: Пример 4. Найти площадь фигуры, ограниченной линиями Решение: График функции
Функция
Пределы интегрирования указаны в таблицах значений функций.
Ответ:
ТЕМА 5. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ Общая характеристика матрицы Матрицей размерности m*n называется таблица чисел (элементов), содержащая m строк и n столбцов.
В алгебраических выражениях часто используются специального вида матрицы: Θ — нулевая D — диагональная E — единичная Если в матрице А переставить соответствующие строки и столбцы местами, то получится матрица Ат, которую называют транспонированной матрицей А.
Пример:
Если число строк и столбцов матрицы совпадает и равно n, то матрица называется квадратной n-го порядка.Две матрицы А и В одинаковой размерности равны, если все соответствующие элементы матриц равны.
Действия над матрицами Умножение матрицы на число. Любую матрицу можно умножить на любое число, при этом все элементы матрицы умножаются на это число.
Сложение матриц. Две матрицы А и В одинаковой размерности можно сложить, при этом все соответветствующие элементы матриц складываются.
Свойства линейных операций
Умножение матриц Две матрицы можно умножить, если число строк второй матрицы равно числу столбцов первой матрицы. При умножении матриц получается матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
Элементы матрицы произведения С = АВ находятся по формуле:
где l — число строк второй и число столбцов первой матриц.
Свойства умножения матриц:
Пример. Произведите умножение матриц
Всегда: строки первой матрицы умножаются на столбцы второй матрицы, то есть никогда не будет ситуации когда необходимо будет умножать столбцы первой на строки второй! Важно: матрицы при умножении нельзя менять местами!!! — результат умножения будет другим
Обратная матрица Пусть имеется квадратная матрица n-го порядка
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.76.151 (0.006 с.) |

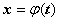
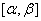
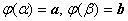 функция
функция 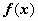 непрерывна на отрезке [ a, b ]
непрерывна на отрезке [ a, b ]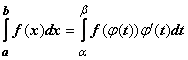 Тогда
Тогда 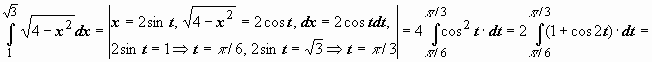
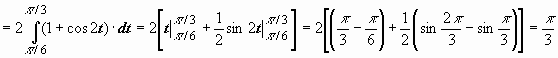
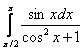
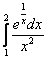
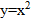 ,
, 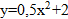 .
.
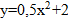 – парабола, вершина (m,n).
– парабола, вершина (m,n).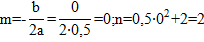
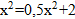
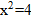

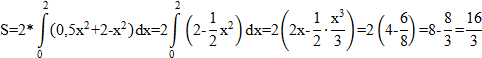
 (кв.ед).
(кв.ед).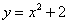 ,
, 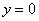 ,
, 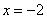 ,
, 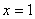 .
.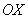 ):
):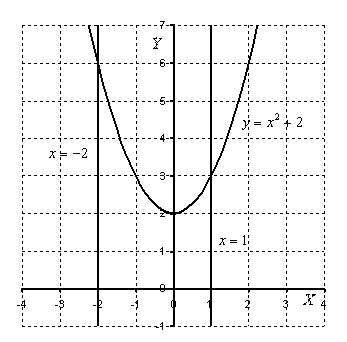
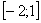 график функции
график функции 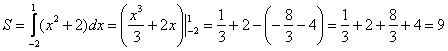
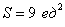
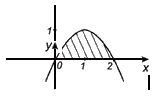
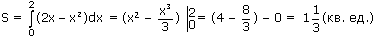
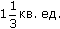
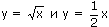
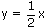 – прямая.
– прямая.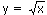 является обратной функции y = х 2 на промежутке [0; +∞).
является обратной функции y = х 2 на промежутке [0; +∞).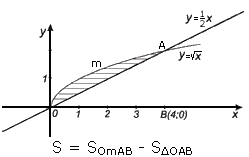
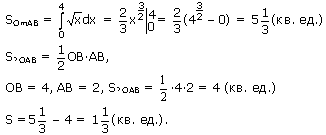
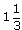 (кв. ед)
(кв. ед)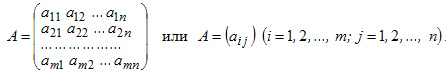
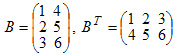
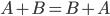
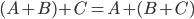
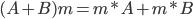
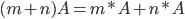
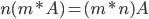
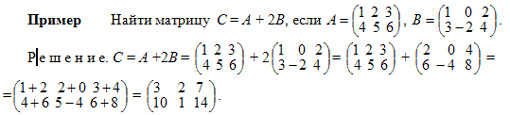
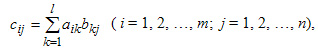
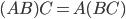
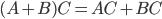
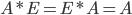 (где Е — единичная матрица)
(где Е — единичная матрица)