
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки разрыва функции и их классификация
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х= х0 – точка разрыва функции y=f(x), то в ней не выполняется хотя бы одно их 3-х условий первого определения непрерывности функции. Все точки разрыва разделяются на точки разрыва первого и второго рода Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
При этом: 1. если А=В, то точка х0 называется точкой устранимого разрыва 2. если А# В, то точка х0 называется точкой конечного разрыва Величину | A- B | называют скачком функции в точке разрыва первого рода Точки устранимого разрыва и конечного скачка называются точками разрыва 1–го рода. Их отличительным признаком является существование конечных односторонних пределов. Точка разрыва х0 называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, или равен бесконечности Пример 9. Найти точки разрыва функции, если они существуют, б) найти односторонние пределы в точках разрыва и установить тип точек разрыва функции f(x)=2 x/(3+x) Решение: Функция f(x)=2 x/(3+x) не определена в точке х=-3, значит это точка разрыва. Найдем односторонние пределы в этой точке. Сначала найдем односторонние пределы функции Пример 10. Найти точки разрыва функции и определить их тип f(x)= (x2 – 25)/(x-5) Решение: Область определения функции (- ¥,5)È (5, +¥). Точка х = 5 – точка разрыва Lim (x-5)(x+5)/(x -5)= lim (x+5) при х → 5 Lim (x+5) = 10 при x → 5-0 Lim (x+5) = 10 при x → 5+0 Т.е. односторонние пределы равны и х = 5 – точка устранимого разрыва 1 рода Пример 11. Исследовать функцию на непрерывность и определить вид точек разрыва У= 1/х Решение: Область определения функции (- ¥,0)È (0, +¥). Точка х = 5 – точка разрыва Рассмотрим односторонние пределы Lim 1/x = - ¥ при х → 0-0 Lim 1/x = + ¥ при х → 0+0 Т.е. х=0 – точка разрыва 2 рода Пример 12. Исследовать функцию на непрерывность и определить вид точек разрыва
f(x) = x / (1+x2) Решение: Lim x/(1+x2) = - ¥ при х = -1-0 Lim x/(1+x2) = + ¥ при х = -1+0 Т.е. х=-1– точка разрыва 2 рода Пример 13. Исследовать функцию
Решение. Данная функция не определена в точках x = − 1 и x = 1. Следовательно, функция имеет разрывы в точках x = ± 1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.
Поскольку левосторонний предел при x = − 1 равен бесконечности, то данная точка является точкой разрыва второго рода.
Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.
Пример 14. Показать, что функция Решение:
также непрерывна при всех x за исключением точки x = 0. Так как то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию
которая будет непрерывной при любом действительном x. Пример 15. Найти точки разрыва функции Решение: Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется. Вычислим односторонние пределы при x = 0.
Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен
При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва. Пример 16. Найти точки разрыва функции Решение: Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке.
Видно, что в точке x = 0 существует разрыв первого рода
|
|||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.154 (0.007 с.) |
 lim f(x) =A и lim f(x) = B
lim f(x) =A и lim f(x) = B на непрерывность
на непрерывность

 имеет устранимый разрыв в точке x = 0.
имеет устранимый разрыв в точке x = 0.
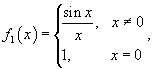
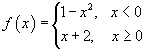 , если они существуют.
, если они существуют.
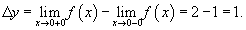
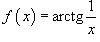 , если они существуют.
, если они существуют.



