
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изображение синусоидальных токов комплексными числамиСодержание книги
Поиск на нашем сайте
Любая синусоидальная функция может быть представлена на плоскости вращающимся вектором (рис. 1). Для расчёта цепей синусоидального тока векторы тока и напряжения изображают на комплексной плоскости и записывают в виде комплексных чисел. Принято на комплексной плоскости изображать векторы для момента времени w t=0. При этом мгновенное значение синусоидального тока
для момента времени w t =0 изображается вектором
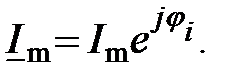
Величину Амплитуда Начальная фаза тока Примеры 1.1 Мгновенное значение синусоидального тока (или напряжения),
где
Здесь Если начальная фаза
Для функции с начальной фазой
комплексная амплитуда:
Переход от комплексных чисел к тригонометрическим формулам осуществляется в обратной последовательности. Например, комплексной амплитуде напряжения
соответствует мгновенное значение синусоидального напряжения
1.2 Комплексные действующие значения токов и напряжений В электротехнике принято применять не амплитуды, а действующие значения. Поэтому комплексную амплитуду нужно делить на
где Например, для комплексной амплитуды
комплексное действующее значение:
Переход от показательной формы комплексных чисел к алгебраической форме Применяются две формы комплексных чисел: 1) показательная, 2) алгебраическая. Переход осуществляется по формуле Эйлера
Например, комплексное действующее значение тока
в алгебраической форме записывается в виде
Вектор Положительные значения угла Если перед аргументом
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.18.103.165 (0.009 с.) |

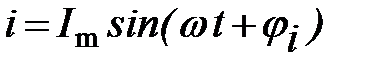
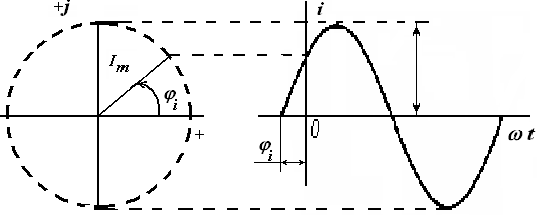
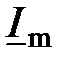 называют комплексной амплитудой тока (обозначают чертой снизу). Она характеризуется амплитудой
называют комплексной амплитудой тока (обозначают чертой снизу). Она характеризуется амплитудой  и начальной фазой тока
и начальной фазой тока 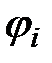 .
.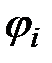 на комплексной плоскости представляет угол
на комплексной плоскости представляет угол  записывается в виде комплексной амплитуде по формуле
записывается в виде комплексной амплитуде по формуле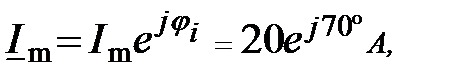
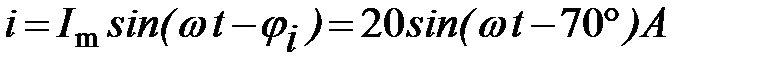 то и комплексная амплитуда записывается со знаком минус перед
то и комплексная амплитуда записывается со знаком минус перед 
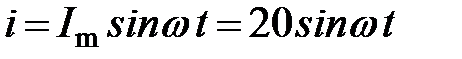
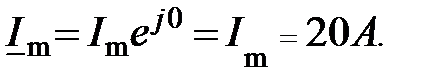
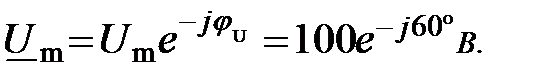
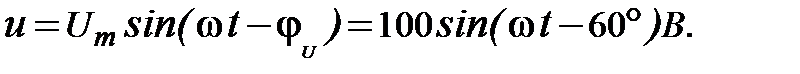
 :
: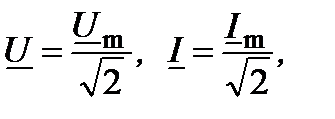
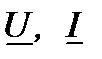 - комплексные действующие значения напряжения и тока.
- комплексные действующие значения напряжения и тока.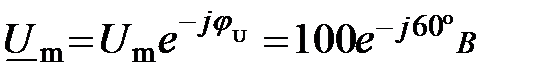
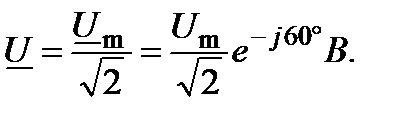
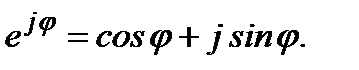
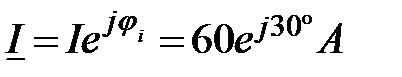 .
.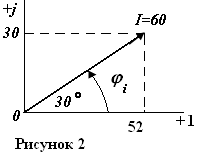
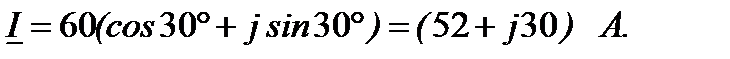
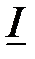 и его проекции на действительную и мнимую оси показаны на комплексной плоскости (рис.2). Длина вектора в масштабе равна его модулю I= 60 A. Угол
и его проекции на действительную и мнимую оси показаны на комплексной плоскости (рис.2). Длина вектора в масштабе равна его модулю I= 60 A. Угол 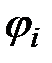 = 30° отсчитывается против направления вращения часовой стрелки, так как в формуле он имеет знак плюс.
= 30° отсчитывается против направления вращения часовой стрелки, так как в формуле он имеет знак плюс. отсчитываются от действительной оси против направления вращения часовой стрелки.
отсчитываются от действительной оси против направления вращения часовой стрелки.



