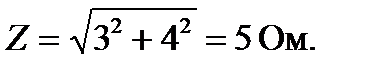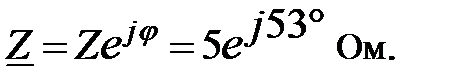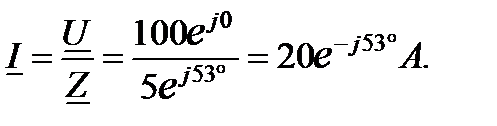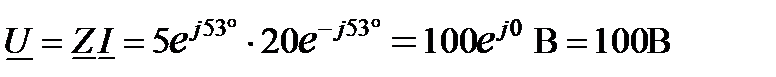Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переход от алгебраической формы к показательнойСодержание книги
Поиск на нашем сайте
Например, задано комплексное действующее значение напряжения в алгебраической форме
Требуется перевести его в показательную форму. Находим модуль (формула 1.75) и аргумент комплексного числа (формула 1.76). Модуль:
Аргумент:
В Величина
На рисунке 3 показаны вектор
Комплексное сопротивление Отношение называется комплексным сопротивлением.
Вычисление xL и xC Вычислить xL. L=25,4 мГ н, f = 50 Гц.
С=636 мкФ, f =50 Гц.
5. Вычислить Z при последовательном соединении R, XL, XC. 5.1 Вычислить
R= 160 Ом, xL= 10 Ом, xC= 130 Ом.
Переход к показательной форме:
Знак минус перед 5.2 Вычислить комплексное сопротивление ветви с резистором (рис.5). R= 2 Ом.
Исходим из формулы
Так как ветвь содержит только R, то XL=0 и XC=0. Следовательно,
5.3 Вычислить Задано xC= 5 Ом.
Так как R = 0, xL = 0, то комплексное сопротивление в алгебраической форме:
В показательной форме:
5.4 Вычислить
Так как R=0 и xC= 0, то комплексное сопротивление в алгебраической форме:
В показательной форме:
Сложение и вычитание комплексных величин Сложение и вычитание комплексных чисел проводится в алгебраической форме. Если числа заданы в показательной форме, то их следует перевести в алгебраическую форму. Например, требуется вычислить ток
По первому закону Кирхгофа:
Выразим токи в алгебраической форме:
Умножение и деление комплексных величин
Умножение и деление проще выполнять, если комплексные числа выразить в показательной форме.
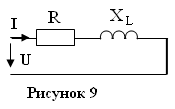
Например, требуется вычислить ток в цепи с активно-индуктивным сопротивлением (рис.9).
Начальная фаза напряжения не задана, следовательно, принимается
Сопротивление Модуль и аргумент
Как видно из формулы при делении комплексных чисел их аргументы вычитаются с учётом их знаков. При умножении аргументы складываются. Например,
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.01 с.) |

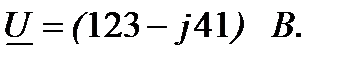
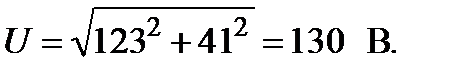
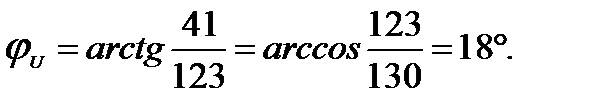
 входит отношение мнимой части комплексного числа к действительной, в
входит отношение мнимой части комплексного числа к действительной, в 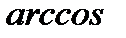 - отношение действительной части к модулю комплексного числа.
- отношение действительной части к модулю комплексного числа.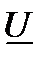 в показательной форме:
в показательной форме: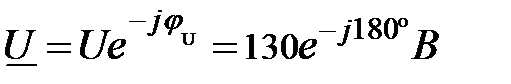 .
.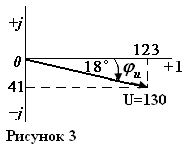 Знак минус перед аргументом
Знак минус перед аргументом 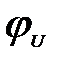 =18° обусловлен знаком перед мнимой частью числа
=18° обусловлен знаком перед мнимой частью числа 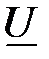 в алгебраической форме.
в алгебраической форме.
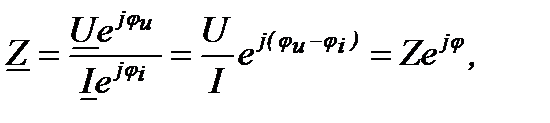
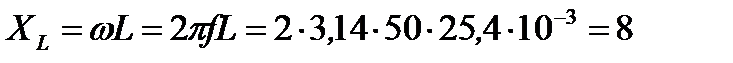 Ом
Ом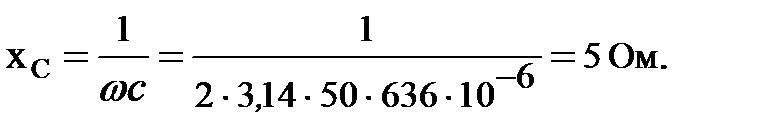
 ветви (рис.4).
ветви (рис.4).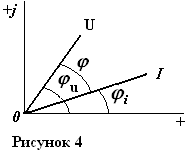
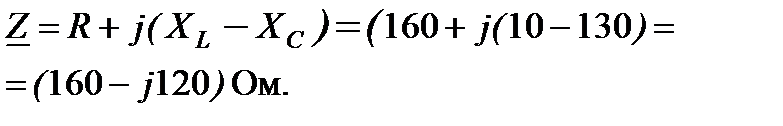
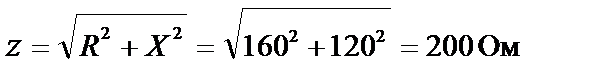 .
.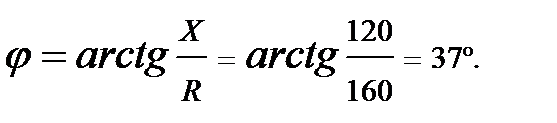
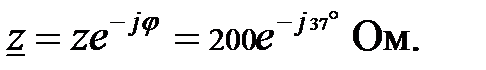
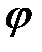 соответствует знаку минус перед мнимой частью в алгебраической форме числа
соответствует знаку минус перед мнимой частью в алгебраической форме числа  (_ указывает на емкостный характер сопротивления цепи).
(_ указывает на емкостный характер сопротивления цепи).
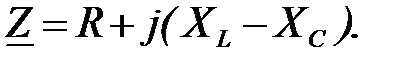
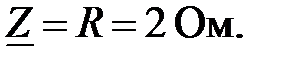
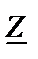 ветви с конденсатором (рис.6).
ветви с конденсатором (рис.6).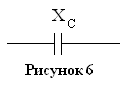
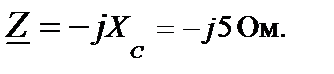
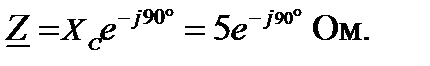
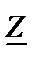 ветви с идеальной индуктивностью (рис.7). Задано xL= 8 Ом.
ветви с идеальной индуктивностью (рис.7). Задано xL= 8 Ом.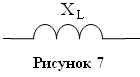
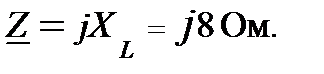
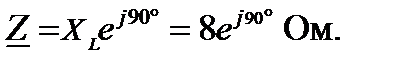
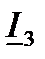 (рис.8). Токи
(рис.8). Токи 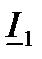 и
и 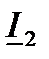 известны:
известны: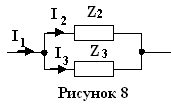
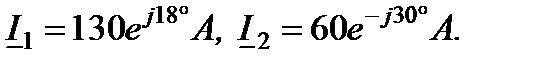
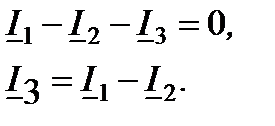
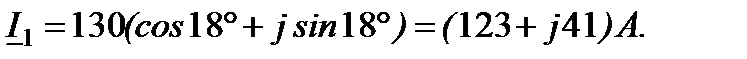
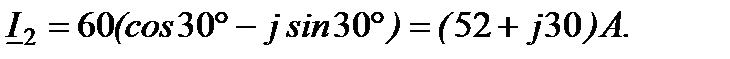
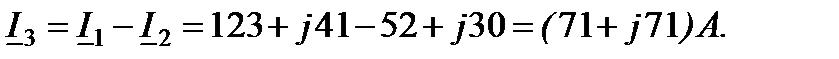 Модуль (действующее значение) и начальная фаза тока
Модуль (действующее значение) и начальная фаза тока 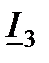 :
: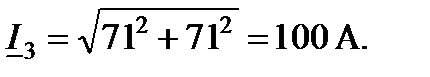
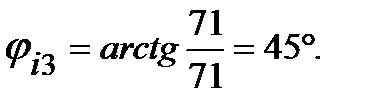
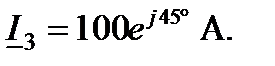
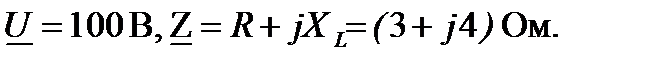
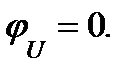
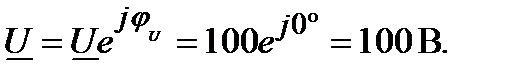
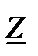 :
: