Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особые случаи применения симплекс - методаСодержание книги
Поиск на нашем сайте
Вырожденность. Если нет однозначной идентификации переменной (в случае одинаковых отношений), которая подлежит исключению из базиса, то выбор такой переменной можно сделать произвольно. Однако на следующей итерации по крайней мере, одна из базисных переменных должна быть равна нулю. В этом случае говорят, что новое решение является вырожденным. Появление вырожденного решения объясняется присутствием в модели, по крайней мере, одного избыточного ограничения. Пример 2. 9. 1: f0 = 3х1 + 9х2 ® maх
х1 + 2х2 + х4 = 4 (2) х i Таблица20
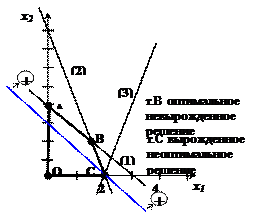
max f =18 при плане Х* = (0;2;0;0). Решим задачу графически. Через точку оптимума А проходят три прямые. Задача содержит только две переменные х1 и х2, поэтому для идентификации точки А достаточно 2-х прямых. Отсюда вывод: одно из ограничений является избыточным.
Рис. 20.
Информация, что некоторые ресурсы не нужны для достижения поставленной цели, оказывается полезной при практической реализации результатов исследования. Однако не существует надежных способов обнаружения избыточных ограничений непосредственно из симплекс - таблицы. Теоретически, вырожденность может привести к зацикливанию. Зацикливание. Посмотрите на симплекс – таблицу (см. табл. 20) значение целевой функции не улучшилось после 2-ой итерации по сравнению с 1 итерацией. Поэтому, можно предположить, что в общем случае может возникнуть зацикливание (циклическое повторение одинаковых операций, не улучшающих значение целевой функции, и не приводящих к завершению вычислительного процесса). Имеются специальные приемы, которые предотвращают зацикливание. Однако их использование чрезмерно замедляет процесс численных расчетов. Поэтому разработанные программы не содержат таких блоков, тем более, что вероятность зацикливания ничтожно мала. Пример 2. 9. 1. Появление промежуточного вырожденного решения. Рассмотрим пример.
n = 5; m = 3; (n - m)= 2 число небазисных переменных Таблица21
В рассмотренном примере на второй итерации вырожденности нет, причем значение целевой функции возросло с 6 до
Рис. 21.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.007 с.) |

 при ограничениях: х1 + 4х2 + х3 = 8 (1)
при ограничениях: х1 + 4х2 + х3 = 8 (1) 0, i = 1,..,4
0, i = 1,..,4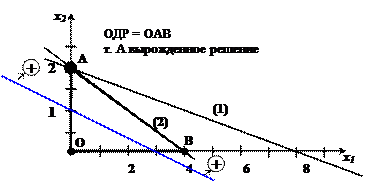
 4х1 + 3х2 £ 12 (1)
4х1 + 3х2 £ 12 (1)
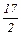 . Из примера можно сделать следующий вывод: итерации симплекс - метода должны выполняться до тех пор, пока не будет выполнено условие оптимальности! Точка С переопределена (через нее проходят 3 прямые).
. Из примера можно сделать следующий вывод: итерации симплекс - метода должны выполняться до тех пор, пока не будет выполнено условие оптимальности! Точка С переопределена (через нее проходят 3 прямые).