
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двойственная задача линейного программирования
С каждой задачей линейного программирования можно связать по определенному правилу другую задачу линейного программирования, которая называется двойственной. При этом исходную задачу называют прямой. Рассмотрение двойственной пары задач линейного программирования дает полезную дополнительную информацию о свойствах оптимального плана. Опишем способы построения двойственных задач и основные результаты теории двойственности. 1. Задача оптимального планирования производства. Как известно, эта задача формализуется как стандартная задача линейного программирования:
 
Напомним содержательный смысл параметров и переменных задачи: bi – общее количество ресурса Ri, aij – количество ресурса Ri, расходуемого на производство единицы продукта Pj, cj – прибыль от реализации единицы продукта Pj, xj – количество продукта Pj, планируемое к выпуску. Прямая задача: найти план выпуска продукции, обеспечивающий максимальную прибыль при заданных ограничениях на расход ресурсов. Для формулировки двойственной задачи будем учитывать ценность ресурсов. Предположим, что в рамках некоторого объединения предприятие реализует ресурсы другому предприятию. Первое предприятие оценивает свои ресурсы с точки зрения возможной прибыли от производимой продукции и условием продажи считает оценку ресурсов не меньшую, чем прибыль от готовой продукции. Второе предприятие имеет цель минимизировать стоимость приобретаемых ресурсов. В этой связи возникает двойственная задача: установить такие цены на ресурсы (внутри объединения), чтобы минимизировать их общую стоимость (интерес покупателя) при условии, чтобы стоимость расхода ресурсов на единицу продукта была не ниже соответствующей прибыли от реализации (интерес продавца). Проведем формализацию этой задачи. Пусть у i≥ 0, - планируемая цена (оценка) ресурса Ri, i= 1,…, m. Тогда общая стоимость ресурсов выражается величиной Стоимость ресурсов, необходимых для производства единицы продукта Pj, равна С учетом заявленных требований приходим к следующей задаче линейного программирования относительно переменных у1…..уm:
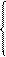 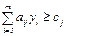
Это двойственная задача по отношению к прямой задаче (2.14). По существу, она является канонической задачей линейного программирования (как и прямая задача).
Двойственная задача - это вспомогательная задача линейного программирования, которая формулируется из исходной (прямой) задачи с помощью определенных правил.
Переменные прямой задачи.

Правила постановки двойственной задачи: 1) Каждому ограничению прямой задачи соответствует переменная двойственной задачи. 2) Каждой переменной прямой задачи соответствует ограничение двойственной задачи. 3) Коэффициенты а ij при некоторой переменной - xj фигурирующие в ограничениях прямой задачи, становится коэффициентами левой части соответствующего ограничения двойственной задачи, а соответствующий коэффициент c j в целевой функции прямой при той же переменной xj становится постоянной правой части ограничений двойственной задачи. Из правил следует, что двойственная задача имеет m переменных (у1,...,y m) и n ограничений, соответствующих n переменным прямой задачи. Рассмотрим, как формируются направление оптимизации, ограничения и знаки двойственных переменных. Таблица 42
Примеры формулировок двойственных задач. Пример 2. 12. 1:. Прямая задача. f 0 =5 × х1+12 × х2+4 × х3 → ma х при ограничениях:
2 × х1- - х2+3 × х3=8 х1, х2, х3 ≥ 0 В канонической форме прямая задача f0 = 5 × х1 + 12 × х2 + 4 × х3 + 0 × х4 ® m ах
2 × х1 - х2+3 × х3+ 0 × х4 =8 y 2 х i ≥ 0 i =1,2,..,4 Двойственная задача. W = 10 × y 1 + 8 × y 2 →min при ограничениях:
х2: + y 1 - y 2 ≥ 12 х3: y 1 +3 × y 2 ≥4 х4: y 1 +0 × y 2 ≥0 y 1 ≥0, y2 – не ограничена в знаке Пример 2. 12. 2: Прямая задача.
Двойственная задача. W = - 3 × y 1 + 5 × y 2 ® max при ограничениях
х2: - y 1 +3 × y 2 ≤-2 х3: y 1 ≤0 х4: y 2 ≤0 Пример 2. 12. 3: Прямая задача. f 0 =5 × х1 + 6 × х2 ® max
-х1+5 × х2 ≤ 3 4 × х1 +7 × х2 ≤ 8 х2≤ 0 х1 не ограничен в знаке Заменим х1=u-v, где u≥0, v≥0 Тогда f 0 =5 × u -5 × v + 6 × x 2 ® max
- u + v +5 × x2 –x3= 3 y2 4 × v-4 × v +7 × x2 +x4 = 8 y3; u, v, xi ³ 0, i =2, 3, 4 Двойственная задача. W = 5 × y 1 +3 × y 2 +8 × y 3 ® min при ограничениях
v: - y 1 + y 2 - 4 × y 3 ≥ - 5 или y 1 - y 2 +4 × y 3 ≤ 5 x 2: 2 × y 1 +5 × y 2 +7 × y 3 ≥6 x 3: - y 2 ≥ 0 x 4: y 3 ≥ 0 y 1 не ограничен в знаке.
Заметим, что ограничение двойственной задачи можно заменить одним ограничением в виде равенства y 1 –у2+4 × у3= 5. Такая замена возможна всякий раз, когда переменная прямой задачи не ограничена в знаке.
Пример 2. 12. 4: Прямая задача
Двойственная задача. W = 3 × y1 +5 × y2 ® max
х2: y 1 +3 × y 2 ≤ -2 х3: - y 1 ≤ 0 или y 1 ≥ 0 х4: y 2 ≤ 0 R: y 1 ≤ M т.е. y 1 ≥0, y 2 – не ограничена в знаке. Симметричная двойственная пара.
Представим задачи (1), (2) в векторно-матричной форме: <c,X>→мах, AX ≤ b, X ≥ 0, (2.16) <b,Y>→ min, ATy ≥ c, Y ≥ 0 (2.17)
Здесь AT – транспортированная матрица А. Отметим характерные структурные связи между задачами (2.16) и (2.17): 1) Число переменных двойственной задачи равно числу основных ограничений прямой задачи. 2) Матрица условий двойственной задачи равна транспортированной матрице условий прямой задачи. 3) Вектор ограничений прямой задачи является целевым вектором двойственной задачи и наоборот. 4) При переходе к двойственной задаче операция mах заменяется на min и меняется смысл неравенства в основных ограничениях.
Нетрудно видеть, что задача (2.16) является, в свою очередь, двойственной по отношению к задаче (2.17) (предварительно следует представить задачу (2.17) в канонической форме). Иными словами, задачи (2.16) и (2.17) взаимно двойственны. Назовем их симметричной двойственной парой задач линейного программирования. Установим простейшие свойства пары (2.16), (2.17). Введем множество допустимых планов. D = (X є Rn: AX ≤ b, X ≥ 0), Q = (Y є Rm: ATX ≥ c, Y ≥ 0). Лемма 1. Для любой пары допустимых планов X є D, Y є Q выполняется неравенство: <c,X> ≤ <b,Y>. Доказательство: Используя ограничения двойственной пары задач и свойства скалярного произведения, получаем: <c,X> ≤ <AT Y,X> = <y,AX> ≤ <b,Y>. Лемма доказана. Следствие 1. Если D≠Ǿ и целевая функция <c,X>не ограничена сверху на D, то Q≠Ǿ. Следствие 2. Если Q≠Ǿ и целевая функция <b,Y>не ограничена снизу на Q, то D≠Ǿ. Лемма 2. Пусть Xо є D, Yо є Q, причем <c,Xо>=<b,Yо>. Тогда Xо – решение прямой задачи, Yо – решение двойственной задачи.
Доказательство: На основании леммы 1 <c,X> ≤ <b,Yо> = <c,Xо> для всех X є D. Это означает, что Xо – решение прямой задачи. Аналогично, <b,Y> ≥ <c,Xо> = <b,Yо> для всех Y є Q, т.е. Yо - решение двойственной задачи. Лемма доказана. Лемма 3. Пусть в двойственной паре (2.16) и (2.17) допустимые множества не пусты: D≠Ǿ, Q≠Ǿ. Тогда прямая и двойственная задачи имеют решения. Доказательство:докажем разрешимость прямой задачи. Пусть Y є Q – допустимый план. Тогда <c,X> ≤ <b,Y> для всех X є D, т. е. целевая функция прямой задачи ограничена сверху на D. Отсюда на основании теории симплекс-метода заключаем, что прямая задача имеет решение. Аналогичные рассуждения проходят и для двойственной задачи. Лемма доказана. Несимметричная пара двойственных задач.
AX = b, (2.18) X ≥ 0 В векторно-матричной форме двойственная задача имеет вид: <b,Y> ® min, АуТ ³ с (2.19)
Задачу (2.19) называют двойственной по отношению к канонической задаче (2.18). Отметим, что в (2.19) нет условий неотрицательности и двойственные переменные неограниченны в знаке. Согласно построению значения задач (2.18), (2.19) совпадают, т. е. фактически доказана следующая теорема.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.110 (0.073 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

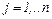

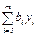 .
.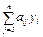 .
.
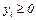


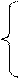
 Коэф. левых частей ограничений двойственной задачи
Коэф. левых частей ограничений двойственной задачи
 х1+2 × х2+х3≤10
х1+2 × х2+х3≤10 х1+2х2+х3+х4 = 10 y 1
х1+2х2+х3+х4 = 10 y 1 х1: y 1 +2 × y 2 ≥5
х1: y 1 +2 × y 2 ≥5 - х1+х2≥+3 × (-1) (1)
- х1+х2≥+3 × (-1) (1)
 х1 - х2+х3 = -3 y 1
х1 - х2+х3 = -3 y 1
 х1: y 1 +2 × y 2 ≤5
х1: y 1 +2 × y 2 ≤5
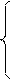 При ограничениях: х1 + 2 × х2 = 5
При ограничениях: х1 + 2 × х2 = 5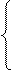 u - v + 2 × x2 = 5 y1
u - v + 2 × x2 = 5 y1 u: y 1 - y 2 +4 × y 3 ≥5
u: y 1 - y 2 +4 × y 3 ≥5 -х1+х2-х3+ R =3 y 1
-х1+х2-х3+ R =3 y 1
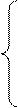 х1: - y 1 +2 × y 2 ≤ 5
х1: - y 1 +2 × y 2 ≤ 5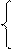 Рассмотрим задачу линейного программирования в канонической постановке: <c,X>® m ах,
Рассмотрим задачу линейного программирования в канонической постановке: <c,X>® m ах,


