Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифицированный геометрический методСодержание книги
Поиск на нашем сайте
Линия уровня целевой функции – линия, вдоль которой f сохраняет свое значение при переменных х1, х2. Для линейной функции (n=2) семейство линий уровня – семейство параллельных прямых. Из курса высшей математики известно, что градиент функции всегда перпендикулярен линии уровня f(x1,x2) =const и показывает направление возрастания функции f
Алгоритм метода: 1),2) Аналогично алгоритму графического метода. 3) Строим линию уровня целевой функции для произвольной константы. 4) Определяем направление градиента. 5) Перемещаем линию уровня параллельно самой себе вдоль ОДР по направлению градиента при поиске max целевой функции (при поиске min f по направлению антиградиента). Последняя точка касания линии уровня с ОДР и даст оптимальную вершину. 6) Рассчитать координаты оптимальной вершины.
Риc. 7. Решение задачи модифицированным графическим методом
Построим линию уровня для примера 2.3.1.
при х1=0, х2=20 х2=0, х1=11 Изобразим на линии уровня градиент, выбрав произвольную точку N.
По оси х1 откладываем 20, по оси х2 откладываем 11. И строим вектор grad f, как сумму двух векторов. Градиент направлен слева–направо вверх. По grad f продвигаем линию уровня параллельно самой себе до последней точки касания ОДР, т.е. в данном случае это точка В, она и будет оптимальна. Пример 2.4.1. Мясокомбинатвыпускает два вида продукции А1 и А2. Продукт А1 изготовляется с помощью механизма В1, продукт А2 с помощью механизма В2. Затем оба продукта упаковываются на специальном оборудовании. Производительность механизма В1 равна 4 т/ч, потери сырья при этом составляют 15%, суточная же производительность механизма В2 равна 3,5 т/ч, потери сырья достигают 20%. В течение суток механизмы В1 и В2 могут работать не более 18 час и 20 час соответственно; 1 час работы этих механизмов обходится мясокомбинату в 300 и 250 долларов. Специальное оборудование может работать не более 10 час. в сутки, упаковывая за 1 час 12 т продукта А1 или 10 т продукта А2. Один час его использования обходится мясокомбинату в 200 долл. Стоимость 1 кг сырья равна 3 долл. Упаковка продукта А1 весом 4/5 кг продается на рынке по 6 долл., упаковка же продукта А2 весом 3/5 кг – по 5 долл. Необходимо порекомендовать мясокомбинату такие суточные потребления сырья для производства продукции А1 и А2, при которых чистая прибыль была бы максимальной. Предполагается, что рынок сбыта для каждого вида продукции практически неограничен.
Рис. 8. Технологическая схема производства Математическая формулировка задачи Обозначим:
100% +15% в долях равна 1,15 – кол-во сырья для механизма В1, 100% + 20% в долях равна 1,2 – кол-во сырья для механизма В2, Чистая прибыль f равна доходу от продажи упаковок продуктов А1 и А2 за вычетом стоимости сырья и работы механизмов В1 и В2 и специального оборудования. Математическая модель:
х i≥0 i=1,2 или после несложных преобразований:
х2 ≤ 70 (2) 5 ×х1 + 6 ×х2 ≤ 600 (3) Находим отрезки, отсекаемые по осям координат прямой 5 ×х1 + 6 ×х2 =600 (ограничение 3): при х1 = 0, х2 = 100 при х2 = 0, х1 = 120
Рис.9. Графическое решение задачи Находим координаты вершин ОДР из решения системы прямых, образующих этих вершины. т. A (0,70); т. D (72,0) Координаты вершины С определяем из системы:
х1=72, отсюда С (72;40) Координаты вершины В находим из системы:
х1=70, отсюда В(36;70)
Рассчитаем значения целевой функции в вершинах: f(A)=3958,4 × 0+4642 × 70=324940 f(В)=3958,4 × 36+4642 × 70=467442,4 f(C)=3958,4 × 72+4642 × 40=470684,8 f(D)=3958,4 × 72+4642 × 0=285004,8 Получаем, что оптимальной вершиной будет С (72,40), то есть для получения максимальной прибыли на механизм В1 следует подать 1,15 ×72 =82,8 (т) сырья, на механизм В2 – 1,24 ×40= 48 (т) 2.5. Геометрический метод решения задач линейного программирования со многими переменными Геометрические соображения могут быть полезными при решении задач линейного программирования со многими переменными, а именно, когда в рассматриваемой задаче линейного программирования число переменных больше числа ограничений, записанных в форме равенств, не более чем на 2. Пусть, например, дана задача линейного программирования в следующей постановке. f (x) = на множестве X = { x где n – l = 2, причем ранг матрицы А = // a m+ i j // равен l. i = 1,…, l; j = 1,…, n Тогда, используя метод Жордана–Гаусса (метод исключения неизвестных), производим в системе ограничений-равенств
l исключений, в результате которых l =n – 2 переменных выразятся через оставшиеся две переменные, скажем через x1 и x2, т. е. x j= pj1 x1 + pj2 x2+ b i, j =3,4,…,n, (2.12) где pj 1, pj 2, b i - некоторые числа. Подставляя эти выражения в целевую функцию f и систему ограничений – неравенств
получаем уже задачу линейного программирования с двумя переменными:
на множестве Далее с помощью геометрических построений находим ее решение (x1*, x2*). Затем подставляем эти числа в (2.12) и (2.13), в результате получаем оптимальное решение и значение целевой функции исходной задачи (2.10) - (2.11). Описанный метод исключения переменных, конечно, применим и в том случае, если в задаче (2.10) - (2.11) n- l=1. Тогда все сводится к описанию решения элементарной задачи линейного программирования с одной переменной. Если в задаче (2.10) - (2.11) на все переменные xj, j= 1,…, n, наложено условие неотрицательности, то это приводит к уменьшению числа ограничений вида pj1 x1+ pj2 x2+ βj ≥ 0. Пример 2. 5. 1. На металлургическом заводе производится чугун из материала треx видов, отличающихся друг от друга содержанием серы, фосфора, марганца и стоимостью: Таблица 6
Остальные 5 % шиxтового материала каждого вида составляют другие компоненты. Определить оптимальный набор шиxтового материала, при котором можно получить с наименьшими затратами чугун, содержащий не менее 12 % серы, не более 28 % фосфора и не более 60 %марганца. Математическая формулировка задачи Обозначим через xj, j = 1, 2, 3, количество шиxтового материала вида А j,необxодимое для получения 1ед. чугуна. Тогда математическая модель приведенной задачи запишется в виде: минимизируется стоимость 1 ед. чугуна f (x) = 10 x1+ 15 x2 +12 x3 → min на множестве ограничений на содержание компонентов в чугуне
30 × x 1 + 25 × x2 + 17 × x3 50 × x 1 +60 × x2 + 70 × x3 x 1+ x2+ x3 = 1 xj ≥ 0, j = 1,2,3 Замечаем, что в данной модели число переменных равно n=3, и имеется ограничение – равенство, следовательно, n–1=2. Поэтому из имеющихся равенств выражаем одну переменную, например, x1=1-x2–x3≥0. Затем подставляем полученное значение переменной x1 в целевую функцию f(x) и в оставшиеся неравенства множества X. f(x)=10-10 ×х2-10 ×х3+15 ×х2+12 ×х3=10+5 ×х2+2 ×х3 х1=1-х2-х3
30-30 ×х2-30 ×х3+25 ×х2+17 ×х3 £ 28 или 5х2+13х3 ³ 2 50-50 ×х2-50 ×х3+60 ×х2+70 ×х3 £ 60 или 10х2+20х3 £10 х2+х3 £ 1 Последнее неравенство получено из условия, что х1 ³ 0. В результате получаем задачу линейного программирования уже с двумя переменными x2 и x3:
на множестве:
5 x2+13 x3 ³ 2 (2) x2+2 x3 £ 1 (3) x2+ x3 £ 1 (4) x 2 ³ 0; x 3 ³ 0
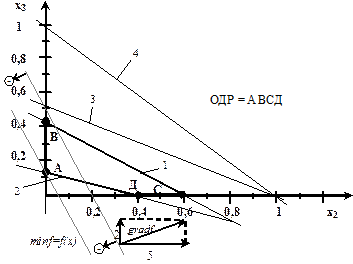
x2=0 Отсюда x2* = 0; x3* = 2/13, т.е. А (0;2/13), и минимальное значение функции f * =
Рис.10. Графическое решение задачи Определяем оставшуюся компоненту оптимального решения исходной задачи X* = (x 1*, x 2*, x 3*): x 1* = 1- x 2* - x 3* =1-0- Таким образом, для получения 1 ед. чугуна с наименьшей себестоимостью, равной
Пример 2. 5. 2. В течение квартала планируется выпуск двух видов продукции. Фирма может оплатить материалы и труд (себестоимость) из двух источников – собственных и заемных средств. Собственные средства фирмы составляют 30000$. Банк может ссудить до 20000$ под 5% с условием погашения ссуды в конце квартала. Производственные мощности фирмы, цены и себестоимость продукции содержатся в таблице: Таблица 7
Определить объемы выпуска продукции 1 и 2 и объем заемных средств, максимизирующих прибыль, если известно, что отношение объемов выпуска продукции 1 и 2 равно 2:1. Математическая формулировка задачи Обозначим через х i – количество продукции вида i (i=1,2), х3 – объём заёмных средств. Целевая функция: f (x) = (14 – 10) х1 + (11- 8) х2 – 1,05 х3= 4х1+3х2-1,05х3 → max.
10 х1 + 8 х2 ≤30 000+х3 (1) Величина заемных средств: х3 ≤ 20 000 (2) Производственные ограничения (в часах): 0,5 х1 + 0,3 х1 ≤ 540 (3) 0,3 х1 + 0,4 х2 ≤ 500 (4) 0,2 х1 + 0,1 х2 ≤ 350 (5) Объемы выпуска х1 = 2 х2 (6) х i ≥ 0, i=1,2,3 С учетом ограничения х1=2х2 придем к задаче с двумя неизвестными: f (x) = 4х1+3х2–1,05х3=4 ×2х2+3х2–1,05х3= 11х2–1,05 х3 → max.
при х3=0 х2=1071,4 х3 ≤ 20000 (2) х3=20000 1,3х3 ≤ 540 (3) х3=415,4 х2 ≤ 500 (4) х2=500 0,5х2 ≤ 350 (5) х2=700 х i ≥ 0, i=2,3 В целевой функции коэффициент при х3 отрицательный, требуется max прибыль, т.е. в оптимальном решении х3=0. При х3=0, достигается max прибыль в т.А (рис.11)
х2*=415,4 х3*=0 max f (х*)= 11. 415,4-1,05. 0=4569,4
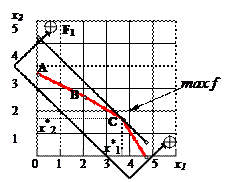
Рис.11. Графическое решение задачи Пример 2. 5. 3. Менеджер желает приобрести акции трех ведущих предприятий, которые могут дать месячный доход, равный соответственно 11%, 15% и 8%. Риски при вложении капитала для приобретения данных акций определены рынком и равны соответственно 1; 1,2; 0,9. Требуется, чтобы средняя взвешенная этих рисков была не более 1,1. Менеджеру необходимо определить такие доли вложения своего капитала при покупке акций, которые приведут к получениию максимального дохода. Математическая формулировка задачи Обозначим: х i – количество акций i –го предприятия; р i - вероятность получения дохода; Математическое ожидание месячного дохода f: f=
x1+1,2x2+0,9x3 £ 1,1 (2) xi ³ 0 i=1,...,3 Выразим из (1) х1=1-х2-х3 ³0. Тогда f(x)=11-11 x1-11 x3+15 x2+8 x3=11+4 x2-3 x3 ® max Так как коэффициент при х3 отрицательный, то в оптимальном решении х3=0. Убедимся в этом решив задачу графическим методом (рис.12) Так как х1 ³0, то получим: 1-х2-х3 ³ 0 Þ
1-х2-х3+1,2х2+0,9х3 £ 1,1 или 0,2х2-0,1х3 £ 0,1 (2) х2, х3³0 max f = f(C), т.е. оптимальный доход достигается в точке С с координатами (0,5;0). Тогда f(C)= 11+4. 0,5 – 3. 0 = 13, оптимальный план Х*= (0,5;0,5;0).
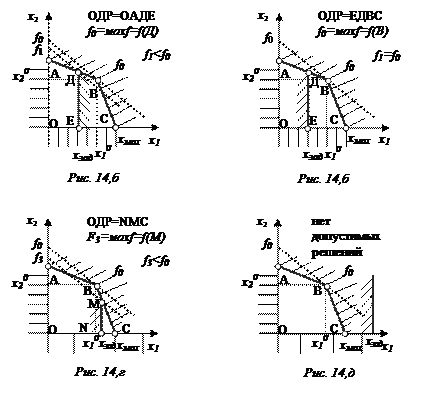
Рис. 12. Графическое решение задачи Виды оптимальных решений Тот факт, что оптимальное решение находится в вершине ОДР, дал нам возможность сформулировать метод решения задач линейного программирования. Но из этого же факта можно сделать еще два очень важных вывода. Во-первых, если оптимальным решением являются координаты вершины ОДР, значит, столько оптимальных решений может иметь задача. Во-вторых, поскольку чем больше ограничений, тем больше вершин, то, следовательно, чем больше ограничений, тем больше оптимальных решений. Как видно из рис.14.а, вершина, координаты которой являются оптимальным решением, определяется углом наклона прямой, описывающей целевую функцию. Значит, каждая вершина будет соответствовать оптимальному решению для некоторой целевой функции.
Рис. 13 Поясним это на примере. Пусть для двух видов продукции П1 и П2 требуются трудовые, материальные, финансовые ресурсы. Наличие ресурсов каждого вида и их нормы расхода, необходимые для выпуска единицы продукции, приведены в табл.8. Таблица 8
Составим математическую модель задачи. Ограничения и граничные условия, входящие в модель этой задачи, будут иметь вид:
3 × х1+4 × х2 £ 18; 6 × х1+2 × х2 £ 27; х1 ³ 0; х2 ³ 0; Найдем оптимальные решения для пяти целевых функций: максимизация суммарного выпуска f 1 = х1+ х2 максимизация выпуска продукции П2 f 2 = х2 максимизация выпуска продукции П1 f 3 = х1 максимизация прибыли f 4 =4 х1+8,5 х2 минимизация используемых ресурсов f 5 =(1+3+6) × х1+(4+4+2) х2 т.е. f5=10 х1+10 х2 Для каждой приведенной целевой функции можно построить линию целевой функции и определить вершину, в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведены в таблицу 9, из анализа которой можно сделать вывод: координаты каждой вершины могут быть оптимальным решением задачи в некотором принятом смысле. Так, вершина С дает максимальный суммарный выпуск, вершина А – максимальный выпуск продукции П2 и т.д. Таблица 9
Рассмотрим далее, как влияет на оптимальное решение введение дополнительных ограничений. Пусть дана задача, которая графически представлена на рис 14,а
Рис. 14,а Принимаем, что при максимизации оптимальное решение находится в вершине В и имеет значения х10, х20, f0. Рассмотрим, как влияют на оптимальное решение дополнительные ограничения, например, применительно к х1. Таблица 10
Из рис 14 и табл.10 видно следующее: дополнительное ограничение ухудшило целевую функцию (рис 14,б), оптимальное решение не изменилось (рис 14,в), оптимальное решение ухудшилось (рис 14,г), характерно появились несовместности (рис 14,д), которое привело к тому, что задача вообще не имеет решения. Подытоживая влияние дополнительных ограничений на оптимальное решение, можно отметить три варианта: дополнительное ограничение не влияет на значение целевой функции, ухудшает ее, создает несовместность, т.е. исключает возможность получения даже допустимого решения. Можно сформулировать еще короче: дополнительное ограничение никогда не улучшает оптимального решения. Значит, если мы хотим улучшать принятую целевую функцию, т.е. результат работы, мы должны стремиться к тому, чтобы иметь как можно меньше ограничений. 2.7. Основы анализа модели на чувствительность Анализ моделей на чувствительность - это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. При таком анализе всегда рассматривается некоторая совокупность линейных оптимизационных моделей, то есть по существу, некоторая модель исследования операций. Это придает модели определенную динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Для проведения анализа будем использовать графический метод. Пример 2.7.1. Небольшая фабрика одной из фирм изготавливает два вида красок: для внутренних (I) и для наружных (E) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта A и B. Максимально возможные суточные запасы этих продуктов составляют 6 т и 8 т соответственно. Расходы продуктов A и B на 1 т соответствующих красок приведены в таблице:
Таблица11
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску E более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Какое количество краски вида E и I должна производить фабрика, чтобы доход от реализации продукции был максимальным? Обозначим: х E - суточный объем производства краски E (т). х I - суточный объем производства краски I (т). При допущении независимости объемов сбыта каждой из красок общий доход f0 равен сумме двух слагаемых 3х E + 2х I. В целом математическая модель f0=3х E+2х I ® max
2х E+х I £ 8 (2)- на расход продукта В х I -х E £ 1 (3)- соотношение спросов на краски х I £ 2 (4)- спрос на краску I х I ³ 0; х E ³ 0
Данная математическая модель является линейной, так как целевая функция f0 и все ограничения линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности. Пропорциональность ‑ означает, что вклад каждой переменной х I и х E в целевую функцию f0 и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной. Если, например, фирма будет предоставлять потребителям скидку, продавая краску E по 2, 5 тыс. долларов за тонну при объеме закупок свыше 2 тонн, то в этом случае прямой пропорциональности между доходом фирмы и величиной х E нет.
Рис. 15. Аддитивность - заключается в том, что каждая целевая функция представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое будет пропорционально величине соответствующей переменной. Если, например, фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности. На рис.15 данная задача решена графическим методом. Максимальное значение прибыли достигается в вершине D при плане выпуска: хЕ = max f = 12 Первая задача анализа на чувствительность Позволяет определить статус ресурсов и допустимые пределы изменения ресурсов. Классифицируем ограничения линейной модели как связывающие (активные) и не связывающие (неактивные) ограничения. Прямая, представляющая активное ограничение, должна проходить через оптимальную вершину. Вернемся к рассмотренному примеру о фирме, выпускающей краски Е и I. В нашем примере связывающие ограничения (1) и (2), они лимитируют запасы исходных продуктов (ресурсов) А и В. Если ограничение является связывающим, то логично отнести соответствующий ресурс к разряду дефицитных ресурсов, так как он используется полностью. Ресурс, с которым ассоциировано несвязывающее ограничение, следует отнести к разряду не дефицитных ресурсов, потому что часть этого ресурса остается неиспользованной. При анализе модели на чувствительность по правым частям ограничений определяют: 1) предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение max f0; 2) предельно допустимое снижение запаса недефицитного ресурса, не изменяющее max f0. Информация по пункту 2 может быть полезна в тех случаях, когда излишки не дефицитных ресурсов могут быть использованы для других целей. Может возникнуть вопрос: не следует ли проанализировать, как повлияет на оптимум: 1. увеличение объема ресурсов, имеющихся в избытке. 2. сокращение объема дефицитных ресурсов. Ответ на первый пункт очевиден, т.е. в этом случае мы сделаем избыточный ресурс еще более избыточным, что никак не повлияет на полученное ранее решение. По второму пункту покажем, что сокращение дефицитного ресурса никогда не улучшает значение целевой функции. На рис. 16 нарисуем ограничение х E+2х I £ 4. В этом случае оптимальной является (1¢) вершина N, координаты вершины определяют из совместного решения:
2х E+х I = 8 8- 4х I+х I=8 х I( N)= 0 f0(N)=12, то есть оптимальное значение целевой функции уменьшилось с уменьшением запаса дефицитного ресурса (продукта А). Рассмотрим теперь увеличение ресурса А, при этом прямая (1) (или отрезок СД) переместится вверх параллельно самой себе. Имеет смысл увеличить запас продукта так, чтобы прямая (1) прошла через вершину К. Большее увеличение продукта А приведет к тому, что ресурс (1) станет избыточным. В точке К ограничения (2) и (4) становятся связывающими. Оптимальное решение при этом достигается в вершине К, а ОДР становится многоугольник ОАВКЕ. Координаты вершины К:
х I=2 (4) х E= f0(К)= 3 ×х E+2 ×х I = 3 ×3+2 ×2= 9+4 =13. Для определения предельного запаса ресурса А следует координаты вершины К подставить в левую часть ограничения (1). Тогда новое значение запаса продукта А равно: х E+2 ×х I=3+2 ×2=7, т.е. следует увеличить запас продукта А на D1=7-6=1 (т), где 6 – это старое значение запаса продукта А.
Рис. 16. Рассмотрим вопрос о целесообразности увеличения запаса дефицитного ресурса (2) (исходный продукт В). Запас продукта В следует увеличить так, чтобы прямая (2) прошла через вершину N. Новой оптимальной вершиной становится точка N, где пересекаются прямая (1) и ось абсцисс (х I=0) тогда
х I=0 х E=6 f(N)= f(6;0)=18 Для нахождения величины запаса продукта В, который гарантирует прибыль f=18 тыс.$, подставим координаты вершины N в ограничение (2): 2х E( N)+ х I( N)=2 ×6=12. Тогда абсолютный прирост запаса продукта В: D 2=12-8=4 (т) Рассмотрим теперь вопрос об уменьшении правой части несвязывающих ограничений. Ограничение (4) (отрезок ВС) опускаем вниз до пересечения с оптимальной вершиной Д, так как координаты точки Д: х E(Д)=3 то уменьшение спроса на краску I до величины хI(Д)= Сокращение спроса: D 4= (знак ¢-¢ свидетельствует об уменьшении запаса ресурса). Сокращение спроса адекватно уменьшению представительства на рынке, посредством которого реализуется краска вида I. Рассмотрим ограничение (3), х E+х I £ 1, которое представляет соотношение между спросом на краску I и спросом на краску Е. И в этом случае правую часть огранич
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.130.228 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

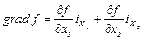 , где
, где 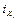 ,
, 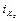 – единичные орты, ориентированные вдоль соответствующих осей.
– единичные орты, ориентированные вдоль соответствующих осей.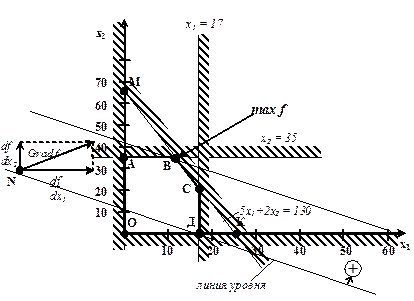
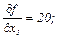
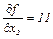
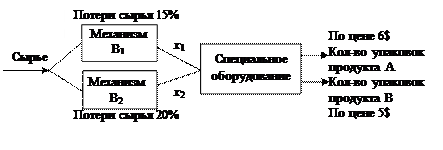
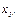
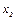 (т) – количество продукта А1 и А2 соответственно;
(т) – количество продукта А1 и А2 соответственно;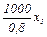 – количество упаковок продукта вида А1;
– количество упаковок продукта вида А1;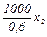 – количество упаковок продукта вида А2;
– количество упаковок продукта вида А2;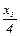 – время работы механизма В1;
– время работы механизма В1; 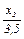 – время работы механизма В2.
– время работы механизма В2.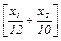 - время работы специального оборудования.
- время работы специального оборудования.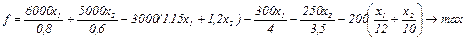 при ограничениях:
при ограничениях: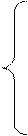
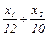 ≤ 10 (3)
≤ 10 (3) х1 ≤ 72 (1)
х1 ≤ 72 (1)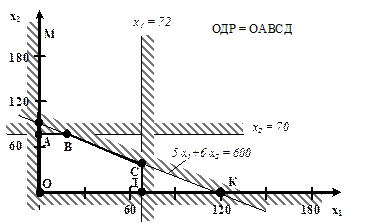
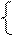 5 ×х1 + 6 ×х2 ≤ 600
5 ×х1 + 6 ×х2 ≤ 600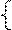 5 ×х1 + 6 ×х2 ≤ 600
5 ×х1 + 6 ×х2 ≤ 600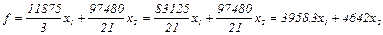
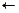 max f
max f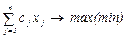 (2.10)
(2.10)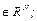
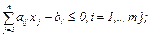
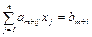 , i = 1,…, l; x j
, i = 1,…, l; x j 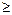 0, j = 1,…, n.}, (2.11)
0, j = 1,…, n.}, (2.11)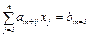 , i = 1,…,l,
, i = 1,…,l,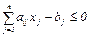 , i = 1,…, m,
, i = 1,…, m,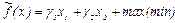 (2.13)
(2.13)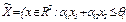 , i =1,…, m; pj1 x1+ pj2 x2 + βj ≥ 0, j=3,4,…, n; x1≥ 0, x2≥ 0.}, где α i1 , α i2, θ i (i = 1,…, m), γ1, γ2, δ – некоторые числа.
, i =1,…, m; pj1 x1+ pj2 x2 + βj ≥ 0, j=3,4,…, n; x1≥ 0, x2≥ 0.}, где α i1 , α i2, θ i (i = 1,…, m), γ1, γ2, δ – некоторые числа.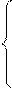 15 × x 1 +10 × x2+ 8 × x3 ≥ 12
15 × x 1 +10 × x2+ 8 × x3 ≥ 12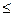 28
28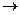 min
min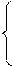 15-15 ×х2-15 ×х3+10 ×х2+8 ×х3 ³ 12 или 5х2+7х3 £ 3
15-15 ×х2-15 ×х3+10 ×х2+8 ×х3 ³ 12 или 5х2+7х3 £ 3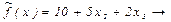 min
min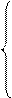 5 x2+7 x3 £ 3 (1)
5 x2+7 x3 £ 3 (1)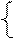 Построим допустимое множество и линии уровня целевой функции
Построим допустимое множество и линии уровня целевой функции 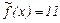 в системе координат x2 x3 (рис10). На рисунке видно, что линейная функция принимает минимальное значение в вершине А ОДР ABCD. Координаты этой вершины отыскиваем, решая систему уравнений граничных прямых 5 x2+13 x3 =2
в системе координат x2 x3 (рис10). На рисунке видно, что линейная функция принимает минимальное значение в вершине А ОДР ABCD. Координаты этой вершины отыскиваем, решая систему уравнений граничных прямых 5 x2+13 x3 =2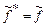 (x2*; x3*)= 10+5 ×0+2 ×
(x2*; x3*)= 10+5 ×0+2 × 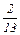 =
= 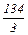 ($)
($) 
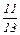
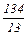 долл., необходимо использовать
долл., необходимо использовать  14% серы;
14% серы;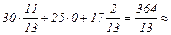 28% фосфора;
28% фосфора; 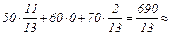 53% марганца.
53% марганца.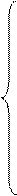 Затраты на материалы и труд:
Затраты на материалы и труд: 28х2–х3 ≤ 30000 (1) при х2=0 х3=-30000;
28х2–х3 ≤ 30000 (1) при х2=0 х3=-30000; х1*=830,8
х1*=830,8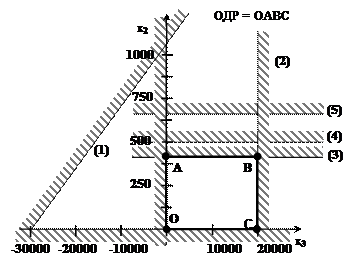
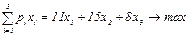
 x1+x2+x3=1 (1)
x1+x2+x3=1 (1)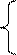 х2+х3 £ 1 (1)
х2+х3 £ 1 (1)
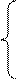 х1+4 × х2 £ 14;
х1+4 × х2 £ 14;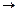 ma х
ma х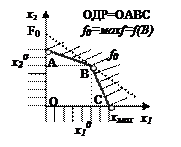
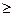 х зад
х зад
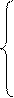 при ограничениях: х E +2х I £ 6 (1)- на расход продукта А
при ограничениях: х E +2х I £ 6 (1)- на расход продукта А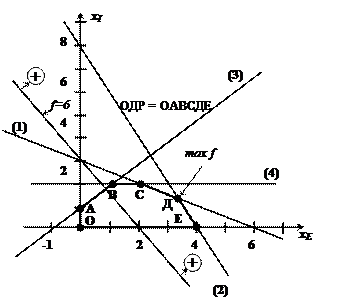
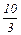 (т) и хI =
(т) и хI = 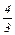 (т),
(т),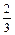 тыс.$
тыс.$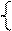 х E+2х I = 4 х E=4‑2х I хЕ( N)=4
х E+2х I = 4 х E=4‑2х I хЕ( N)=4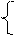 2 ×х E+х I=8 (2)
2 ×х E+х I=8 (2)  =3 Þ К(3;2)
=3 Þ К(3;2)
 х E+2х I=6
х E+2х I=6 ; х I(Д)=1
; х I(Д)=1 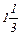 никак не повлияет на оптимальность ранее полученного решения.
никак не повлияет на оптимальность ранее полученного решения.