Классификация математических моделей

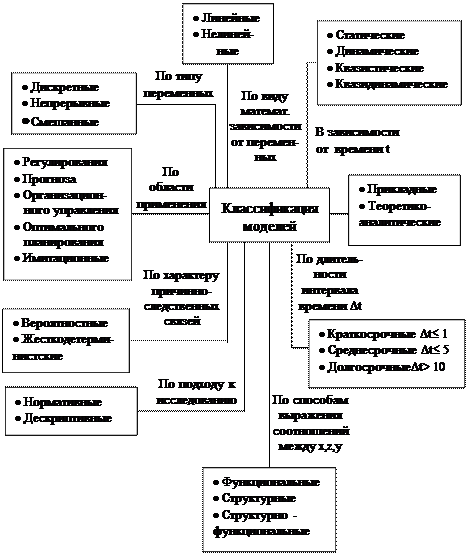
Математическая модель любого объекта (процесса, явления) включает три группы элементов.

1. Характеристики объекта, которые нужно определить:

                                                       Y = {y₁, y₂,..., y_n};

2. Характеристики внешних условий:

                                                       X = {x₁, x₂,..., x _m };

3. Совокупность внутренних параметров объекта:

                                                                    Z = {z₁, z₂,..., z _k }.

Множество условий Х и параметров Z могут рассматриваться как экзогенные величины (определяемые вне модели), а вектор Y определяет эндогенные величины, рассчитываемые с помощью модели.

Математическую модель можно интерпретировать как особый преобразователь внешних условий Х (вход объекта) в искомые характеристики Y (выход объекта).

По способам выражения соотношений между X, Z и Y модели делятся два основных вида структурные и функциональные.

Структурные модели отражают внутреннюю организацию объекта, его составные части, связи с входом и выходом и т. д.

Существует три вида структурных моделей:

1) Все неизвестные Y _j выражаются в виде явных функций от внешних условий (X) и внутренних параметров объекта (Z)

Y_j = f_j (X, Z),   где j =1,2,.. n                           (1.1);

2) Неизвестные Y _j определяются из решения системы известных соотношений (неравенств, уравнений и т. д.) вида

G_j (X, Z, Y) = 0,   где j =1,2,.. n                       (1.2);

3) Модель включает соотношения вида (1.2), но конкретный вид этих соотношений неизвестен. Модель как бы недостроена, определен только ее каркас.

Структурные модели (1.1) и (1.2) - это вполне определенные математические задачи, которые можно решать аналитическими или численными методами.

Структурные модели третьего типа возникают при попытках математического описания сложных систем, например, экономических или экологических. Для их исследования используются сравнительно новые математические дисциплины: исследование операций, теории случайных процессов, игр и статистических решений, массового обслуживания и т. д. Кроме того, активную роль в процессе разработки моделей этого вида играет ЭВМ. Совокупность подходов и методов к исследованию моделей рассматриваемого типа объединяется термином имитационное моделирование. Модели этого вида занимают промежуточное место между структурными и функциональными моделями.

Основная идея функциональных моделей - познание сущности объекта через важнейшие проявления этой сущности: деятельность, функционирование, поведение. Внутренняя структура объекта при этом не изучается. Объект, изучаемый посредствам функциональной модели, абстрактно можно представить в виде "черного ящика", внутренняя структура которого совершенно не видна. Функциональная модель имитирует поведение объекта так, что, задавая значения ”входа" X можно получать значения "выхода" Y.

Y = D (X)                                                           (1.3)

Построить функциональную модель - это значит, отыскать оператор D, преобразующий X в Y. Функциональные модели используются в экономическом регулировании.

Классификацию экономико-математических моделей можно производить по различным признакам (рис. 2).

Теоретико-аналитические экономико-математические модели используются при исследовании общих закономерностей и свойств экономических процессов.

Прикладные экономико-математические модели применяются для решения конкретных экономических задач (модели экономического анализа, прогнозирования, управления).

Для пассивного прогноза используются дескриптивные модели, которые объясняют наблюдаемые факты, отвечая на вопросы: «Как это происходит. Как это может развиваться дальше». Применение дескриптивного подхода в моделировании объясняется необходимостью эмпирического (экспериментального) выявления различных факторов, изучение вероятных путей в развитии. Когда знаний не хватает, то целесообразно умение искусственно воспроизводить (имитировать) экономический процесс. Примерами дескриптивных моделей являются некоторые виды производственных функций и функций покупательского спроса.

Нормативные модели отвечают на вопрос: «Как это должно быть», т.е. предполагают целенаправленную деятельность. Типичным примером нормативной модели является модель оптимального планирования.

 

 

 

 

Рис. 2. Классификация экономико-математических моделей

1.4. Этапы исследования экономических процессов

При постановке задач организационного управления важно:

1.Определить цель, преследуемую субъектом управления.

2.Установить, значения, каких переменных можно варьировать.

3.Определить, в каких пределах можно изменять эти переменные, т.е. определить допустимое множество значений управляемых переменных.

Под целью (критерием оптимальности, целевой функцией) будем понимать тот конечный результат, который необходимо получить путем выбора и реализации тех или иных управляющих воздействий на исследуемую систему. Другими словами, целевая функция - это количественная мера оценки качества принимаемого решения.

Процесс выработки наилучших решений называется оптимизацией.

Чтобы задача имела оптимальное решение, она должна удовлетворять двум требованиям:

· Должен существовать выбор возможных решений.

Если решение задачи одно, то нет никакого выбора, как нет и оптимизации.

· Необходимо принять критерий оптимальности.

В производственно - коммерческой сфере цель, как правило, заключается в том, чтобы максимизировать прибыль либо минимизировать отходы. В сфере некоммерческих услуг, например, в здравоохранении, стремятся к достижению высокого уровня обслуживания. Однако эта цель не может рассматриваться вне связи с соответствующими эксплуатационными расходами.

Помимо выявления индивидуальных целей необходимо правильно выбрать общую цель, приемлемую подавляющим большинством заинтересованных лиц. Так, например, рассмотрим отделы промышленной фирмы: производственный и сбыта. Имея одну общую цель (увеличения прибыли), отдел сбыта стремится к увеличению уровня складских запасов, чтобы в любое время можно было удовлетворить спрос. В тоже время, производственный отдел стремится к снижению текущего уровня складских запасов, так как из-за полной загруженности складских помещений выпускаемую продукцию придется хранить в производственных помещениях. Удовлетворить эти противоречивые требования обоих отделов невозможно, поэтому встает вопрос о компромиссном варианте, который бы наиболее отвечал интересам фирмы в целом. Многие задачи вообще не удается охарактеризовать единственной целевой функцией. Тогда в оптимизационной задаче появляется несколько разнородных критериев (многокритериальные задачи).

Чтобы решить задачу математическими методами, необходимо произвести формализационную постановку задачи, т.е. представить целевую функцию и ограничения в аналитическом виде. Несмотря на большое число переменных, и ограничений, лишь небольшая их часть может оказаться существенной для описания системы. Поэтому следует учитывать только доминирующие переменные и ограничения.

Можно выделить следующие этапы исследования экономических систем:

1.Идентификация проблемы.

Формулировка задачи и цели исследования. Выявление возможных альтернативных решений. Определение условий и ограничений для системы.

2. Построение модели.

Разработчик, учитывая особенность постановки задачи, должен выбрать модель, которая наиболее подходит для адекватного описания исследуемой системы. Должны быть установлены количественные соотношения для выражения целевой функции и ограничений в виде функций от управляемых переменных.

3.Решение задачи одним из математических методов.

Метод выбирается в зависимости от вида целевой функции. В случае имитационных или эвристических моделей получаемое решение соответствует лишь приближенным оценкам критериев оптимальности функционирования системы.

Кроме нахождения оптимального решения, если возможно, получают дополнительную информацию о возможных изменениях решения при изменении параметров системы. Эту часть исследования называют анализом модели начувствительность.

4.Проверка адекватности модели.

Модель считается адекватной, если несмотря на некоторые неточности отображения системы - оригинала она способна обеспечить достаточно надежное предсказания поведения системы.

Общий метод проверки адекватности состоит в сопоставлении получаемых результатов с характеристиками системы, которые имели место в прошлом. Если при аналогичных входных параметрах модель достаточно точно воспроизводит поведение системы, то она считается адекватной. Однако такое сопоставление не дает полной уверенности в том, что поведение системы в будущем такое же, как в прошлом.

Рассмотренный способ оценки адекватности модели непригоден при разработке новых систем. В этом случае обычно параллельно разрабатывается имитационная модель, предназначенная для получения данных, требуемых для проверки адекватности основной математической модели. Проверку пригодности прогнозных моделей можно свести к статистической проверке гипотез.

5. Реализация результатов исследования.

Результаты исследования оформляются в виде детальных инструкций для людей, которые обеспечивают управление системы и ее функционирование.